python假设检验实战，是否服从正态分布，异常数据，相关性

1.要解决的问题

给出的数据集为人体的体温数据，下载链接为 https://pan.baidu.com/s/1t4SKF6U2yyjT365FaE692A*

包括三个数据字段：

• gender：性别，1为男性，2为女性
• Temperature:体温
• HeartRate：心率

要解决的问题如下：

• 人体体温的总体均值是否为98.6华氏度？
• 人体的温度是否服从正态分布?
• 人体体温中存在的异常数据是哪些？
• 男女体温是否存在明显差异？
• 体温与心率间的相关性(强？弱？中等?)

首先导入数据集：

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from scipy import stats
data = pd.read_csv('test.csv')
temp = data['Temperature']
gender = data['Gender']
heartRate = data['HeartRate']

查看该数据集的各项数据

data.describe()

输出：

	Temperature	Gender	HeartRate
count	130.000000	130.000000	130.000000
mean	98.249231	1.500000	73.761538
std	0.733183	0.501934	7.062077
min	96.300000	1.000000	57.000000
25%	97.800000	1.000000	69.000000
50%	98.300000	1.500000	74.000000
75%	98.700000	2.000000	79.000000
max	100.800000	2.000000	89.000000

输入：

data.shape

输出：

(130, 3)

问题一：人体体温的总体均值是否为98.6华氏度？

这是一个正态总体，方差未知，均值的假设检验问题，使用的是 t 分布

$T=\frac{\bar{X}-{\mu }_0}{S/\sqrt{n}}$

$|T|\ge t_{\alpha /2}(n-1)$

原假设H0：$\bar{x}$=98.6

备择假设H1：$\bar{x}$!=98.6

设置默认显著性水平为 0.05

def hypothesis_mean(data, total_mean, alpha=0.05):
    sample_mean = np.mean(data)
    sample_std = np.std(data, ddof=1)
    sample_size = len(data)
    # 检验统计量
    t = (total_mean - sample_mean) * np.sqrt(sample_size) / sample_std
    t_score = stats.t.isf(alpha / 2, df = (sample_size-1) )
    if (t > t_score) or (t < -t_score):
        return True
    return False

if hypothesis_mean(temp, 98.6):
    print('接受H0，人体体温的总体均值为98.6华氏度')

接受H0，人体体温的总体均值为98.6华氏度

问题二：人体的温度是否服从正态分布?

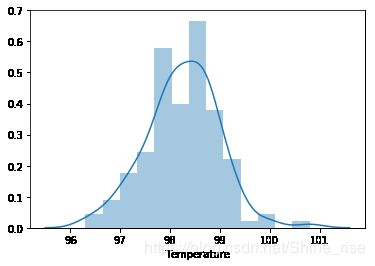
画出热度图，肉眼观察人体温度看是否服从正态分布。

根据中心极限定理，一般情况下，当数据量大于30的时候，可以近似看做服从正态分布，该数据集一共有130条数据，可以近似看做服从正态分布

sns.distplot(temp)

下面检验人体的温度是否服从正态分布

scipy.stats.normaltest 可以专门用作检验是否服从正态分布

方法：scipy.stats.normaltest (a, axis=0)

参数：

• a - 待检验数据；
• axis - 默认为0，表示在0轴上检验，即对数据的每一行做正态性检验，我们可以设置为 axis=None 来对整个数据做检验

返回：

• statistic - 统计量
• pvalue - p值，p大于0.05时，接受原假设H0，即H0为真，p小于0.05时，拒绝H0，即H0为假，接受H1

scipy.stats.normaltest(temp)

输出：

NormaltestResult(statistic=2.703801433319236, pvalue=0.2587479863488212)

根据输出可以看出，p 值为 0.26，大于 0.05，即接受 H0，原假设成立，人体体温服从正态分布

问题三：人体体温中存在的异常数据是哪些？

异常数据，这里采用两种检测方法

1.3σ 原则

3σ 原则又称为拉依达准则，该准则具体来说，就是先假设一组检测数据只含有随机误差，对原始数据进行计算处理得到标准差，然后按一定的概率确定一个区间，认为误差超过这个区间的就属于异常值。

正态分布状况下，数值分布表：

数值分布 在数据中的占比

(μ-σ,μ+σ) 0.6827

(μ-2σ,μ+2σ) 0.9545

(μ-3σ,μ+3σ) 0.9973

注：在正态分布中 σ 代表标准差, μ 代表均值，x=μ 为图形的对称轴

def three_sigma(Ser):
    '''
    Ser：表示传入DataFrame的某一列。
    '''
    low = Ser.mean()-3*Ser.std()
    up = Ser.mean()+3*Ser.std()
    drop_index = Ser.loc[(Ser < low) | (Ser > up)].index
    for i in drop_index:
        print(Ser[i])
    return drop_index, len(drop_index)

three_sigma(temp)

100.8

输出：

(Int64Index([129], dtype='int64'), 1)

根据输出，可以看出，使用 3σ 原则检测出来的人体体温中的异常数据只有一个，为 100.8

2.箱线图

箱型图提供了识别异常值的一个标准，即异常值通常被定义为小于 QL-1.5IQR 或大于 QU+1.5IQR 的值。

其中，QL 称为下四分位数，表示全部观察值中有四分之一的数据取值比它小；

QU 称为上四分位数，表示全部观察值中有四分之一的数据取值比它大；

IQR 称为四分位数间距，是上四分位数 QU 与下四分位数 QL 之差，其间包含了全部观察值的一半。

# 定义箱线图识别异常值函数
def box_plot(Ser):
    '''
    Ser：进行异常值分析的DataFrame的某一列
    '''
    low = Ser.quantile(0.25)-1.5*(Ser.quantile(0.75)-Ser.quantile(0.25))
    up = Ser.quantile(0.75)+1.5*(Ser.quantile(0.75)-Ser.quantile(0.25))
    drop_index = Ser.loc[(Ser < low) | (Ser > up)].index
    return drop_index, len(drop_index)

box_plot(temp)

输出

(Int64Index([0, 65, 129], dtype='int64'), 3)

def view_boxplot(Ser):
    plt.subplot(121)
    plt.boxplot(Ser)
    index, size = box_plot(Ser)
    for i in index:
        print(Ser[i])

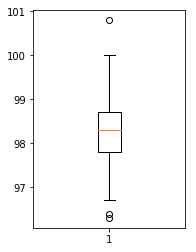
view_boxplot(temp)

96.3
96.4
100.8

根据输出可以看出，使用箱线图检测出来的人体体温中的异常数据有三个，分别为 96.3，96.4，100.8

问题四：男女体温是否存在明显差异？

这是两个正态总体均值差的假设检验问题

由于不确定男女的体温的方差是否相等，因此先用levene检验，检验两总体是否具有方差齐性，若得到的p值大于0.05，认为两总体具有方差齐性。

# levene检验两总体是否具有方差齐性
boy = data['Temperature'][data['Gender'] == 1]
girl = data['Temperature'][data['Gender'] == 2]
stats.levene(boy, girl)

输出：

LeveneResult(statistic=0.06354951292025163, pvalue=0.8013756068102883)

第二个输出为 p 值，可以看出，p 值为 0.80，远大于 0.05，可以认为两总体具有方差齐性。

接下来使用 stats.ttest_ind 函数来检验男女的体温是否存在明显的差异

stats.ttest_ind(boy, girl)

Ttest_indResult(statistic=-2.2854345381654984, pvalue=0.02393188312240236)

得到的 p 值小于 0.05，可以认为拒绝原假设，男女的体温存在明显的差异

问题五：体温与心率间的相关性(强？弱？中等?)

首先可以使用 seaborn 库中的 corr() 函数得到两个变量之间的相关系数，并画出散点图来直观表示

# 相关系数矩阵
temp.corr(heartRate)

0.2536564027207643

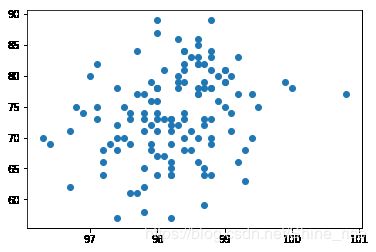
# 散点图
plt.scatter(temp, heartRate)

相关系数是 0.25， 并且根据图中也可以粗略判断其相关性是不强的

下面介绍两种判断相关系数的方法

1. pearson（皮尔逊）相关系数

要求样本满足正态分布

• 两个变量之间的皮尔逊相关系数定义为两个变量之间的协方差和标准差的商，其值介于-1与1之间

先判断两变量是否服从正态分布

stats.normaltest(temp, axis=0)

输出：

NormaltestResult(statistic=2.703801433319236, pvalue=0.2587479863488212)

stats.normaltest(heartRate, axis=0)

输出：

NormaltestResult(statistic=2.3488941072144778, pvalue=0.3089897872482146)

由于这两个变量的 p 值都大于 0.05，可以认为他们服从正态分布，接下来进行皮尔逊相关系数检验

stats.pearsonr(temp, heartRate)

输出：

(0.25365640272076423, 0.003591489250708233)

p值为 0.03，基本无相关性

2. Sperman 秩相关系数

皮尔森相关系数主要用于服从正太分布的连续变量

对于不服从正太分布的变量，分类关联性可采用 Sperman 秩相关系数，也称等级相关系数

由于本用例给出的变量服从正态分布，所以这里就不再进行 Sperman 秩相关系数检验了

欢迎关注微信公众号 shinerise，与你一起慢慢进步~