房间里面的财富分配游戏

1. 问题描述

2. 问题假设

3. 问题解决及可视化分析

• 初始化游戏
• 假设一 :不允许负债情况(财富值低于0即退出游戏)
• 假设二 :负债情况(投机者：即使财富为负依然消费)
• 假设三 :努力工作(奋斗者：负债情况下获得财富的几率多1%)
• 假设四 :存款利率(投资者：持有财富的年利率是3%
• 总结

1.问题描述

房间内有 100 人，每人有 100 块，每分钟随机 给另一个人 1 块钱，最后这个房间内的财富分布怎样？

2.问题假设

我们可以用这个游戏模拟现实社会上的财富运行及分配，有的人花钱，有的人挣钱，但是总资产不变。
假设：1.每个人在18岁带着100元的初始资金开始玩游戏；
2.每天玩一次，一直玩到80岁的人均寿命。
在现实社会中人的平均寿命为80岁，那么一生共需要玩大约20000次游戏，也就是说有20000次机会选择收钱或消费，只不过是随即分配的。
在此基础上，为进一步模拟现实社会，分为以下四种情况：
假设一 :不允许负债情况(财富值低于0即退出游戏)
假设二 :负债情况(投机者：即使财富为负依然消费)
假设三 :努力工作(奋斗者：负债情况下获得财富的几率多1%)
假设四 :存款利率(投资者：持有财富的年利率是3%）

3.问题解决

• 初始化游戏

#
#  初始化模拟世界
#
from random import choice, sample
import numpy as np

nLoops = 20000  # 分配的次数
nGamers = 100   # 参与分配的人数
deposit = 100   # 每个人初始财富数量
consume = 1        # 每次分配消费或者获得的财富

gamers = {}     # 用字典的方式保存每个人的财富数量并初始化
for gamer in range(nGamers):
    gamers[gamer] = deposit

计算每次随机分布的个人财富

# 计算每一次随机分配后的个人财富
def epoch(gamers, nGamers, consume, loan=False):
    """
    模拟每次分配的情况
       1 遍历全体参与者，获得参与者ID和拥有的财富
       2 随机挑选除自己以外的一个参与者
       3 自己消费财富同时挑选的参与者获得相应财富（注：考虑负债）
       
    参数：
        gamers - 分配游戏的参与者和其携带的财富数量；数据类型：字典，其中key为参与者ID，value为对应的财富数量
        nGamers - 参与分配游戏的总人数；数据类型：大于1的正整数
        consume - 参与每次分配消费或者获得的财富；数据类型：正整数
        loan - 当参与者携带的财富小于零的时候，是否允许参与本次分配的消费活动
    """

    for nid, nvalue in gamers.items():
        others = list(range(0,nGamers))
        del(others[nid])
        to_gamer = choice(others)
        if gamers[nid] <= 0 and not loan:
            continue
        gamers[to_gamer] += consume
        gamers[nid] -= consume
    
    return gamers

可视化结果：

def vis_simulation(nGamers, gamers, lucky_gamers=None):
    """
    模拟世界的财富分配 - 可视化结果
    
    参数：
        nGamers - 参与分配游戏的总人数；数据类型：大于1的正整数
        gamers - 分配游戏的参与者和其携带的财富数量；数据类型：字典，其中key为参与者ID，value为对应的财富数量
    """
    from matplotlib import pyplot as plt
    %matplotlib inline
    plt.rcParams['font.sans-serif'] = ['SimHei'] #指定默认字体
    plt.rcParams['axes.unicode_minus']=False #用来正常显示负号

    if lucky_gamers:
        new_gamers = []
        for i in lucky_gamers:
            new_gamers.append(gamers[i])

        sort_gamers = sorted(gamers.values())
        new_index = []
        for i in new_gamers:
            index = sort_gamers.index(i)
            new_index.append(index)
    
    
    # 可视化结果
    plt.figure(figsize=(18,6))
    plt.subplot(131)
    plt.hist(gamers.values())
    #plt.xlim([0,400])
    #plt.ylim([0,30])
    plt.title("财富的总体分布")

    plt.subplot(132)
    plt.bar(range(0,nGamers), gamers.values(), width=0.5, color='orange')
    if lucky_gamers:
        plt.bar(lucky_gamers, new_gamers, width=0.5, color='red')
    plt.plot([0,100],[100, 100],color='green',linestyle="-.",linewidth=1)
    plt.xlim([0,100])
    #plt.ylim([0,400])
    plt.title("个人持有财富的分布")
    
    plt.subplot(133)
    plt.bar(range(0,nGamers), sorted(gamers.values()), width=0.5, color='orange')
    if lucky_gamers:
        plt.bar(new_index, new_gamers, width=0.5, color='red')
    plt.plot([0,100],[100, 100],color='green',linestyle="-.",linewidth=1)
    plt.xlim([0,100])
    #plt.ylim([0,400])
    plt.title("排序后的个人持有财富分布")
    plt.show()

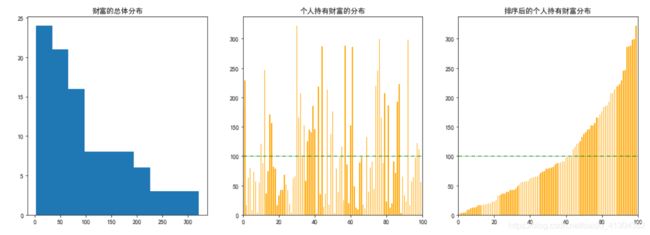
• 假设一
  不允许负债情况(财富值低于0即退出游戏)：

# 模拟分配 - 不负债的情况
for i in range(nLoops):
    gamers = epoch(gamers, nGamers, consume)
print(gamers)

输出：

可视化结果：

vis_simulation(nGamers, gamers)

• 假设二
  负债情况(投机者：即使财富为负依然消费)

gamers = {}     # 用字典的方式保存每个人的财富数量并初始化
for gamer in range(nGamers):
    gamers[gamer] = deposit

# 模拟分配 - 允许负债的情况
for i in range(nLoops):
    gamers = epoch(gamers, nGamers, consume, loan=True)
vis_simulation(nGamers, gamers)

• 假设三
  努力工作(奋斗者：负债情况下获得财富的几率多1%)

# 假如有某些比较努力的人们，计算每一次随机分配后的个人财富
def epoch_better_person(gamers, nGamers, consume, lucky_gamers, loan=False):
    """对于给定人数的游戏参与者， 每个人都随机的给其他人指定数量的货币（give）
       其中loan参数显示是否允许参与分配的人其财富为负值（即负债）
    """
    
    pass

gamers = {}     # 用字典的方式保存每个人的财富数量并初始化
for gamer in range(nGamers):
    gamers[gamer] = deposit

# 模拟分配 - 允许负债的情况 & 存在10个积极努力的参与者（奋斗者）
lucky_gamers = sample(range(0, nGamers), 10)
for i in range(nLoops):
    gamers = epoch_better_person(gamers, nGamers, consume, lucky_gamers, loan=True)
    
vis_simulation(nGamers, gamers, lucky_gamers=lucky_gamers)

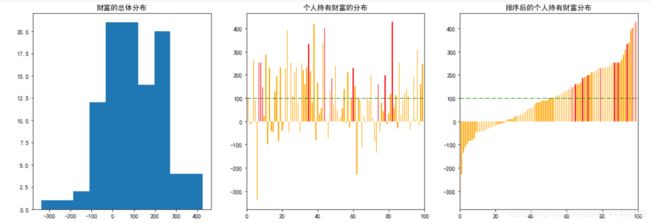
说明一下下：以上代码来自老师，我做了一下总结与修改，并增添了一个自己的…（嘿嘿）

• 假设四

import matplotlib.pyplot as plt#绘图库
import numpy as np#数据分析
import pandas as pd#数据分析
import random #随机函数
import time#计算时间
import copy#dataframe使用


plt.rcParams['font.sans-serif']=['SimHei']   # 用黑体显示中文
plt.rcParams['axes.unicode_minus']=False     # 正常显示负号

###定义方法：玩游戏#####
# 假设3(play_game3):存款利率(投资者：持有财富的年利率是3%)
def play_game3(round_number):   #round_number表示游戏的轮数
    id_list = range(100)  #定义每个人的编号
    id_money_dict = {k: 100 for k in id_list}  #定义初始每个人各#100元
    round_id_money_dict={}  #用于放每一轮游戏后每一个人的财富值，每一轮的数据都会保存
    for round_id in range(1,round_number+1):  #进行多轮游戏
        if round_id/365==0:
            for i in [0,11,22,33,44,55,66,77,88,99]:
                id_money_dict["i"]*=1.03 #每一年计算一次利率
        for id in id_money_dict.keys():   #每一轮中的每一个人都进行拿#钱和收钱的游戏
            id_money_dict[id] += -1     #其中一个人拿出一元钱
            id_get = random.randint(0, 99)   #随机选出另外一个
                                                    #收钱的人
            while id_get == id:
                id_get = random.randint(0, 99)  #如果出钱者
                                                    #钱者是同一个人，则重新选一个收钱者
                                                  
            id_money_dict[id_get] += 1   #另外一个人收下一元钱
        round_id_money_dict[round_id]=copy.copy(id_money_dict) #每一轮游戏过后，将数据存储在字典round_id_money_dict中                                              
    data_result=pd.DataFrame(round_id_money_dict)  #将每一轮游戏结束后的数据转化为DataFrame格式，便于取用和比较                         
                                   
    return(data_result) 
###定义方法：绘制柱状图#####
def draw1(data,n):   #data表示n轮后的数据，n表示游戏轮数   
    data=pd.DataFrame(data)
    data=data.T
    datai = pd.DataFrame({'money':data.iloc[0],'color':'gray'})
    datai['color'].loc[0,11,22,33,44,55,66,77,88,99] = 'red'
    datai = datai.sort_values(by = 'money').reset_index()
    plt.figure(figsize=(14,12))
    plt.bar(datai.index,datai['money'],color = datai['color'])
    plt.xticks(np.arange(100), datai["index"],fontsize=8,rotation=90)#设置坐标值
    plt.ylim([-300,500])
    plt.xlim([-10,110])
    plt.xlabel('玩家编号') #定义横坐标的名称
    plt.ylabel('财富值/元') #定义纵坐标的名称
    plt.title(str(n)+'轮游戏后的财富分布')
    
    plt.show()

'''
规定年利率为3%，那么一年后的财富为（1.03）*本金
规定id号为0,11,22,33,44,55,66,77,88,99的人为投资者
'''
 
#开始游戏
data_result=play_game3(20000)

##绘制十年，二十年，三十年，四十年，五十年后财富分布结果
for i in [3600,7200,10800,14400,18000]:
    start=time.time()
    draw1(data_result[i],i) 
    
    ##数据分析
    print("%d次游戏后数据分析："%i)
    
    #分析id号为0,11,22,33,44,55,66,76,88,99的人的财富情况
    print("投资者的财富值情况：")
    for j in [0,11,22,33,44,55,66,76,88,99]:
        print(data_result[i][j],end=" ") 
    
    ##投资者所拥有的财富占总财富的比例
    invest_money=0
    for x in [0,11,22,33,44,55,66,76,88,99]:
        invest_money+=data_result[i][x]
    print("投资者所拥有的财富占总财富的比例%s%%"%(invest_money/100))
    
    ## 分析第n次游戏，财富值排名前30的Id号
    rank_money = np.argsort(data_result[i])[90:100] # 返回排序后各数据的原始下标即从小到大排列财富值后，返回id号
    count=0#统计排名前三中那十个人的比例
    for m in rank_money:
        for n in [0,11,22,33,44,55,66,76,88,99]:
            if m==n:
                count+=1
    print("财富排行榜排名前十的人中,投资者共有%d个，所占比例为%s%%"%(count,count/3*10))
    
    end=time.time()#结束时间
    print("所用时间为："+str(end-start)+"s")
    

• 总结
  1.结合图表及数据可知，投资者的财富处于不确定的状态，在18-48岁时投资者的财富一直处于上升阶段，并且所有人的财富所占总体财富的比例也在上升，而48岁即10800次游戏后投资者所拥有的财富占总财富的比例开始下降，并且一旦负债之后就难以回归原来的初始值，而财富排行榜中,投资者所占比例也不是很多，告诉我们"投资有风险，需谨慎"

  2.尽管最成功的玩家不一定是最努力的那个，
  但是努力的人大都（80%）混的还不错。感谢这个残酷世界还给我们留下一条生路。
  那么，该如何面对这个残酷的世界？

那就是

努力 – 奋斗 并坚持下去