OpenGLES入门笔记：Rajawali学习（3.1）球体的绘制

背景

上一篇文章我们了解了Object3D类绘制3D模型的基本流程，现在我们使用一个实例来说明如何自定义一个基本的几何体模型。此处我们分析一下Rajawali中球体的实现，作为上一篇文章的补充说明。

实现

球型物体Sphere继承了Object3D。
下面我们看一下如何在Object3D的基础上扩展出来一个球型物体。

先看一下我们如何在场景中创建并添加一个Sphere

Sphere sphere = new Sphere(.3f, 12, 12);
        //下面一段均为父类提供的方法
        sphere.setMaterial(material);
        sphere.setColor(0x333333 + (int) (Math.random() * 0xcccccc));
        sphere.setX(-2);
        sphere.setY(0);
        sphere.setZ(1);
        sphere.setDrawingMode(GLES20.GL_TRIANGLES);

        mPicker.registerObject(sphere);
        getCurrentScene().addChild(sphere);

构造方法中提供了三个参数。第一个参数为球的半径，第二个第三个分别代表了球的宽高分别由多少个“段”组成。
下面我们看一下球体的构造函数

public Sphere(float radius, int segmentsW, int segmentsH, boolean createTextureCoordinates,
        boolean createVertexColorBuffer, boolean createVBOs, boolean mirrorTextureCoords) {
    super();
    mRadius = radius;
    mSegmentsW = segmentsW;
    mSegmentsH = segmentsH;
    //是否需要创建纹理
    mCreateTextureCoords = createTextureCoordinates;
    //是否需要添加颜色
    mCreateVertexColorBuffer = createVertexColorBuffer;
    //纹理是否需要镜像
    mMirrorTextureCoords = mirrorTextureCoords;
    //createVBOs 是否在setData时直接把顶点，法线等缓存中的信息赋值给GPU
    init(createVBOs);
}

这样，我们的目标就集中在init函数上了。这里，init函数做的事情其实就是根据我们设置的物体大小以及颜色来动态创建顶点，法线等数组，从而达到动态创建物体的效果。下面我们来分析一下这个init函数。首先看几个重要的变量。

//实际顶点个数
int numVertices = (mSegmentsW + 1) * (mSegmentsH + 1);
//实际图元三角形顶点个数
int numIndices = 2 * mSegmentsW * (mSegmentsH - 1) * 3;

//实际顶点坐标数组
float[] vertices = new float[numVertices * 3];
//实际法向量数组
float[] normals = new float[numVertices * 3];
//实际图元三角形索引数组
int[] indices = new int[numIndices];

indices就是我们得到的最后装配成三角形后的顶点数组。这个东西是怎么计算出来的呢？如下图所示
横着分为4段，竖着分为2段，即 mSegmentsW==4 mSegmentsH==2，根据上面的公式存储这8个三角形一共需要24个点，计算公式如上代码，我们可以参考一下下面这个示意图。水平方向有5个顶点，分成4段，也就是mSegmentsW为4，同理mSegmentsH为2，图中共有8个三角形，也就是需要存储24个顶点，所以索引数组大小为24.

生成球体的顶点

for (j = 0; j <= mSegmentsH; ++j) {
        float horAngle = (float) (Math.PI * j / mSegmentsH);
        float z = mRadius * (float) Math.cos(horAngle);
        float ringRadius = mRadius * (float) Math.sin(horAngle);

        //对于同一个z截面上
        for (i = 0; i <= mSegmentsW; ++i) {

            //x,y,z 使顶点坐标，同时这个向量也是顶点法向量
            float verAngle = (float) (2.0f * Math.PI * i / mSegmentsW);
            float x = ringRadius * (float) Math.cos(verAngle);
            float y = ringRadius * (float) Math.sin(verAngle);

            normals[vertIndex] = x * normLen;
            vertices[vertIndex++] = x;
            normals[vertIndex] = z * normLen;
            vertices[vertIndex++] = z;
            normals[vertIndex] = y * normLen;
            vertices[vertIndex++] = y;

            //求出每个三角形顶点在vertices缓冲中的索引
            if (i > 0 && j > 0) {
                int a = (mSegmentsW + 1) * j + i;
                int b = (mSegmentsW + 1) * j + i - 1;
                int c = (mSegmentsW + 1) * (j - 1) + i - 1;
                int d = (mSegmentsW + 1) * (j - 1) + i;

                if (j == mSegmentsH) {
                    indices[index++] = a;
                    indices[index++] = c;
                    indices[index++] = d;
                } else if (j == 1) {
                    indices[index++] = a;
                    indices[index++] = b;
                    indices[index++] = c;
                } else {
                    indices[index++] = a;
                    indices[index++] = b;
                    indices[index++] = c;
                    indices[index++] = a;
                    indices[index++] = c;
                    indices[index++] = d;
                }
            }
        }
    }

纹理相关

/**
*  设置纹理坐标数组
*/
float[] textureCoords = null;
    if (mCreateTextureCoords) {
        int numUvs = (mSegmentsH + 1) * (mSegmentsW + 1) * 2;
        textureCoords = new float[numUvs];

        numUvs = 0;
        for (j = 0; j <= mSegmentsH; ++j) {
            for (i = mSegmentsW; i >= 0; --i) {
                float u = (float) i / mSegmentsW;
                textureCoords[numUvs++] = mMirrorTextureCoords ? 1.0f - u : u;
                textureCoords[numUvs++] = (float) j / mSegmentsH;
            }
        }
    }

这里说一下textureCoords的UVs坐标。

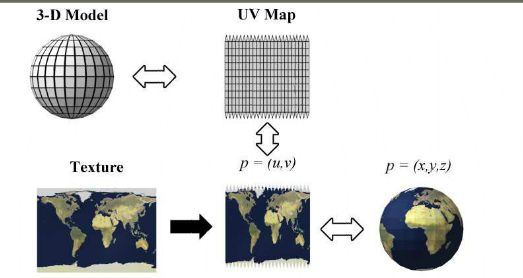
纹理坐标使用UVs，也就是在UV的一个二维平面上进行贴图，U为水平坐标，V是垂直坐标 UV点与模型上的点是一一对应的，可以看做是把一个二维图贴到一个三维平面上。此处注意 这里UV坐标都在0-1之间，这里计算的就是当前纹理长宽与总长宽的比值。如果不在0-1之间，纹理可能会出现重复的现象。下面一张图比较直观地说明了UVs与球体坐标的映射。

这样就完成了平面“裹”住球体的效果。注意，上面计算贴图数量的时候并不是用的三角形，二十直接用了我们设定的长宽。

赋值
这步相当于当前类已经撒手不干了，后面的东西都交给父类的方法进行处理。

setData(vertices, normals, textureCoords, colors, indices, createVBOs);

我们为父类传入顶点缓存，法线缓存，纹理，颜色和顶点索引缓存，之后的工作就交给Object3D中的方法进行绘制。

总结

球体的绘制为我们提供了绘制几何体的思路。首先我们要继承Object3D这个基类，我们通过调用基类的setData方法把顶点，法线等数据传给基类并进行绘制。所以，我们自己的定义的几何体类只需要提供顶点，法线，纹理，颜色，顶点索引这几个参数即可。我们可以在构造函数中进行这些参数的计算，并使用setData进行赋值，之后的事情全交给Object3D处理即可。