《数据结构与算法分析》寻找欧拉回路--多次修改最终复杂度O(E+V)
前言:
欧拉回路这一块,书上只用画图的方式解释了思路,然后说,采用合适的数据结构,可以把复杂度变为O(E+V),课本上简单的提及了一下,使用链表,并且保存指向最后扫描到的边的指针。当时无论怎么想都没有想明白,这到底要怎么样做才能实现。于是花了4,5个小时去网上搜寻博客,寻找oj相似的题目,寻找本书的答案。结果什么结果都没有得到。
最终决定,还是先实现基本的功能吧,不然这一章就白学了。然后从最基础的慢慢开始实现,实现的过程之中,自然就发现了如何将效率升高的方式了。接下来的博客我将仔细说明我是如何一步步修改过来的。
我的github:
我实现的代码全部贴在我的github中,欢迎大家去参观。
https://github.com/YinWenAtBIT
介绍:
欧拉回路:
一、定义:
欧拉回路:图G,若存在一条路,经过G中每条边有且仅有一次,称这条路为欧拉路,如果存在一条回路经过G每条边有且仅有一次,称这条回路为欧拉回路。具有欧拉回路的图成为欧拉图。
判断欧拉回路是否存在的方法
有向图:图连通,所有的顶点出度=入度。
无向图:图连通,所有顶点都是偶数度。
判断欧拉路是否存在的方法
有向图:图连通,有一个顶点出度大入度1,有一个顶点入度大出度1,其余都是出度=入度。
无向图:图连通,只有两个顶点是奇数度,其余都是偶数度的。
这里欧拉路不等同与欧拉回路。欧拉回路会在完成所有边的访问时回到出发的顶点。欧拉路会在完成所有边的访问之后结束于另一个顶点。算法步骤:
1.从起点开始,进行深度优先搜索,每访问一条边,就将该边删去,直到回到起点,并且没有相邻边可以访问。
2.从刚刚访问的路径上,寻找一个还有邻边的顶点,从该顶点开始,继续进行深度优先搜索,直到返回该顶点,新形成的环路添加进之前的环路。
3.重复过程2,直到所有的顶点的都不再有相邻的边。
为了实现这个算法,使用链表来存储顶点访问的顺序,添加新的环路只需要把开始的顶点替换成新得到的环路。
编码实现:
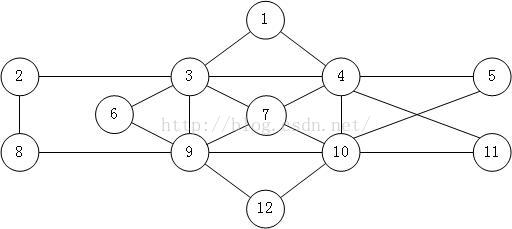
欧拉回路图:
在这里用来测试的欧拉回路图如上所示。起点定为5号点。
基础实现:
首先第一步就是实现最基础的深度优先搜索,在这里与前面的深度优先搜索不同的是,需要做到访问一条边之后,删除该边,知道最后回到起点,并且没有相邻的边为止。
基本功能编码:
void eulerDfs(Index S, List L, Graph G)
{
Index adj;
Edge edge = G->TheCells[S].next;
if(edge != NULL)
{
adj = edge->vertexIndex;
insert(adj, L);
removeEdgeWithIndexNoDirect(S, adj, G);
eulerDfs(adj, L->Next, G);
}
}5->10->11->4->10->5。
添加环:
有了第一步的环,现在可以考虑怎么样在链表中还有边的节点找出来,然后进行下一步的生成环了。
根据在别人博客上所看到的数据结构:
(1) 使用循环链表CList存储当前已经发现的环;
(2) 使用一个链表L保存当前环中还有出边的点;
(3) 使用邻接表存储图G读完它给的数据结构,我感觉还不够优化,于是我决定使用入度表来做这件事,在入度表所有顶点的入度变为0之前,还可以继续进行访问。寻找开始顶点的办法为:从保存路径的链表头开始搜索,找到直到第一个入度不为0的顶点,然后就从这个节点开始深度优先遍历。
编码如下:
List eulerCircuit(VertexType start, Graph G)
{
List Head = (List)malloc(sizeof(struct ListNode));
Head->Next = NULL;
Index P1;
P1 = FindKey(start, G);
if(G->TheCells[P1].Info != Legitimate)
return NULL;
Indegree inde = getIndegree(G);
insert(P1, Head);
eulerDfs(P1, Head->Next, G, inde);
while(!indeAllZero(inde, G->vertex))
{
List insertpoint = Head->Next;
Index Ptoin;
while(insertpoint!=NULL)
{
Ptoin = insertpoint->Element;
if(inde[Ptoin] != 0)
{
eulerDfs(Ptoin, insertpoint, G, inde);
break;
}
else
insertpoint = insertpoint->Next;
}
}
free(inde);
return Head;
}但是问题是这个复杂度估计很高,我进行了粗略的估计
复杂度如下:
1.获取入度表:O(E+V)
2.访问所有的边与定点O(E+V)
3.每完成一次回到出发点,需要查找一次入度表,共N次,O(N*V)。
4.根据已形成的环,寻找插入开始的起点,共N次,O(N*E)。
这样算下来,总的复杂度变成了O(N(E+V))。这样的结果与书上提出的O(E+V)差了十万八千里。于是接下来就该开始寻找可以优化的地方了。
根据课本中提到的:保留一个指向最后扫描到的边的指针。
现在看来变得更加的明确了,因为在进行深度优先搜索的过程中,需要对删去边的顶点进行入度减一操作,那么这个时候可以保存入度不为0的顶点,以及该顶点的位置,这样就可以不再需要循环寻找起始点了。
编码实现:
ListHead* eulerCircuit(VertexType start, Graph G)
{
Index P1;
P1 = FindKey(start, G);
if(G->TheCells[P1].Info != Legitimate)
return NULL;
ListHead* Head = (ListHead *)malloc(sizeof(struct ListHead));
Head->Next = NULL;
Head->Element =-1;
Head->insertPos = NULL;
Indegree inde = getIndegree(G);
insert(P1, Head);
eulerDfs(P1, Head->Next, G, inde, Head);
while(Head->Element != -1)
{
eulerDfs(Head->Element, Head->insertPos, G, inde, Head);
}
free(inde);
return Head;
}void eulerDfs(Index S, List L, Graph G, Indegree inde, ListHead* Head)
{
Index adj;
Edge edge = G->TheCells[S].next;
if(edge != NULL)
{
adj = edge->vertexIndex;
insert(adj, L);
removeEdgeWithIndexNoDirect(S, adj, G);
if(--inde[S] != 0)
{
Head->Element = S;
Head->insertPos = L;
}
else if(S == Head->Element)
Head->Element =-1;
/*避免只存在一个环的时候,访问结束于初始顶点,但它还被记录*/
if(--inde[adj] == 0 && adj == Head->Element)
Head->Element =-1;
eulerDfs(adj, L->Next, G, inde, Head);
}
}新的编码:
void eulerDfs(Index S, List L, Graph G, List inserPos)
{
Index adj;
Edge edge = G->TheCells[S].next;
if(edge != NULL)
{
adj = edge->vertexIndex;
insert(adj, L);
removeEdgeWithIndexNoDirect(S, adj, G);
if(G->TheCells[S].next != NULL)
{
inserPos->Element = S;
inserPos->Next = L;
}
else if(S == inserPos->Element)
inserPos->Element =-1;
/*避免只存在一个环的时候,访问结束于初始顶点,但它还被记录*/
if(G->TheCells[adj].next == NULL && adj == inserPos->Element)
inserPos->Element =-1;
eulerDfs(adj, L->Next, G, inserPos);
}
}
List eulerCircuit(VertexType start, Graph G)
{
Index P1;
P1 = FindKey(start, G);
if(G->TheCells[P1].Info != Legitimate)
return NULL;
List inserPos = (List)malloc(sizeof(struct ListNode));
inserPos->Next = NULL;
inserPos->Element =-1;
List Head = (List)malloc(sizeof(struct ListNode));
Head->Next = NULL;
insert(P1, Head);
eulerDfs(P1, Head->Next, G, inserPos);
while(inserPos->Element != -1)
{
eulerDfs(inserPos->Element, inserPos->Next, G, inserPos);
}
free(inserPos);
return Head;
}测试结果
先使用与上面给出的图进行测试,只列出节点号:
第一个的结果就是上图的输出结果,第二个结果是测试是否存在bug情况下给出的一个只有三个顶点,连成一个圈的图。
总结:
这一次的编码过程,让我明白了总是想找别人已经走过的路,再去做自己的实现,虽然快,但是很有可能是没有想要的结果的。这个时候应该果断的开始自行尝试,不要再浪费时间去寻找了。自己编码的过程中,说不定就明白了如何进行优化。总之,遇到不会的问题,先去尝试,至少先做出一个可以用的版本来再说。