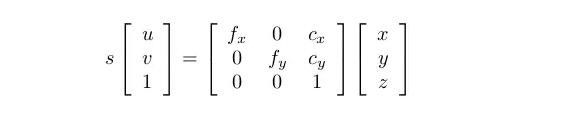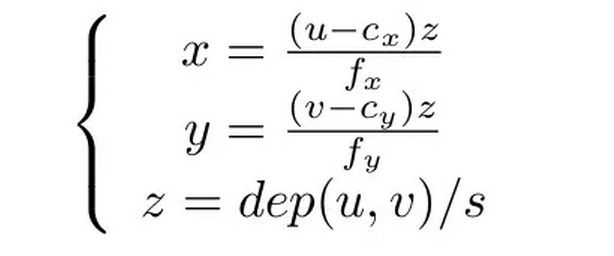SLAM导论
开始做SLAM(机器人同时定位与建图)研究已经近三年了。从博士一年级开始对这个方向产生兴趣,到现在为止,也算是对这个领域有了大致的了解。然而越了解,越觉得这个方向难度很大。总体来讲有以下几个原因:
1. 入门资料很少。虽然国内也有不少人在做,但这方面现在没有太好的入门教程。《SLAM for dummies》可以算是一篇。中文资料几乎没有。
2. SLAM研究已进行了三十多年,从上世纪的九十年代开始。其中又有若干历史分枝和争论,要把握它的走向就很费工夫。
3. 难以实现。SLAM是一个完整的系统,由许多个分支模块组成。现在经典的方案是“图像前端,优化后端,闭环检测”的三部曲,很多文献看完了自己实现不出来。
4. 自己动手编程需要学习大量的先决知识。首先你要会C和C++,网上很多代码还用了11标准的C++。第二要会用Linux。第三要会cmake,vim/emacs及一些编程工具。第四要会用openCV, PCL, Eigen等第三方库。只有学会了这些东西之后,你才能真正上手编一个SLAM系统。如果你要跑实际机器人,还要会ROS。
当然,困难多意味着收获也多,坎坷的道路才能锻炼人(比如说走着走着才发现Linux和C++才是我的真爱之类的。)鉴于目前网上关于视觉SLAM的资料极少,我于是想把自己这三年的经验与大家分享一下。说的不对的地方请大家批评指正。
这篇文章关注视觉SLAM,专指用摄像机,Kinect等深度像机来做导航和探索,且主要关心室内部分。到目前为止,视觉SLAM的框架已基本成熟,可以在运动稳定、光照充足的环境中,在厘米级别的误差范围内进行定位与建图。但是,离充满动态光照和人群密集的现实环境,要应用视觉SLAM技术,仍有很长的路要走。以下,我会介绍SLAM的历史、理论以及实现的方式,且主要介绍视觉(Kinect)的实现方式。
| SLAM问题
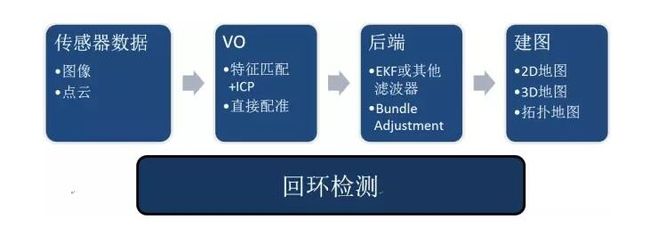
SLAM,全称叫做Simultaneous Localization and Mapping,中文叫做同时定位与建图。大体说来,一个SLAM系统分为四个模块(除去传感器数据读取),如下图所示:
啊不行,这么讲下去,这篇文章肯定没有人读,所以我们换一个讲法,引入机器人“小萝卜”同学。
小萝卜的故事
从前,有一个机器人叫“小萝卜”。它长着一双乌黑发亮的大眼睛,叫做Kinect。有一天,它被邪恶的科学家关进了一间空屋子,里面放满了杂七杂八的东西。
小萝卜感到很害怕,因为这个地方他从来没来过,一点儿也不了解。让他感到害怕的主要是三个问题:
1. 自己在哪里?
2. 这是什么地方?
3. 怎么离开这个地方?
在SLAM理论中,第一个问题称为定位 (Localization),第二个称为建图 (Mapping),第三个则是随后的路径规划。我们希望借助Kinect工具,帮小萝卜解决这个难题。各位同学有什么思路呢?
| Kinect数据
要打败敌人,首先要了解你的武器。不错,我们先介绍一下Kinect。众所周知这是一款深度相机,你或许还听说过别的牌子,但Kinect的价格便宜,测量范围在3m-12m之间,精度约3cm,较适合于小萝卜这样的室内机器人。它采到的图像是这个样子的(从左往右依次为rgb图,深度图与点云图):
Kinect的一大优势在于能比较廉价地获得每个像素的深度值,不管是从时间上还是从经济上来说。OK,有了这些信息,小萝卜事实上可以知道它采集到的图片中,每一个点的3d位置。只要我们事先标定了Kinect,或者采用出厂的标定值。
我们把坐标系设成这个样子,这也是openCV中采用的默认坐标系。
o’-uv是图片坐标系,o-xyz是Kinect的坐标系。假设图片中的点为(u,v),对应的三维点位置在(x,y,z),那么它们之间的转换关系是这样的:
或者更简单的:
后一个公式给出了计算三维点的方法。先从深度图中读取深度数据(Kinect给的是16位无符号整数),除掉z方向的缩放因子,这样你就把一个整数变到了以米为单位的数据。然后,x,y用上面的公式算出。一点都不难,就是一个中心点位置和一个焦距而已。f代表焦距,c代表中心。如果你没有自己标定你的Kinect,也可以采用默认的值:s=5000, cx = 320, cy=240, fx=fy=525。实际值会有一点偏差,但不会太大。
| 定位问题
知道了Kinect中每个点的位置后,接下来我们要做的,就是根据两帧图像间的差别计算小萝卜的位移。比如下面两张图,后一张是在前一张之后1秒采集到的:
你肯定可以看出,小萝卜往右转过了一定的角度。但究竟转过多少度呢?这就要靠计算机来求解了。这个问题称为相机相对姿态估计,经典的算法是ICP(Iterative Closest Point,迭代最近点)。
这个算法要求知道这两个图像间的一组匹配点,说的通俗点,就是左边图像哪些点和右边是一样的。你当然看见那块黑白相间的板子同时出现在两张图像中。
在小萝卜看来,这里牵涉到两个简单的问题:特征点的提取和匹配。
如果你熟悉计算机视觉,那你应该听说过SIFT, SURF之类的特征。不错,要解决定位问题,首先要得到两张图像的一个匹配。匹配的基础是图像的特征,下图就是SIFT提取的关键点与匹配结果:
对实现代码感兴趣的同学请Google“opencv 匹配”即可,在openCV的教程上也有很明白的例子。上面的例子可以看出,我们找到了一些匹配,但其中有些是对的(基本平等的匹配线),有些是错的。这是由于图像中存在周期性出现的纹理(黑白块),所以容易搞错。但这并不是问题,在接下来的处理中我们会将这些影响消去。
得到了一组匹配点后,我们就可以计算两个图像间的转换关系,也叫PnP问题。它的模型是这样的:
R为相机的姿态,C为相机的标定矩阵。R是不断运动的,而C则是随着相机做死的。ICP的模型稍有不同,但原理上也是计算相机的姿态矩阵。原则上,只要有四组匹配点,就可以算这个矩阵。你可以调用openCV的SolvePnPRANSAC函数或者PCL的ICP算法来求解。openCV提供的算法是RANSAC(Random Sample Consensus,随机采样一致性)架构,可以剔除错误匹配。所以代码实际运行时,可以很好地找到匹配点。以下是一个结果的示例。
上面两张图转过了16.63度,位移几乎没有。
有同学会说,那只要不断匹配下去,定位问题不就解决了吗?表面上看来,的确是这样的,只要我们引入一个关键帧的结构(发现位移超过一个固定值时,定义成一个关键帧)。然后,把新的图像与关键帧比较就行了。至于建图,就是把这些关键帧的点云拼起来,看着还有模有样,煞有介事的:
然而,如果事情真这么简单,SLAM理论就不用那么多人研究三十多年了(它是从上世纪90年代开始研究的)(上面讲的那些东西简直随便哪里找个小硕士就能做出来……)。那么,问题难在什么地方呢?
| SLAM端优化理论
最麻烦的问题,就是“噪声”。这种渐近式的匹配方式,和那些惯性测量设备一样,存在着累积噪声。因为我们在不断地更新关键帧,把新图像与最近的关键帧比较,从而获得机器人的位移信息。但是你要想到,如果有一个关键帧出现了偏移,那么剩下的位移估计都会多出一个误差。这个误差还会累积,因为后面的估计都基于前面的机器人位置……
哇!这后果简直不堪设想啊。例如,你的机器人往右转了30度,再往左转了30度回到原来的位置。然而由于误差,你算成了向右转29度,再向左转31度,这样你构建的地图中,会出现初始位置的两个“重影”。
我们能不能想办法消除这个该死的误差呢?
朋友们,这才是SLAM的研究,前面的可以说是“图像前端”的处理方法。我们的解决思路是:
如果你和最近的关键帧相比,会导致累计误差。那么,我们最好是和更前面的关键帧相比,而且多比较几个帧,不要只比较一次。
我们用数学来描述这个问题。设:
不要怕,只有借助数学才能把这个问题讲清楚。上面的公式中,xp是机器人小萝卜的位置,我们假定由n个帧组成。xL则是路标,在我们的图像处理过程中就是指SIFT提出来的关键点。如果你做2D SLAM,那么机器人位置就是x, y加一个转角theta。如果是3D SLAM,就是x,y,z加一个四元数姿态(或者rpy姿态)。这个过程叫做参数化(Parameterization)。
不管你用哪种参数,后面两个方程你都需要知道。前一个叫运动方程,描述机器人怎样运动。u是机器人的输入,w是噪声。这个方程最简单的形式,就是你能通过什么方式(码盘等)获得两帧间的位移差,那么这个方程就直接是上一帧与u相加即得。另外,你也可以完全不用惯性测量设备,这样我们就只依靠图像设备来估计,这也是可以的。
后一个方程叫观测方程,描述那些路标是怎么来的。你在第i帧看到了第j个路标,产生了一个测量值,就是图像中的横纵坐标。最后一项是噪声。偷偷告诉你,这个方程形式上和上一页的那个方程是一模一样的。
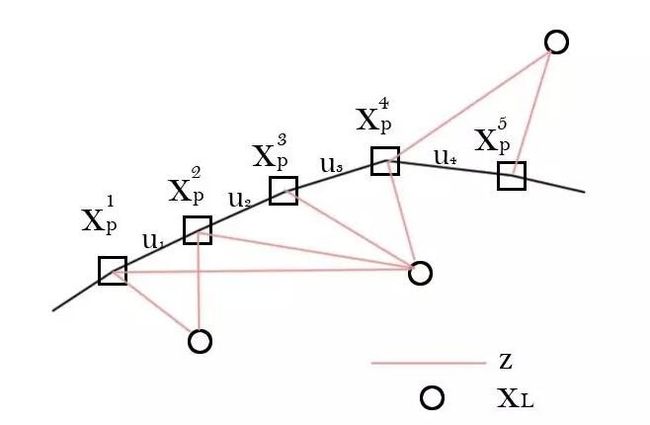
在求解SLAM问题前,我们要看到,我们拥有的数据是什么?在上面的模型里,我们知道的是运动信息u以及观测z。用示意图表示出来是这样的:
我们要求解的,就是根据这些u和z,确定所有的xp和xL。这就是SLAM问题的理论。
从SLAM诞生开始科学家们就一直在解决这个问题。最初,我们用Kalman滤波器,所以上面的模型(运动方程和观测方程)被建成这个样子。直到21世纪初,卡尔曼滤波器仍在SLAM系统占据最主要的地位,Davison经典的单目SLAM就是用EKF做的。但是后来,出现了基于图优化的SLAM方法,渐渐有取而代之的地位[1]。我们在这里不介绍卡尔曼滤波器,有兴趣的同学可以在wiki上找卡尔曼滤波器,另有一篇中文的《卡尔曼滤波器介绍》也很棒。由于滤波器方法存储n个路标要消耗n平方的空间,在计算量上有点对不住大家。尽管08年有人提出分治法的滤波器能把复杂度弄到O(n) [2],但实现手段比较复杂。我们要介绍那种新兴的方法: Graph-based SLAM。
图优化方法把SLAM问题做成了一个优化问题。学过运筹学的同学应该明白,优化问题对我们有多么重要。我们不是要求解机器人的位置和路标位置吗?我们可以先做一个猜测,猜想它们大概在什么地方。这其实是不难的。然后呢,将猜测值与运动模型/观测模型给出的值相比较,可以算出误差:
通俗一点地讲,例如,我猜机器人第一帧在(0,0,0),第二帧在(0,0,1)。但是u1告诉我机器人往z方向(前方)走了0.9米,那么运动方程就出现了0.1m的误差。同时,第一帧中机器人发现了路标1,它在该机器人图像的正中间;第二帧却发现它在中间偏右的位置。这时我们猜测机器人只是往前走,也是存在误差的。至于这个误差是多少,可以根据观测方程算出来。
我们得到了一堆误差,把这些误差平方后加起来(因为单纯的误差有正有负,然而平方误差可以改成其他的范数,只是平方更常用),就得到了平方误差和。我们把这个和记作phi,就是我们优化问题的目标函数。而优化变量就是那些个xp, xL。
改变优化变量,误差平方和(目标函数)就会相应地变大或变小,我们可以用数值方法求它们的梯度和二阶梯度矩阵,然后用梯度下降法求最优值。这些东西学过优化的同学都懂的。
注意到,一次机器人SLAM过程中,往往会有成千上万帧。而每一帧我们都有几百个关键点,一乘就是几百万个优化变量。这个规模的优化问题放到小萝卜的机载小破本上可解吗?是的,过去的同学都以为,Graph-based SLAM是无法计算的。但就在21世纪06,07年后,有些同学发现了,这个问题规模没有想象的那么大。上面的J和H两个矩阵是“稀疏矩阵”,于是呢,我们可以用稀疏代数的方法来解这个问题。“稀疏”的原因,在于每一个路标,往往不可能出现在所有运动过程中,通常只出现在一小部分图像里。正是这个稀疏性,使得优化思路成为了现实。
优化方法利用了所有可以用到的信息(称为full-SLAM, global SLAM),其精确度要比我们一开始讲的帧间匹配高很多。当然计算量也要高一些。
由于优化的稀疏性,人们喜欢用“图”来表达这个问题。所谓图,就是由节点和边组成的东西。我写成G={V,E},大家就明白了。V是优化变量节点,E表示运动/观测方程的约束。什么,更糊涂了吗?那我就上一张图,来自[3]。
图有点模糊,而且数学符号和我用的不太一样,我用它来给大家一个图优化的直观形象。
上图中,p是机器人位置,l是路标,z是观测,t是位移。其中呢,p, l是优化变量,而z,t是优化的约束。看起来是不是像一些弹簧连接了一些质点呢?因为每个路标不可能出现在每一帧中,所以这个图是蛮稀疏的。
不过,“图”优化只是优化问题的一个表达形式,并不影响优化的含义。实际解起来时还是要用数值法找梯度的。这种思路在计算机视觉里,也叫做Bundle Adjustment。它的具体方法请参见一篇经典文章[4]。
不过,BA的实现方法太复杂,不太建议同学们拿C来写。好在2010年的ICRA上,其他的同学们提供了一个通用的开发包:g2o [5]。它是有图优化通用求解器,很好用,我改天再详细介绍这个软件包。总之,我们只要把观测和运动信息丢到求解器里就行。这个优化器会为我们求出机器人的轨迹和路标位置。如下图,红点是路标,蓝色箭头是机器人的位置和转角(2D SLAM)。细心的同学会发现它往右偏转了一些:
| 闭环检测
上面提到,仅用帧间匹配最大的问题在于误差累积,图优化的方法可以有效地减少累计误差。然而,如果把所有测量都丢进g2o,计算量还是有点儿大的。根据我自己测试,约10000多条边,g2o跑起来就有些吃力了。这样,就有同学说,能把这个图构造地简洁一些吗?我们用不着所有的信息,只需要把有用的拿出来就行了。
事实上,小萝卜在探索房间时,经常会左转一下,右转一下。如果在某个时刻他回到了以前去过的地方,我们就直接与那时候采集的关键帧做比较,可以吗?我们说,可以,而且那是最好的方法。这个问题叫做闭环检测。
闭环检测是说,新来一张图像时,如何判断它以前是否在图像序列中出现过?
有两种思路:一是根据我们估计的机器人位置,看是否与以前某个位置邻近;二是根据图像的外观,看它是否和以前关键帧相似。
目前主流方法是后一种,因为很多科学家认为前一种依靠有噪声的位置来减少位置的噪声,有点循环论证的意思。后一种方法呢,本质上是个模式识别问题(非监督聚类,分类),常用的是Bag-of-Words (BOW)。但是BOW需要事先对字典进行训练,因此SLAM研究者仍在探讨有没有更合适的方法
在Kinect SLAM经典大作中[6],作者采用了比较简单的闭环方法:在前面n个关键帧中随机采k个,与当前帧两两匹配。匹配上后认为出现闭环。这个真是相当的简单实用,效率也过得去。
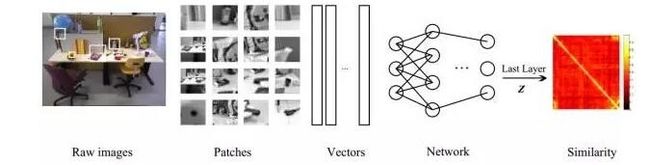
高效的闭环检测是SLAM精确求解的基础。研究者也在尝试利用深度学习技术提高闭环检测的精度,例如本文作者发表在Autonomous Robot期刊上的论文Unsupervised Learning to Detect Loops Using Deep Neural Networks for Visual SLAM System采用了无监督的深度自动编码机从原始输入图像中学习紧凑的图像表示,相比于传统的Bag of Word方法提高了闭环检测的鲁棒性。方法流程图如下[7]:
| 小结
本文我们介绍了SLAM的基本概念,重点介绍了图优化解决SLAM问题的思路。本文作者编写了一个基于RGB-D相机的SLAM程序(点击可进入github地址),它是一个Linux下基于cmake的工程。
参考文献
[1] Visual SLAM: Why filter? Strasdat et. al., Image and Vision Computing, 2012.
[2] Divide and Conquer: EKF SLAM in O(n), Paz Lina M et al., IEEE Transaction on Robotics, 2008
[3] Relative bundle adjustment, Sibley, Gabe, 2009
[4] Bundle adjustment - a Modern Synthesis. Triggs B et. el., Springer, 2000
[5] g2o: A General Framework for Graph Optimization, Kummerle Rainer, et. al., ICRA, 2011
[6] 3-D Mapping with an RGB-D Camera, IEEE Transaction on Robotics, Endres et al., 2014
[7] Xiang Gao, Tao Zhang, Unsupervised Learning to Detect Loops Using Deep Neural Networks for Visual SLAM System, Autonomous Robot, 2015.