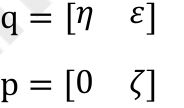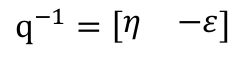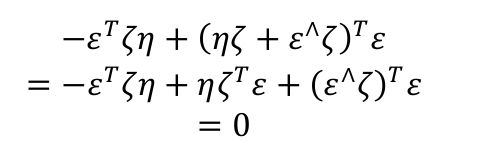SLAM学习小组 : 视觉SLAM十四讲 第三讲 + 视觉SLAM理论与实践 第二节
一、熟悉Eigen矩阵运算
Wiki Eigen
设线性⽅程 Ax = b，在 A 为⽅阵的前提下，请回答以下问题：
1. 在什么条件下，x 有解且唯⼀？
线性方程组的矩阵满秩（非奇异矩阵）
2. 高斯消元法的原理是什么？
高斯消元法是将方程组中的一方程的未知数用含有另一未知数的代数式表示，并将其代人到另一方程中，这就消去了一未知数，得到一解；或将方程组中的一方程倍乘某个常数加到另外一方程中去，也可达到消去一未知数的目的。消元法主要用于二元一次方程组的求解。
在用系数矩阵表示的线性方程组中，高斯消元的过程就是将原来系数矩阵化为上三角矩阵的过程。主要是用初等变换将某一行倍乘后加到另一行，从而在下三角部分引入零元，变换以后所得线性代数方程组系数矩阵为上三角，很容易用回代求解。
4. QR 分解的原理是什么？
如果实（复）非奇异矩阵A能够化成正交（酉）矩阵Q与实（复）上三角矩阵R的乘积，即A=QR，则称其为A的QR分解。（列满秩矩阵必有QR分解）（当要求R的对角线元素为正时，该分解唯一）
其中Q的列向量是A的列空间的标准正交基，R是一个非奇异可逆的上三角矩阵
5. Cholesky 分解的原理是什么？
Cholesky 分解是把一个对称正定的矩阵表示成一个下三角矩阵L和其转置的乘积的分解。它要求矩阵的所有特征值必须大于零，故分解的下三角的对角元也是大于零的。Cholesky分解法又称平方根法，是当A为实对称正定矩阵时，LU三角分解法的变形。
6. 编程实现 A 为 100 × 100 随机矩阵时，⽤ QR 和 Cholesky 分解求 x 的程序。你可以参考本次课用到的 useEigen 例程。
运行环境QT creator
#include <iostream>
using namespace std;
#include <ctime>
// Eigen 部分
#include <eigen3/Eigen/Core>
// 稠密矩阵的代数运算（逆，特征值等）
#include <eigen3/Eigen/Dense>
#define MATRIX_SIZE 100
/****************************
* 本程序演示了 Eigen 基本类型的使用
****************************/
int main( int argc, char** argv )
{
// 解方程
// 我们求解 matrix_NN * x = v_Nd 这个方程
// N的大小在前边的宏里定义，它由随机数生成
// 直接求逆自然是最直接的，但是求逆运算量大
Eigen::Matrix< double, Eigen::Dynamic, Eigen::Dynamic > x;
Eigen::Matrix< double, Eigen::Dynamic, Eigen::Dynamic > x2;
Eigen::Matrix< double, MATRIX_SIZE, MATRIX_SIZE > matrix_NN;
matrix_NN = Eigen::MatrixXd::Random( MATRIX_SIZE, MATRIX_SIZE );
Eigen::Matrix< double, MATRIX_SIZE, 1> v_Nd;
v_Nd = Eigen::MatrixXd::Random( MATRIX_SIZE,1 );
clock_t time_stt = clock(); // 计时
// 通常用矩阵分解来求，例如QR分解，速度会快很多
time_stt = clock();
x = matrix_NN.colPivHouseholderQr().solve(v_Nd);
cout <<"time use in Qr decomposition is " <<1000* (clock() - time_stt)/(double)CLOCKS_PER_SEC <<"ms" << endl;
cout << x << endl;
// x2 = matrix_NN.llt().solve(v_Nd);
//cout <<"time use in Cholesky decomposition is " <<1000* (clock() - time_stt)/(double)CLOCKS_PER_SEC <<"ms" << endl;
//cout << x2 << endl;
return 0;
}
QR：
Cholesky:
提⽰：你可能需要参考相关的数学书籍或⽂章。请善⽤搜索引擎。Eigen 固定⼤⼩矩阵最⼤⽀持到 50，
所以你会⽤到动态⼤⼩的矩阵。
二、几何运算练习
运行环境QT creator
#include <iostream>
#include <cmath>
using namespace std;
#include <eigen3/Eigen/Core>
// Eigen 几何模块
#include <eigen3/Eigen/Geometry>
/****************************
* 本程序演示了 Eigen 几何模块的使用方法
****************************/
int main ( int argc, char** argv )
{
Eigen::Quaterniond q1(0.55,0.3,0.2,0.2);
Eigen::Quaterniond q2(-0.1,0.3,-0.7,0.2);
q1= q1.normalized();
q2= q2.normalized();
Eigen::Matrix3d R_ = q1.matrix().inverse();
Eigen::Matrix3d R2 = q2.matrix();
Eigen::Matrix<double,3,1> P1;
Eigen::Matrix<double,3,1> P2;
Eigen::Matrix<double,3,1> t1;
Eigen::Matrix<double,3,1> t2;
P1 << 0.5,-0.1,0.2;
t1 << 0.7,1.1,0.2;
t2 << -0.1,0.4,0.8;
P2 = R2 * R_ * (P1-t1) + t2;
cout<<"quaternion = \n"<<P2 <<endl; // 请注意coeffs的顺序是(x,y,z,w),w为实部，前三者为虚部
// cout<<"quaternion = \n"<
// cout<<"quaternion = \n"<
// cout<<"quaternion = \n"<
return 0;
}
三、 旋转的表达
证明：
- 设有旋转矩阵 R,证明 R T R = I 且 det R = +1
旋转矩阵是由三个正交的单位向量定义的所以它是正交矩阵，因为是正交矩阵所以它的转置等于它的逆，所以RTR=I
正交变换的矩阵的行列式等于1或-1,规定行列式等于1正交变换称为旋转变换,行列式等于-1正交变换称为镜面反射，所以“旋转变换的矩阵的行列式为+1” - 设有四元数 q,我们把虚部记为 ε,实部记为 η,那么 q = (ε, η)。请说明 ε 和 η 的维度。
ε虚部：三维
η实部：一维 - 定义运算
+和⊕为:
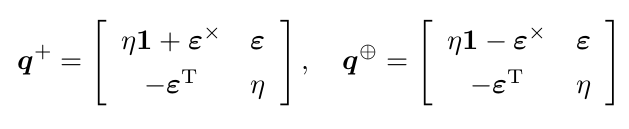
其中x含义与^相同，即取ε的反对称矩阵(它们都成叉积的矩阵运算形式)，1为单位矩阵。请证明对任意单位四元数 q 1 , q 2 ,四元数乘法可写成矩阵乘法:
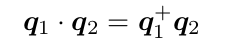
或
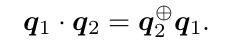
证：
四、 罗德里格斯公式的证明
罗德里格斯公式描述了从旋转向量到旋转矩阵的转换关系。设旋转向量长度为 θ,方向为 n,那么旋转矩阵 R 为:
参考https://en.wikipedia.org/wiki/Rodrigues%27_rotation_formula
证：
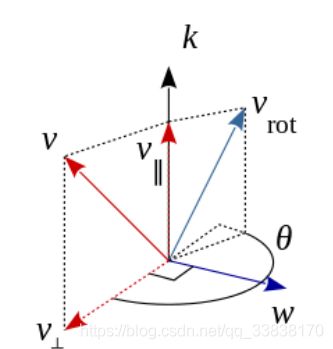旋转前根据矩阵投影公式可得：
则旋转后矢量为：
则旋转矩阵为：
五、四元数运算性质的验证
证明p ′ = qpq (−1) 是虚四元数;此外,上式亦可写成矩阵运算:p ′ = Qp。请根据你的推导,给出矩阵 Q。注意此时 p 和 p ′ 都是四元数形式的变量,所以 Q 为 4 × 4 的矩阵。
设：
有：
又有：
qpq (−1)的实部为：
qpq (−1)的虚部为：
R为：
六、 熟悉C++11
for：区间迭代
auto&：自动推导类型
[](const A&a1,const A&a2) {return a1.index