凑硬币问题

题目描述

给出任意一堆硬币，然后我们需要凑到k元钱，问一共有多少种凑法。

• 输入格式
  t
  length target
  coin1 coin2 coin3…
• 输出格式
  count

举个例子，现在有1元、2元、5元硬币，要凑成5元，一共有多少种方式？
输入：1 3 5 1 2 5
输出：4
我们一看就能知道结果：
1+1+1+1+1
1+1+1+2
1+2+2
5
一共是4种。

解决方式1：回溯法

这里其实有点类似leetcode上的一个系列的题——combination sum，我们可以用回溯法来解决。

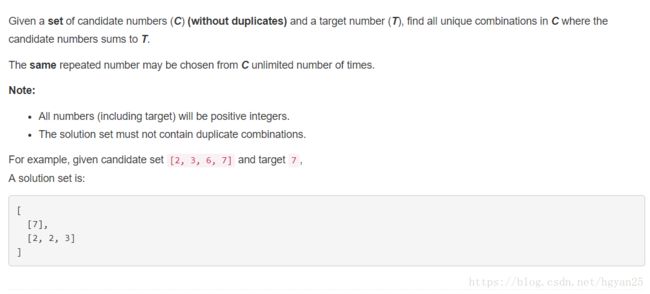
- 首先对硬币进行排序
- 然后开始查找是否有满足的组合数
用递归来实现，我们设置target为组合数之和，result记录所有组合数的list，combination记录组合数
- 每次加入一个candidate值(其实就是钱币数)时，我们要判断当前的target>=candidate[i],不然加了一个比target还大的candidate就没意义了嘛。
- 每次加了一个coin值后，target值= target - coin[i]
- 然后如果target==0，也就是所当前的这个组合数已经满足了我们需要的条件，我们可以将它放入result中
- 如果target>0，我们还要继续加，从index开始，这里的index记录的是上一次用到的那个index，因为可以重复加嘛。
当完成查找的操作之后，进行回溯，其实就是将加进去combination的值再取出来嘛。
- 最后，我们得到的result就是最终的结果了。
这里求的是数量，我们可以求result的长度。但是呢要考虑到内存的问题。其实做一个小小的变换，我们不需要存储组合数，传入一个count值，每次得到target==0时，count+1即可。
最终count值即为所求。

解决方式2：动态规划

当然啦，上面的方法超时了，不得不改用其他算法来实现。
这里实现了一个动态规划的问题。用的是一个二维数组的方式。
我们来分析下，现在有三种类型的硬币
我们建立一个二维数组dp[4][target+1]，那么第一维表示用的第几个硬币，第二维表示凑成k元。
那么dp[i][target]表示用第i个硬币凑成target元的凑法。
第i个硬币的价值为coin[i-1]

dp[i][target]=dp[i−1][target−0∗coin[i−1]]+dp[i−1][target−1∗coin[i−1]]+...+dp[i−1][target−(target/coin[i−1])∗coin[i−1]] d p [ i ] [ t a r g e t ] = d p [ i − 1 ] [ t a r g e t − 0 ∗ c o i n [ i − 1 ] ] + d p [ i − 1 ] [ t a r g e t − 1 ∗ c o i n [ i − 1 ] ] + . . . + d p [ i − 1 ] [ t a r g e t − ( t a r g e t / c o i n [ i − 1 ] ) ∗ c o i n [ i − 1 ] ]

简单理解：假设现在 i=3 i = 3 ,即coin值为5，那么要算用两个硬币凑成5元以及两个硬币凑成0元的数量，得到的结果即为所求。

dp[3][5]=dp[2][5]+dp[2][0] d p [ 3 ] [ 5 ] = d p [ 2 ] [ 5 ] + d p [ 2 ] [ 0 ]

直接粗暴的来看代码

long countWays_2(int target, int length, int *coins) {
    long dp[length+2][target+1] = {0};  
    for (int i = 1; i <=target; i++) {
        dp[0][i] = 0;//用0种硬币凑成i元的组合数为0
    }
    for (int i = 0; i <= length; i++) {
        dp[i][0] = 1;//用i种硬币凑成0元的组合数为1
    }
    for (int i = 1; i <= length; i++) {
        for (int j = 1; j <= target; j++) {
            dp[i][j]= 0;
            for (int k = 0; k <=j/coins[i-1]; k++) {
                dp[i][j] += dp[i-1][j-k*coins[i-1]];
            }
        }
    }
    return dp[length][target];
}

这样子做不仅速度加快了，消耗的内存也减少了。

更多

当然啦，如果有更好的解法，欢迎分享探讨