一、背景
1.项目描述
- 你拥有一个超市(Supermarket Mall)。通过会员卡,你用有一些关于你的客户的基本数据,如客户ID,年龄,性别,年收入和消费分数。
- 消费分数是根据客户行为和购买数据等定义的参数分配给客户的。
- 问题陈述:你拥有这个商场。想要了解怎么样的顾客可以很容易地聚集在一起(目标顾客),以便可以给营销团队以灵感并相应地计划策略。
2.数据描述
| 字段名 | 描述 |
|---|---|
| CustomerID | 客户编号 |
| Gender | 性别 |
| Age | 年龄 |
| Annual Income (k$) | 年收入,单位为千美元 |
| Spending Score (1-100) | 消费分数,范围在1~100 |
二、相关模块
import numpy as np import pandas as pd
from pandas import plotting import matplotlib.pyplot as plt import seaborn as sns import plotly.graph_objs as go import plotly.offline as py
from sklearn.cluster import KMeans
import warnings
warnings.filterwarnings('ignore')
三、数据可视化
1.数据读取
io = '.../Mall_Customers.csv'
df = pd.DataFrame(pd.read_csv(io))
# 修改列名
df.rename(columns={'Annual Income (k$)': 'Annual Income', 'Spending Score (1-100)': 'Spending Score'}, inplace=True)
print(df.head())
print(df.describe())
print(df.shape)
print(df.count())
print(df.dtypes)
输出如下。
CustomerID Gender Age Annual Income Spending Score
0 1 Male 19 15 39
1 2 Male 21 15 81
2 3 Female 20 16 6
3 4 Female 23 16 77
4 5 Female 31 17 40
-----------------------------------------------------------------
CustomerID Age Annual Income Spending Score
count 200.000000 200.000000 200.000000 200.000000
mean 100.500000 38.850000 60.560000 50.200000
std 57.879185 13.969007 26.264721 25.823522
min 1.000000 18.000000 15.000000 1.000000
25% 50.750000 28.750000 41.500000 34.750000
50% 100.500000 36.000000 61.500000 50.000000
75% 150.250000 49.000000 78.000000 73.000000
max 200.000000 70.000000 137.000000 99.000000
-----------------------------------------------------------------
(200, 5)
CustomerID 200
Gender 200
Age 200
Annual Income 200
Spending Score 200
dtype: int64
-----------------------------------------------------------------
CustomerID int64
Gender object
Age int64
Annual Income int64
Spending Score int64
dtype: object
2.数据可视化
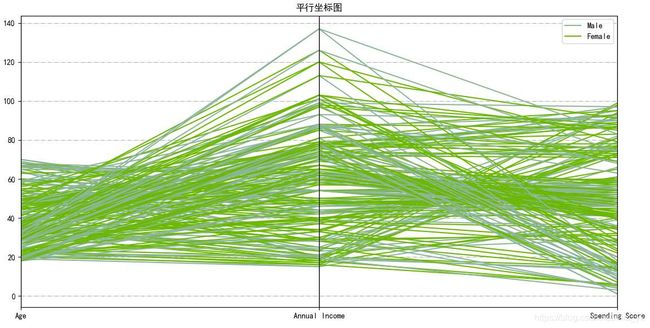
2.1 平行坐标图
- 平行坐标图(Parallel coordinates plot)用于多元数据的可视化,将高维数据的各个属性(变量)用一系列相互平行的坐标轴表示, 纵向是属性值,横向是属性类别。
- 若在某个属性上相同颜色折线较为集中,不同颜色有一定的间距,则说明该属性对于预标签类别判定有较大的帮助。
- 若某个属性上线条混乱,颜色混杂,则可能该属性对于标签类别判定没有价值。
plotting.parallel_coordinates(df.drop('CustomerID', axis=1), 'Gender')
plt.title('平行坐标图', fontsize=12)
plt.grid(linestyle='-.')
plt.show()
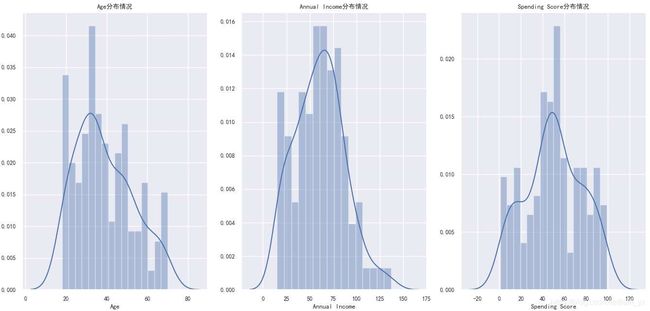
2.2 年龄/年收入/消费分数的分布
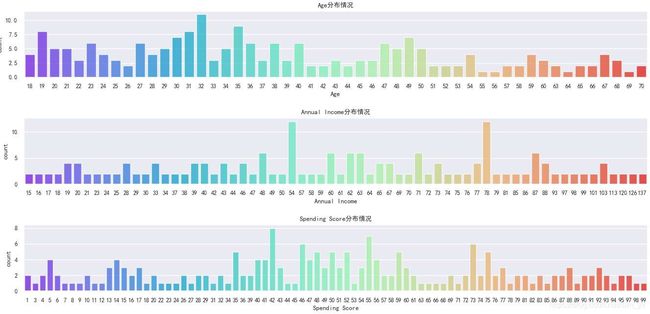
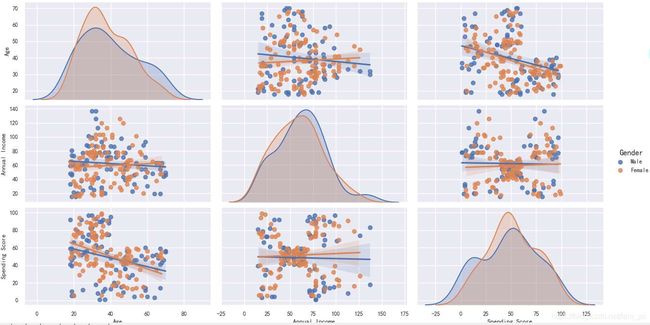
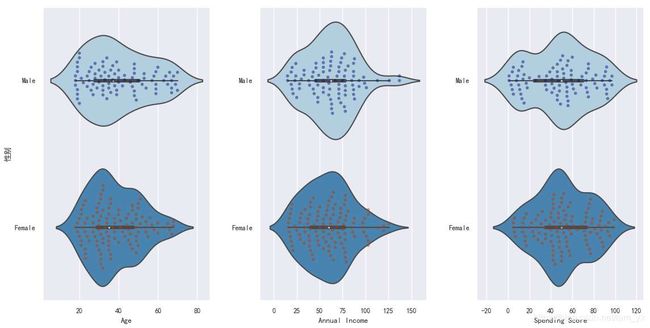
这里用了直方图和核密度图。(注:核密度图看的是(x 如下图。从左到右分别是年龄、年收入和消费能力的分布情况。发现: 2.3年龄/年收入/消费分数的柱状图 这里使用的是柱状图,和直方图不同的是: x xx轴上的每一个刻度对应的是一个离散点,而不是一个区间。 如下图。从上到下分别是年龄、年收入和消费能力的柱状图。发现: 2.4不同性别用户占比 如下饼图。女性以56%的份额居于领先地位,而男性则占整体的44%。特别是当男性人口相对高于女性时,这是一个比较大的差距。 2.5 两两特征之间的关系 pairplot主要展现的是属性(变量)两两之间的关系(线性或非线性,有无较为明显的相关关系)。注意,我对男、女性的数据点进行了区分(但是感觉数据在性别上的差异不大呀?)。如下组图所示: 2.6 两两特征之间的分布 其实,下面这一部分也包含了上面的信息。 四、K-means聚类分析 0.手肘法简介 核心指标 误差平方和(sum of the squared errors,SSE)是所有样本的聚类误差反映了聚类效果的好坏,公式如下: 核心思想 1.基于年龄和消费分数的聚类 所需要的数据有‘Age'和‘Spending Score'。 使用手肘法确定最合适的 k kk值。 绘图确定 k kk值,这里将 k kk确定为4。 通过如下图,确定 k kk=4。 确定 k kk=4后。重新构建 k kk=4的K-means模型,并且绘制聚类图。 效果如下,基于年龄和消费能力这两个参数,可以将用户划分成4类。 2.基于年收入和消费分数的聚类 所需要的数据 同理,使用手肘法确定合适的 k kk值。 通过如下图,确定 k kk=5。 确定 k kk=5后。重新构建 k kk=5的K-means模型,并且绘制聚类图 效果如下,基于年收入和消费能力这两个参数,可以将用户划分成如下5类: 3.基于年龄、收入和消费分数的聚类所需要的数据 聚类, k kk=5。 绘图。 效果如下。 五、小结 到此这篇关于Python用K-means聚类算法进行客户分群的实现的文章就介绍到这了,更多相关Python K-means客户分群内容请搜索脚本之家以前的文章或继续浏览下面的相关文章希望大家以后多多支持脚本之家!
sns.set(palette="muted", color_codes=True) # seaborn样式
# 配置
plt.rcParams['axes.unicode_minus'] = False # 解决无法显示符号的问题
sns.set(font='SimHei', font_scale=0.8) # 解决Seaborn中文显示问题
# 绘图
plt.figure(1, figsize=(13, 6))
n = 0
for x in ['Age', 'Annual Income', 'Spending Score']:
n += 1
plt.subplot(1, 3, n)
plt.subplots_adjust(hspace=0.5, wspace=0.5)
sns.distplot(df[x], bins=16, kde=True) # kde 密度曲线
plt.title('{}分布情况'.format(x))
plt.tight_layout()
plt.show()
plt.figure(1, figsize=(13, 6))
k = 0
for x in ['Age', 'Annual Income', 'Spending Score']:
k += 1
plt.subplot(3, 1, k)
plt.subplots_adjust(hspace=0.5, wspace=0.5)
sns.countplot(df[x], palette='rainbow', alpha=0.8)
plt.title('{}分布情况'.format(x))
plt.tight_layout()
plt.show()
df_gender_c = df['Gender'].value_counts()
p_lables = ['Female', 'Male']
p_color = ['lightcoral', 'lightskyblue']
p_explode = [0, 0.05]
# 绘图
plt.pie(df_gender_c, labels=p_lables, colors=p_color, explode=p_explode, shadow=True, autopct='%.2f%%')
plt.axis('off')
plt.legend()
plt.show()
# df_a_a_s = df.drop(['CustomerID'], axis=1)
sns.pairplot(df, vars=['Age', 'Annual Income', 'Spending Score'], hue='Gender', aspect=1.5, kind='reg')
plt.show()
kind 参数设置为 reg 会为非对角线上的散点图拟合出一条回归直线,更直观地显示变量之间的关系。
# 根据分类变量分组绘制一个纵向的增强箱型图
plt.rcParams['axes.unicode_minus'] = False # 解决无法显示符号的问题
sns.set(font='SimHei', font_scale=0.8) # 解决Seaborn中文显示问题
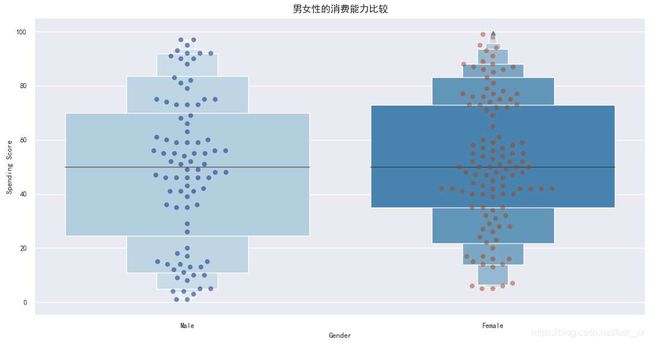
sns.boxenplot(df['Gender'], df['Spending Score'], palette='Blues')
# x:设置分组统计字段,y:数据分布统计字段
sns.swarmplot(x=df['Gender'], y=df['Spending Score'], data=df, palette='dark', alpha=0.5, size=6)
plt.title('男女性的消费能力比较', fontsize=12)
plt.show()
# 根据分类变量分组绘制一个纵向的增强箱型图
plt.rcParams['axes.unicode_minus'] = False # 解决无法显示符号的问题
sns.set(font='SimHei', font_scale=0.8) # 解决Seaborn中文显示问题
sns.boxenplot(df['Gender'], df['Spending Score'], palette='Blues')
# x:设置分组统计字段,y:数据分布统计字段
sns.swarmplot(x=df['Gender'], y=df['Spending Score'], data=df, palette='dark', alpha=0.5, size=6)
plt.title('男女性的消费能力比较', fontsize=12)
plt.show()
df_a_sc = df[['Age', 'Spending Score']].values
# 存放每次聚类结果的误差平方和
inertia1 = []
for n in range(1, 11):
# 构造聚类器
km1 = (KMeans(n_clusters=n, # 要分成的簇数,int类型,默认值为8
init='k-means++', # 初始化质心,k-means++是一种生成初始质心的算法
n_init=10, # 设置选择质心种子次数,默认为10次。返回质心最好的一次结果(好是指计算时长短)
max_iter=300, # 每次迭代的最大次数
tol=0.0001, # 容忍的最小误差,当误差小于tol就会退出迭代
random_state=111, # 随机生成器的种子 ,和初始化中心有关
algorithm='elkan')) # 'full'是传统的K-Means算法,'elkan'是采用elkan K-Means算法
# 用训练数据拟合聚类器模型
km1.fit(df_a_sc)
# 获取聚类标签
inertia1.append(km1.inertia_)
plt.figure(1, figsize=(15, 6))
plt.plot(np.arange(1, 11), inertia1, 'o')
plt.plot(np.arange(1, 11), inertia1, '-', alpha=0.7)
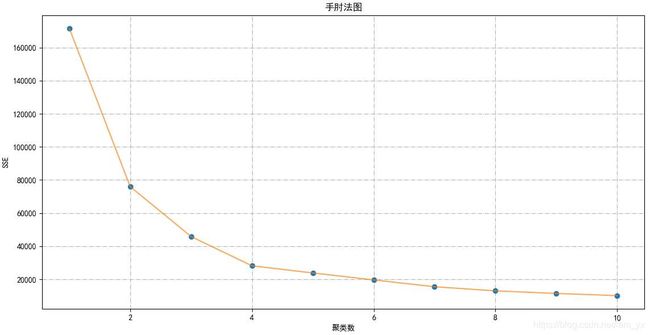
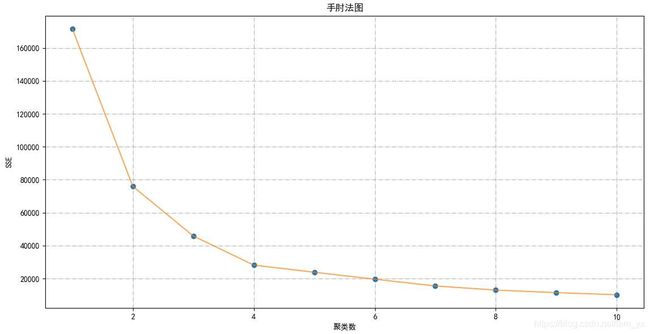
plt.title('手肘法图', fontsize=12)
plt.xlabel('聚类数'), plt.ylabel('SSE')
plt.grid(linestyle='-.')
plt.show()
km1_result = (KMeans(n_clusters=4, init='k-means++', n_init=10, max_iter=300,
tol=0.0001, random_state=111, algorithm='elkan'))
# 先fit()再predict(),一次性得到聚类预测之后的标签
y1_means = km1_result.fit_predict(df_a_sc)
# 绘制结果图
plt.scatter(df_a_sc[y1_means == 0][:, 0], df_a_sc[y1_means == 0][:, 1], s=70, c='blue', label='1', alpha=0.6)
plt.scatter(df_a_sc[y1_means == 1][:, 0], df_a_sc[y1_means == 1][:, 1], s=70, c='orange', label='2', alpha=0.6)
plt.scatter(df_a_sc[y1_means == 2][:, 0], df_a_sc[y1_means == 2][:, 1], s=70, c='pink', label='3', alpha=0.6)
plt.scatter(df_a_sc[y1_means == 3][:, 0], df_a_sc[y1_means == 3][:, 1], s=70, c='purple', label='4', alpha=0.6)
plt.scatter(km1_result.cluster_centers_[:, 0], km1_result.cluster_centers_[:, 1], s=260, c='gold', label='质心')
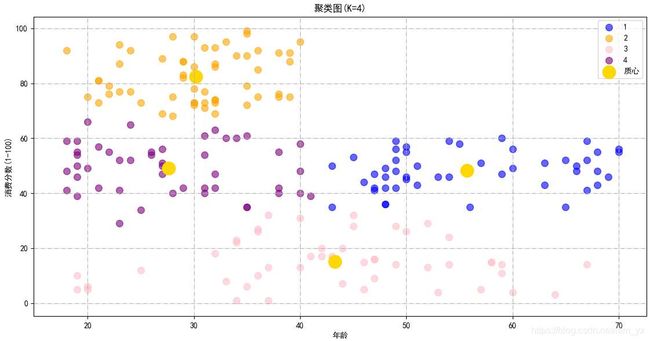
plt.title('聚类图(K=4)', fontsize=12)
plt.xlabel('年收入(k$)')
plt.ylabel('消费分数(1-100)')
plt.legend()
plt.grid(linestyle='-.')
plt.show()
df_ai_sc = df[['Annual Income', 'Spending Score']].values
# 存放每次聚类结果的误差平方和
inertia2 = []
for n in range(1, 11):
# 构造聚类器
km2 = (KMeans(n_clusters=n, init='k-means++', n_init=10, max_iter=300, tol=0.0001, random_state=111, algorithm='elkan'))
# 用训练数据拟合聚类器模型
km2.fit(df_ai_sc)
# 获取聚类标签
inertia2.append(km2.inertia_)
# 绘制手肘图确定K值
plt.figure(1, figsize=(15, 6))
plt.plot(np.arange(1, 11), inertia1, 'o')
plt.plot(np.arange(1, 11), inertia1, '-', alpha=0.7)
plt.title('手肘法图', fontsize=12)
plt.xlabel('聚类数'), plt.ylabel('SSE')
plt.grid(linestyle='-.')
plt.show()
km2_result = (KMeans(n_clusters=5, init='k-means++', n_init=10, max_iter=300,
tol=0.0001, random_state=111, algorithm='elkan'))
# 先fit()再predict(),一次性得到聚类预测之后的标签
y2_means = km2_result.fit_predict(df_ai_sc)
# 绘制结果图
plt.scatter(df_ai_sc[y2_means == 0][:, 0], df_ai_sc[y2_means == 0][:, 1], s=70, c='blue', label='1', alpha=0.6)
plt.scatter(df_ai_sc[y2_means == 1][:, 0], df_ai_sc[y2_means == 1][:, 1], s=70, c='orange', label='2', alpha=0.6)
plt.scatter(df_ai_sc[y2_means == 2][:, 0], df_ai_sc[y2_means == 2][:, 1], s=70, c='pink', label='3', alpha=0.6)
plt.scatter(df_ai_sc[y2_means == 3][:, 0], df_ai_sc[y2_means == 3][:, 1], s=70, c='purple', label='4', alpha=0.6)
plt.scatter(df_ai_sc[y2_means == 4][:, 0], df_ai_sc[y2_means == 4][:, 1], s=70, c='green', label='5', alpha=0.6)
plt.scatter(km2_result.cluster_centers_[:, 0], km2_result.cluster_centers_[:, 1], s=260, c='gold', label='质心')
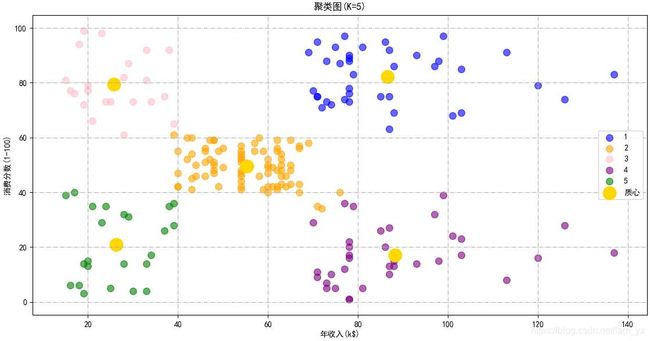
plt.title('聚类图(K=5)', fontsize=12)
plt.xlabel('年收入(k$)')
plt.ylabel('消费分数(1-100)')
plt.legend()
plt.grid(linestyle='-.')
plt.show()
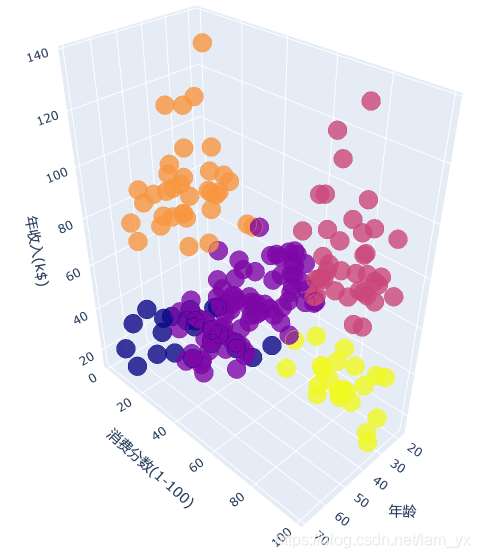
df_a_ai_sc = df[['Age', 'Annual Income', 'Spending Score']].values
km3 = KMeans(n_clusters=5, init='k-means++', max_iter=300, n_init=10, random_state=0)
km3.fit(df_a_ai_sc)
df['labels'] = km3.labels_
# 绘制3D图
trace1 = go.Scatter3d(
x=df['Age'],
y=df['Spending Score'],
z=df['Annual Income'],
mode='markers',
marker=dict(
color=df['labels'],
size=10,
line=dict(
color=df['labels'],
width=12
),
opacity=0.8
)
)
df_3dfid = [trace1]
layout = go.Layout(
margin=dict(
l=0,
r=0,
b=0,
t=0
),
scene=dict(
xaxis=dict(title='年龄'),
yaxis=dict(title='消费分数(1-100)'),
zaxis=dict(title='年收入(k$)')
)
)
fig = go.Figure(data=df_3dfid, layout=layout)
py.offline.plot(fig)