食物链 POJ - 1182 带权并查集 （不一样的做法）

食物链

法一、

今天在《挑战程序设计竞赛》中看到对于这题一种独特的写法，巧妙应用了并查集，于是理解后摘抄下来分享一下。

由于N和K很大，所以必须高效地维护动物之间的关系，并快速判断是否产生了矛盾。并查集是维护 “属于同一组” 的数据结构，但是在本题中，并不只有属于同一类的信息，还有捕食关系的存在。因此需要开动脑筋维护这些关系。

对于每只动物i创建3个元素i-A, i-B, i-C, 并用这3*N个元素建立并查集。这个并查集维护如下信息：

① i-x 表示 “i属于种类x”。

②并查集里的每一个组表示组内所有元素代表的情况都同时发生或不发生。

例如，如果i-A和j-B在同一个组里，就表示如果i属于种类A那么j一定属于种类B，如果j属于种类B那么i一定属于种类A。因此，对于每一条信息，只需要按照下面进行操作就可以了。

1）第一种，x和y属于同一种类———合并x-A和y-A、x-B和y-B、x-C和y-C。

2）第二种，x吃y—————————合并x-A和y-B、x-B和y-C、x-C和y-A。

不过在合并之前需要先判断合并是否会产生矛盾。例如在第一种信息的情况下，需要检查比如x-A和y-B或者y-C是否在同一组等信息。（一开始我一直不明白，对于两种信息都是合并，那么以后怎么分清到底是同类还是捕食关系呢，或者说如何判断是否会产生矛盾呢？后来发现，它利用3*N的数组分3段1~N,N~2N,2N~3N分别当做是A、B、C三个种类的集合，把所有可能符合的情况都会导入进去，虽然对于两种信息的操作都是合并，但合并的内容是不一样的，这样就可以在合并之前判断其是否以另一种信息合并过或者符合另一种信息。可以自己举例来理解一下）

#include
#include
const int maxn=50005;
int pre[3*maxn];   
int find(int x)
{
    return pre[x]==x?x:pre[x]=find(pre[x]);
}
int same(int x,int y)
{
    if(find(x)==find(y))
        return 1;
    return 0;
}
void merge(int x,int y)
{
    x=find(x),y=find(y);
    if(x!=y)
        pre[x]=y;
}
int main()
{
    int n,k,d,x,y;
    scanf("%d%d",&n,&k);
    for(int i=0;i<=3*n;i++)   //元素x，x+N，x+2*N分别代表x-A，x-B，x-C
        pre[i]=i;
    int cnt=0;
    for(int i=0;in||y<0||y>n)
        {
            cnt++;
            continue;
        }
        if(d==1)           //d==1时，x和y为同类，不可能出现捕食或被捕食关系
        {
            if(same(x,y+n)||same(x,y+2*n))
                cnt++;
            else             //因为不知道x，y为A,B,C中的哪一类  所以全部加入
            {
                merge(x,y);
                merge(x+n,y+n);
                merge(x+2*n,y+2*n);
            }
        }
        else         //当d==2时，x和y不可能是同类 或 被捕食关系  
        {
           if(same(x,y)||same(x,y+2*n))    
                cnt++;
           else          //因为不知道x，y为A,B,C中的哪一类，所以存在捕食关系的全部加入
           {
               merge(x,y+n);
               merge(x+n,y+2*n);
               merge(x+2*n,y);
           }
        }
    }
    printf("%d\n",cnt);
    return 0;
}

法二、

带权并查集。

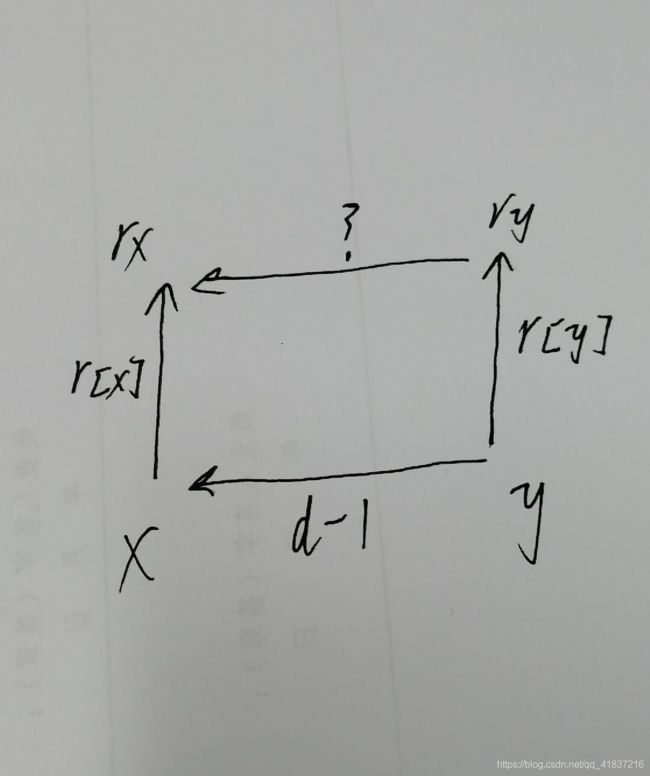
合并前（不再同一集合）的关系图（此处将 pre[ry]=rx，将 y 所在的集合并入 x 所在的集合，不同的并入方式对应的向量图不同 ）。满足关系：r[ry] = ( r[x]+(d-1) - r[y]+3 )%3

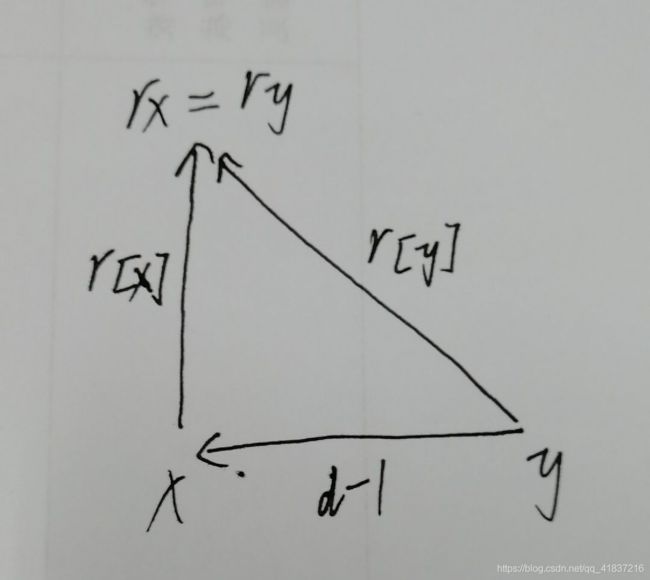
合并后（在同一集合）的关系图，满足关系：( r[y] - r[x] + 3 )%3 = d-1

解析

 

#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include

 

这是我的一点见解，如果文中有误或有更好的见解  请多多指教 q(≧▽≦q)

本文参考博客

https://blog.csdn.net/sunmaoxiang/article/details/80959300

https://blog.csdn.net/jxust_tj/article/details/43668901

https://blog.csdn.net/qq_33583069/article/details/53053856