数据结构与算法C++描述(1)---线性表的基本操作
本文将利用公式化描述的方法,借助于C++语言,建立线性表,实现线性表的创建、删除、元素插入、线性表的合并与拆分等操作。
文中所有代码皆上传至我的码云
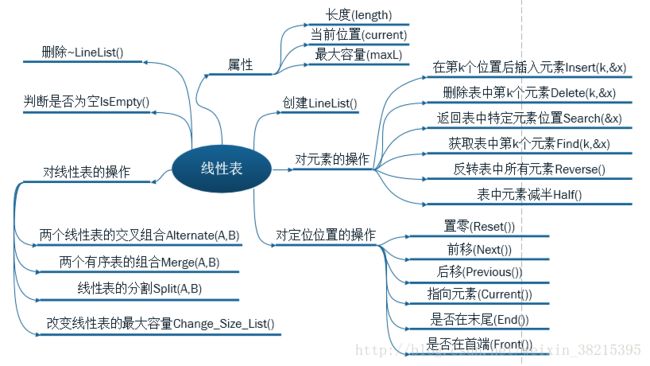
1、 线性表的定义
在参考文献[1]中,对线性表有如下定义:线性表(linear list)是这样的数据对象,其实例形式为:(e1,e2,…,en),其中n是有穷自然数。ei是表中的元素,n是表的长度。元素可以被视为原子,因为它们本身的结构与线性表的结构无关。当n=0时,表为空;当n>0时,e1是第一个元素,en是最后一个元素,可以认为e1优先于e2,e2优先于e3,如此等等。除了这种优先关系之外,在线性表中不再有其他的结构。
2、线性表的相关操作
3、线性表各种操作的C++实现
将线性表抽象为LineLiset()类,通过成员函数实现对线性表的各种操作。LineList类具有四个私有变量:
T *element; //模板类,动态一维数组
int MaxL; //最大长度
int length; //数组长度
int current; //元素当前位置3.1 创建线性表
利用LineList类的构造函数创建线性表。
//构造函数,创建初始表
template <class T> //模板类
LineList::LineList()
{
MaxL=1; //初始表长度最大容量为1
element=new T[MaxL];
length=0; //长度为0
} 3.2 删除线性表
通过LineList类的析构函数删除线性表。
//析构函数,删除表
template <class T> //模板类
LineList::~LineList()
{
delete [] element;
} 3.3 判断线性表是否为空
通过LineList类的公共成员函数IsEmpty()判断线性表是否为空。
//判断数组是否为空:是,则返回true
template <class T> //模板类
bool LineList::IsEmpty() const
{
return length==0;
} 3.4 对元素的操作
对线性表中元素的操作包括:
3.4.1 插入元素
由于在创建线性表时,为了节省空间,建立的初始线性表的长度为0,随着线性表元素的增减,线性表的最大容量maxL也会随着变化。变化规则为:当线性表的长度length==maxL时,将maxL扩大为原来的两倍,及maxL=2*maxL;当length=maxL/4时,将maxL缩小为原来的1/2,即maxL=maxL/2。当maxL变化后,建立一个新的线性表,并将原来的线性表中的数据复制给新线性表后,删除原来的额线性表。
在第k个位置后插入元素x,并返回修改后的线性表,通过公共成员函数LineList实现;
//在第k个元素之后插入x;函数返回修改后的线性表
template
LineList& LineList::Insert(int k,const T &x)
{
//不存在第k个元素,抛出异常
if(k<0 || k>length) throw OutOfRange();
if(length==MaxL) throw NoMem();
for(int i=length-1;i>=k;i--)
element[i+1]=element[i];
element[k]=x;
length++;
if(length==MaxL)
{
MaxL=MaxL*2;
Change_Size_List(element,length,MaxL); //改变线性表的最大容量
}
return *this;
} 代码说明:
(1)在上述代码中,有两个异常类OutOfRange()和NoMem(),分别表示超出线性表的最大容量和内存不足。此后的代码中也将会用到这两个异常。其声明如下:
#include//使new引发NoMemory异常而不是xalloc异常
void my_new_handler()
{
throw NoMem();
}
new_handler Old_Handler_=set_new_handler(my_new_handler);
//超出范围
class OutOfRange{
public:
OutOfRange(){};
~OutOfRange(){};
}; (2)代码中的Change_Size_List(element,length,MaxL);函数,参数分别代表:LineList的当前数组element,当前长度,增减后的最大容量MaxL。具体的函数实现如下:
template <class T>
LineList& LineList::Change_Size_List(T *element_new,int l,int m)
{
element=new T[m];
for(int i=0;idelete [] element_new;
return *this;
} (3)关于*this指针:this指针里面存储着当前LineList类中的内容,包括公共成员和私有成员以及保护成员,它在构造函数运行之前建立,在析构函数运行之后便被销毁,也就是说,它只存在于具体的类的对象中。
3.4.2 删除元素
删除表中第k个元素,并把它保存到x中,返回修改后的线性表,通过公共成员函数LineList实现;
//删除表中第k 个元素,并把它保存到x 中;函数返回修改后的线性表
template
LineList& LineList::Delete(int k,T &x)
{
if(Find(k,x))
{
for(int i=k-1;i<length;i++)
element[i]=element[i+1];
length--;
if(length==(MaxL/4) && length>0)
{
MaxL=MaxL/2;
Change_Size_List(element,length,MaxL);
}
return *this;
}
else
throw OutOfRange();
}
3.4.3 获取元素位置
获取表中元素x的位置,若不存在此元素则返回0,通过公共成员函数int Search(const T &x) const;实现;
//返回元素x在表中的位置;如果x 不在表中,则返回0
template <class T>
int LineList::Search(const T &x) const
{
for(int i=1;i<=length;i++)
{
if(element[i-1]==x)
return i;
}
return 0;
} 3.4.4 获取表中元素
获取线性表中第k个元素,并把它赋值给x,若不存在第k个元素,则返回false,通过公共成员函数bool Find(int k,T &x) const;实现;
//寻找表中第k个元素,并把它赋给x,若不存在第k个元素,则返回false
template <class T>
bool LineList::Find(int k,T &x) const
{
if(k<0 || k>length)
return false;
else
x=element[k-1];
} 3.4.5 元素反转
反转线性表中的元素,通过公共成员函数LineList实现;
//数据反转函数
template
LineList& LineList::Reverse()
{
for(int i=0;i<(length/2);i++)
{
int temp=element[i];
element[i]=element[length-1-i];
element[length-1-i]=temp;
}
return *this;
} 3.4.6 元素减半
线性表中的元素减半,只保留奇数位置上的元素,通过公共成员函数LineList实现;
//数据减半函数
template
LineList& LineList::Half()
{
length=(length+1)/2;
T *element_new=new T[length+1];
for(int i=0;i<=length;i++)
element_new[i]=element[2*i];
delete [] element;
element=new T [length+1];
for(int i=0;i<=length;i++)
element[i]=element_new[i];
delete [] element_new;
return *this;
} 3.5 对定位位置的操作
通过声明LineLiset类的私有变量current,指向线性表的位置坐标。那么,对位置坐标的操作有:置零(位置清零)、指向下一个位置、指向前一个位置、获取当前位置上的元素、判断是否在线性表的首端以及是否在线性表的末端。具体实现如下:
//元素位置相关函数
void Reset(){current=0;}; //置零current
bool Current(T &x){ //返回当前位置的元素,给x
if(current<=0 || current>length) return false;
else{
x=element[current-1];
return true;
}
}
bool End(){return current==length;}; //是否在最后
bool Front(){return current==1;}; //是否在最前面
void Next() { //移至下一个元素
if(current<length)
current++;
else
throw OutOfRange();
};
void Previous(){ //移至前一个元素
if(current>1)
current--;
else
throw OutOfRange();
}3.6 对多个线性表的操作
对多个线性表的操作主要有:对两个线性表的交叉组合、对两个有序表的组合、线性表的分割。
3.6.1 两个线性表的交叉组合
两个线性表的交叉组合是指:已知两个线性表A和B,将A和B中的元素交叉排列组成线性表L,即:L的首位置上放A的第一个元素,第二个位置上放B的第一个元素,第三个位置上放A的第二个元素,依次循环放置,当一个线性表的元素全部放完,则L的余下位置上依次放置另一个线性表的剩余元素,直到将所有元素放至L中。具体实现如下:
//线性表的交叉组合
template <class T>
LineList& LineList::Alternate(const LineList &A,const LineList &B)
{
length=A.Length()+B.Length();
element=new T[length];
A.Reset(); //位置置0
B.Reset(); //位置置0
int x; //当前位置上的元素
int min_l=A.Length(); //A和B中的最小长度
if(min_l>B.Length())
min_l=B.Length();
for(int i=0;i//移至下一个元素
if(A.Current(x))
element[2*i]=x;
B.Next(); //移至下一个元素
if(B.Current(x))
element[2*i+1]=x;
}
//经过上述current的移动,现在current在较短的线性表末端
for(int i=2*min_l;iif(!A.End()) //如果不是在A的末端,说明A线性表较长,则将A中后面元素依次赋给新线性表
{
A.Next();
A.Current(x);
element[i]=x;
}
else{ //否则,说明A线性表较短,则将B中后面元素依次赋给新线性表
B.Next();
B.Current(x);
element[i]=x;
}
}
return *this;
} 3.6.2 两个有序线性表的组合
所谓两个有序表的组合是指,已知两个线性表A和B中的元素都是有序排列(如都是从小到大依次排列),将两者组合成线性表L后,L中的元素也是有序的(如从小到大排列)。具体实现如下:
//有规律(元素从小到大排列)线性表的组合
template<class T>
LineList& LineList::Merge(const LineList &C,const LineList &D)
{
length=C.Length()+D.Length();
element=new T [length];
int ca=0,cb=0,ct=0; //A、B、L的索引值
while (caif(C.element[ca]>=D.element[cb])
element[ct++]=D.element[cb++];
else
element[ct++]=C.element[ca++];
}
if(ca==C.Length()) //说明A已经判断完
{
for(int i=cb;ielse //说明A没判断完
{
for(int i=ca;ireturn *this;
} 3.6.3 线性表的分割
所谓线性表的分割是指:已知线性表L,将其分割为线性表A和B,其中A和B中的元素有一下特点:A中的第一个元素为L中的第一个元素,B中元素为L中的第二个元素,A中的第二个元素为L中的第三个元素,依次类推,直到将L中的元素分完。此问题可看成“两个线性表的交叉组合的逆问题”。具体实现如下:
//线性表的分割
template
void LineList::Split(LineList &A, LineList &B)
{
int ca=0,cb=0,i;
for(i=0;i<(length/2);i++)
{
B.Insert(cb,element[2*i]);
cb++;
A.Insert(ca,element[2*i+1]);
ca++;
}
if((2*i-1)<=(length-1)) //原线性表有奇数个元素
B.Insert(cb,element[length-1]);
} 4、线性表的输出
通过重载输出运算符“<<”,实现对线性表的输出。
//输出
template <class T>
void LineList::Output(ostream &out) const
{//把表送至输出流
for(int i=0;iout<" ";
}
//重载<<
template <class T>
ostream & operator<<(ostream &out,const LineList& x)
{
x.Output(out);
return out;
} 5、测试数据
现在越发觉得一个好的测试数据集对于一个程序是非常重要的。对于程序的测试,总体来说,主要要做到以下两点:
- 要让程序的每条语句都至少运行一次;
特殊情况的分析考虑。
针对以上建立的LineList类,设计了以下测试数据:
/**
* 李震
* 我的码云:https://git.oschina.net/git-lizhen
* 我的CSDN博客:http://blog.csdn.net/weixin_38215395
* 联系:QQ1039953685
*/
try{
cout<<"原始空线性表: "<int> L;
cout<<"Length="<cout<<"IsEmpty="<cout<"依次插入5个数据后: "<0,2).Insert(1,5).Insert(2,3).Insert(3,1).Insert(4,-10);
cout<<"List is "<cout<<"IsEmpty="<cout<<"Length="<cout<"测试Insert(): "<1,10).Insert(2,100);
cout<<"List is "<cout<<"Length="<cout<"测试Delete(): "<int x;
L.Delete(1,x);
cout<<"List is "<cout<<"Length="<cout<"测试Search(): "<cout<<"List is "<cout<<"5 in L? "<5)<cout<<"2 in L? "<2)<cout<"测试Reverse()---偶数个数据: "<cout<<"List is "<cout<<"Length="<cout<<"测试Reverse()---奇数个数据: "<1,x);
cout<"删除一个数据后:List is "<cout<<"List is "<cout<<"Length="<11,10);
cout<"测试Insert(): "<cout<<"List is "<cout<<"Length="<//反转测试
for(int i=0;i<5000000;i++)
L.Insert(i,i);
cout<<"Length="<//类的成员函数实现数据反转
clock_t start_time,stop_time;
start_time=clock();
//计算执行时间
L.Reverse();
stop_time=clock();
cout<<"类的成员函数实现数据反转:"<<float(stop_time-start_time)/CLK_TCK<//就地反转
clock_t start_time_main,stop_time_main;
start_time_main=clock();
//计算执行时间
Reverse_main(L);
stop_time_main=clock();
cout<<"就地实现数据反转:"<<float(stop_time_main-start_time_main)/CLK_TCK<//测试Half()函数
//空数组
cout<<"空数组: "<cout<<"List is "<cout<<"IsEmpty="<cout<<"Length="<//有奇数个数
cout<"依次插入5个数据后: "<0,2).Insert(1,5).Insert(2,3).Insert(3,1).Insert(4,-10);
cout<<"List is "<cout<<"减半后:List is "<cout<<"List is "<cout<<"IsEmpty="<cout<<"Length="<//有偶数个数
cout<"依次插入第6个数据后: "<1,9);
cout<<"List is "<cout<<"减半后:List is "<cout<<"IsEmpty="<cout<<"Length="<//测试current
for(int i=0;i<10;i++)
L.Insert(i,i);
cout<"List is: "<//置0
//测试Next()函数
L.Next(); //移至下一个元素
cout<<"是否在最前?"<int x;
L.Current(x);
cout<<"移至下一个元素后,当前元素: "<//移至下一个元素
L.Current(x);
cout<<"移至下一个元素后,当前元素: "<//测试Previous()函数
L.Previous(); //移至上一个元素
L.Current(x);
cout<<"移至上一个元素后,当前元素: "<//测试End()函数
for(int i=0;i<9;i++)
L.Next(); //移至下一个元素
L.Current(x);
cout<<"后移九次后,当前元素: "<cout<<"是否在最后?"<//测试Alternate()函数
LineList<int> A,B;
//产生测试数据
for(int i=0;i<4;i++) //生成等长的A和B
{
A.Insert(i,2*i);
B.Insert(i,2*i-1);
}
int i=5;
while(i>0) //将B加长
{
B.Insert(4,10);
i--;
}
cout<<"线性表A为: "<cout<<"线性表B为: "<//测试
L.Alternate(A,B);
cout<<"A在前,B在后,交叉组合后线性表L为: "<cout<<"B在前,A在后,交叉组合后线性表L为: "<//测试Merge()函数
LineList<int> A,B;
//产生测试数据
for(int i=0;i<4;i++) //生成等长的A和B
{
A.Insert(i,2*i);
B.Insert(i,2*i-1);
}
int i=5;
while(i>0) //将B加长
{
B.Insert(4,10);
i--;
}
cout<<"线性表A为: "<cout<<"线性表B为: "<//测试
L.Merge(A,B);
cout<<"A在前,B在后,组合后线性表L为: "<cout<<"B在前,A在后,组合后线性表L为: "<//测试Split()函数
//产生测试数据
for(int i=0;i<10;i++) //生成等长的A和B
{
L.Insert(i,i);
}
LineList<int> A,B;
//原始线性表有偶数个数据
L.Split(A,B);
cout<<"原始线性表为: "<cout<<"分割后线性表A为: "<cout<<"分割后线性表B为: "<//原始线性表有奇数个数据
L.Insert(10,10);
L.Split(A,B);
cout<<"原始线性表为: "<cout<<"分割后线性表A为: "<cout<<"分割后线性表B为: "<catch(NoMem){
cerr<<"No Memory!!!"<catch(OutOfRange){
cerr<"Out Of Range!!!"< 下一节将介绍数据的另一种描述方法:链表
数据结构C++描述—链表
参考文献:
[1] 数据结构算法与应用:C++描述(Data Structures, Algorithms and Applications in C++ 的中文版)