《数据结构》002线性结构—— 0A 线性表
链表的创建 使用
例一:一元多项式
顺序存储的线性表示:
1、顺序存储结构直接表示:数组
(按指数大小有序存储) 
2、顺序存储结构表示非零项:结构数组:(系数,指数)

加法运算实现:

3、链表结构存储非零项
链表中每个节点存储多项式中的一个非零项,包括叙述和指数两个数据与以及一个指针域

typedef struct PolyNode *Polynomial;
struct PolyNode{
int coef;
int expon;
Polynomial link;
} #然后进行加法运算
线性表:
定义: 由同类型数据元素构成的有序序列的线性结构
元素个数—>线性表长度
空表
线性表 L ∈ List, 整数 i 表示位置, 元素 X ∈ ElementTyp (可以为int char )
存储方法:
(一)数组: 利用数组的连续存储空间顺序存放线性表的各元素
定义方法:typedef struct LNode *LIst; struct LNode{ ElementType Data[MAXSIZE]; int Last; }; struct LNode L; List PtrL;
访问元素: List.Data[1] //错误!
L.Data[1] 或者 PtrL->Last+1
线性表长度: L.Last+1 或者 PtrL->Last+1
主要操作和实现
1、初始化:建立空的顺序表
数组 Last
List MakeEmpty()
{
List PtrL;
PtrL = ( List ) malloc ( sizeof( struct LNode ) );
PtrL-> Last = -1; //最后一个元素
return PtrL;
}
2、查找:
int Find( ElementType X, List PrtL)
{
int i = 0;
while( i <= PtrL->Last && PtrL->Data[i] = X)
i++;
if (i > PtrL->Last) return -1; //未找到,返回-1
else return i; //找到,返回位置 i
}
3、插入: 从后向前先移动
定义循环变量数值 判断是否可插入 (表满?位置对?) for循环依次向后移动移动 插入数值 更改表的长度 Last指针值
void Insert( ElementType X, int i, List PtrL )
{
int j;
if( PtrL->Last == MAXSIZE - 1)
{
cout<<"表满!";
return ;
}
if( i < 1 || i == MAXSIZE + 2) // 因为插入的元素是位置 i, 不是下标 i
{
cout<<"位置不合法!";
return;
}
for( j = PtrL->Last; j >= i-1; j --) // 原下标为 [ i-1, j] 的元素统统向后移
PtrL->Data[j+1] = PtrL->Data[j];
PtrL->Data[i-1] = X;
PtrL->Last++;
return;
}
#问:如果把后移数组元素的循环
for ( j = PtrL->Last; j >= i-1; j-- )
PtrL->Data[j+1]=PtrL->Data[j];
改为
for ( j = i-1; j <= PtrL->Last; j++ )
PtrL->Data[j+1]=PtrL->Data[j];
#结果会怎样?
答: Data[i] 至 Dataj 的值都相同,且都为 Data[i-1]
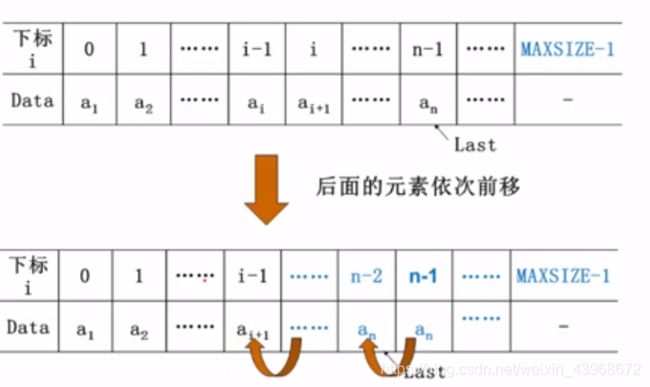
void Delete( int i, List PtrL )
{
int j;
if( i < 1 || i > PtrL->Last+1)
{
cout<<"位置不合法!";
return ;
}
for( j = i; j <= PtrL->Last; j++)
PtrL->Data[j] =PtrL-> Data[j-1];
PtrL->Last--;
return;
}
(二)链式存储实现
不要求逻辑上相邻的两个元素物理上也相邻, 插入、删除不需要移动元素,只需要修改链
链表的定义:
typrdef struct LNode *List; // 这个定义是什么意思? 以后什么时候该用List ,LNode
struct LNode
{
ElementType Data;
List Next;
};
struct LNode L; // L 干嘛的?
List PtrL; //此处,LNode 与 List有何区别?
主要操作:
1、求表长: while 语句遍历
int Length( List PtrL)
{
List p = PtrL; //头指针不能随便移动 金蝉脱壳 临时
int j = 0;
while(p)
{
p = p->Next; //如果光是 p->Next; 会哪样?
j++;
}
return j;
}
2、查找:
(1)按序号 FindKth 查找
根据序号(值不为空 且 i 的取值小于 K)查找 判断 i 的值是否符合 位置K,若符合,则返回指针p(否则为错误,未找到)
List FindKth( int K, List PtrL )
{
List p = PtrL;
int i =1;
while( p != NULL && i < K)
{
p = p->Next;
i++;
}
if( i == K) //找到第 K 个,返回指针
return p;
else
return NULL;
}
(2)按值 Find 查找:
根据给出的值遍历( 指针非空且值不为X ) 返回指针
List Find(ElementType X, List PtrL)
{
List p = PtrL;
while( p != NULL;&& p->Data != X)
p = p->Next;
return p;
}
3、插入
方法:
(1)首先用 malloc 函数构造一个新的指针 s
(2)找到要插入的第 i-1 个节点,用 p 指向
(3)修改指针
判断插在哪里(表头 表身 表尾 (它前面的第 i-1 个节点) )
List Insert( ElementType X, int i, List PtrL)
{
List s, p;
if( i == 1)
// 新节点在表头插入 0 的位置在链表中不存在 头指针变化 所以可以
{
s = (List)malloc( sizeof(struct LNode) ); // 申请填装节点
s->Data = X;
s->Next = PtrL;
return s;
}
p = FindKth(i-1, PtrL); //用指针 p 查找第 i-1 个节点
if( p == NULL) // 不存在, 参数 i 错
{
cout<<" 参数 i 错误!";
}
return NULL;
else
{
s = (LIst)malloc(sizeof(struct LNode) ) // 申请 填装节点
s->Data = X;
s->Next = p->Next;
p->Next = s;
return PtrL;
}
4.删除:
方法:
(1)找到第 i-1 个节点,p 指向、
(2)s 指向下一个,也就是要被删除的节点
(3)修改指针
(4)释放 s 空间
LIst Delete( int i, List PtrL)
{
LIst p, s; // 分不清 struct LNode* 和 List
if( i ==1)
{
s = PtrL;
if( PtrL != NULL)
PtrL = s-> Next;
else
return NULL;
free(s);
return PtrL; //返回 PtrL 有神马用?
}
p = FindKth( i-1, PtrL);
if( p == NULL)
{
cout<<" 第 "<< i-1 <<" 个节点不存在!"<Next == NULL)
{
cout<<" 第" << i <<" 个节点不存在! "<Next;
p->Next = s->Next;
free(s);
return PtrL;
}
}
5、广义表:
例:
广义表是线性表的推广 :
线性表->元素都为单元素
广义表 -> 元素不仅可以是单元素,还可以是另一个广义表
定义创建:
typedef struct GNode &GList;
struct GNode
{
int Tag; // 标志域,0 表示节点是单元素,1 表示节点是广义表
union
{ //子表指针域SubLIst 与单元素数据域 Data 复用(公用存储空间)
ElementType Data;
GList SubList;
}URegion;
GList Next; //指向后继结点
};
6、多重链表
链表中的界定啊可能同时属于多个链:节点指针域会有多个(前例中 Next 和 SubLIst 两个指针域)。但含两个指针域的链表并不一定是多重链表 (双向链表)。树、图可采用多重链表
例:稀疏矩阵 学生选课
利用十字链表代替稀疏矩阵
例:多项式相加
采用不带头结点的单链表,按照指数递减的顺序排列
struct PolyNode{
int coef; // 系数
int expon; // 指数
struct PolyNode *link; // 指向下一个节点的指针
};
typedef struct PolyNode *Polynomial; // 结构体指针变量
Polynomial P1, P2; // 结构的指针
P1 P2 分别指向这两个多项式第一个节点(判断expon是否相等),不断循环
判断:
(1) P1->expon == P2->expon : P(新的一项,新的系数) = P1->coef + P2->coef -----> P1->link; P2->link(P1、P2指向下一项)
(2)P1->expon > P2->expon : P(新的一项,新的系数) = P1->coef -----> P1->link; (将P1的值存入当前多项式,并且P1 指向下一项)
(3)P1->expon < P2->expon : P(新的一项,新的系数) = P2->coef -----> P2->link;
接着:有一个多项式处理完时,比较结束,另一个多项式将没有比较晚的项接新的多项式之后
void Ayyach(int c. int e, Polynomial *pRear)
{ Polynomial P;
P = (Polynomial)malloc(sizezof(struct PolyNode)); // 给 指针P 计算存储空间
P->coef = c; // 将新的系数赋给P
P->expon = e; // 将新的指数赋给P
P->link = NULL; // P后为空
(*pRear)->link = P; // 将
*pRear = P; //
}
Polynomial PolyAdd ( Polynomial P1, Polynomial P2 )
{
/* 创建临时表头空节点,front、rear首先指向,front 指向表头节点,rear 指向链表的尾部, temp 用于最后释放空的表头,因为要返回新的多项式的头结点 */
Polynomial front, rear, temp;
int sum;
rear = (Polynomial) malloc (sizeof (struct PolyNode));
front = rear; // front rear 指向头,用front记录新多项式的头结点
while (P1 && P2) // 两个多项式都没有遍历完,即都不为空时
switch ( Compare(P1->expon, P2->expon))
{ case 1:
Attach (P1->coef, P1->expon, & rear);
P1 = P1->link;
break;
case -1:
Attach(P2->coef, P2->expon, & rear);
P2 = P2->link;
break;
case 0:
sum = P1->coef + P2->coef;
if( sum ) Attach( sum, P1->expon, &rear);
P1 = P1->link;
P2 = P2->link;
break;
}
// 将未处理完的,遗留下的项放在结果多项式中
for( ; P1; P1 = P1->link) Attach( P1->coef, P2->expon, &rear);
for( ; P2; P2 = P2->link) Attach( P2->coef, P2->expon, &rear);
rear->link = NULL;
temp = front;
front = front->link; // front 真正指向新多项式的有值的头结点
free(temp);
return front; // 返回新多项式的头指针,以便在其他函数结构体中调用
}