拜占庭将军问题(二)——口头协议
在上一篇文章中,介绍了拜占庭将军问题的描述、条件和结论。在传输口头消息(Oral Messages)时,少于3m+1个将军中有m个叛徒时,拜占庭将军问题是无解的。Leslie在原文1中, 提出了一种传输口头消息时拜占庭将军问题的一种解法。
定义
首先,为定义口头消息,拜占庭将军消息系统具有以下假设:
A1. 每个消息被正确发送。
A2. 消息的接收者知道是谁发送的消息
A3. 可以被检测到缺少消息
假设A1和A2防止叛徒干扰其他两个将军的通信,假设A3防止叛徒通过不发消息干扰一致性达成。
另外,口头协议算法要求每个将军可以与其他任意将军直接进行通信,Leslie在其原文中的第五章中描述了不需要满足这个条件的算法。
OM(m)算法
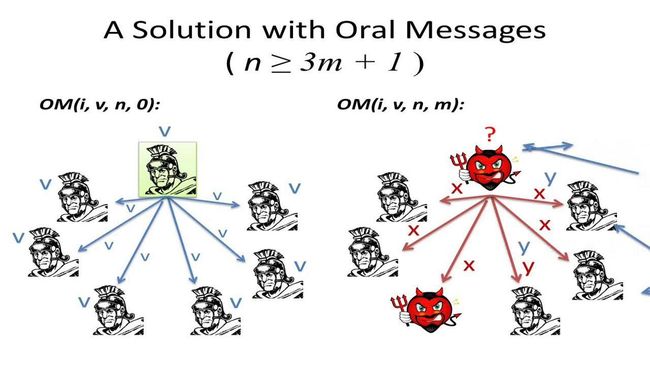
Leslie针对口头消息(Oral Messages)的情况,提出了口头协议算法***OM(m)***,其中m为非负。***OM(m)***算法是一个递归算法,用来处理在***3m+1***个将军中至多存在***m***个叛徒的情况。
默认行动:副官如果在指定时间内收不到来自司令的命令,则默认采取“撤退”行动。这是为了防止司令官为叛徒时,通过不发出命令来阻碍达成共识。
行动函数:算法假设使用***majority*方法作为行动函数,即当 v i v_i vi的大多数为v时,则 m a j o r i t y ( v 1 , . . . , v n − 1 ) = v majority(v_1, ..., v_{n-1})=v majority(v1,...,vn−1)=v
注:其实对于行动函数,有两种比较容易想到的选择:
- v i v_i vi的大多数值v,如果不存在大多数采取默认行动——“撤退”;
- 如果 v i v_i vi是个有序的集合,采用其中位数。
OM(m)算法:采用递归定义,下面分别说明**OM(0)和OM(m)**的内容。
当 m = 0 m=0 m=0时,
OM(0)算法
(1) 司令发送他的值给每个副官;
(2) 如果副官收到司令的值,使用这个值;否则,使用默认值——“撤退”。
当 m > 0 m>0 m>0时,
OM(m)算法
(1) 司令发送他的值给每个副官;
(2) 对于每个 i i i,令 v i v_i vi为副官 i i i从司令接收到的值;如果没有收到值,则 v i v_i vi采用默认值——“撤退”。在***OM(m-1)***算法中,副官 i i i作为司令向另外***n-2**个副官(不包括OM(m)*中的司令)发送值 v i v_i vi。
(3) 对于每个 i i i,对于每个 j ≠ i j\neq i j̸=i的 j j j,令 v i v_i vi为副官 i i i在第(2)步中从副官 j j j接收的值;如果没有接收到值,则使用默认值——“撤退”。副官 i i i用 m a j o r i t y ( v 1 , . . . , v n − 1 ) majority(v_1, ..., v_{n-1}) majority(v1,...,vn−1)作为其值。
举例:m=1, n=4
- 当一个副官是叛徒时
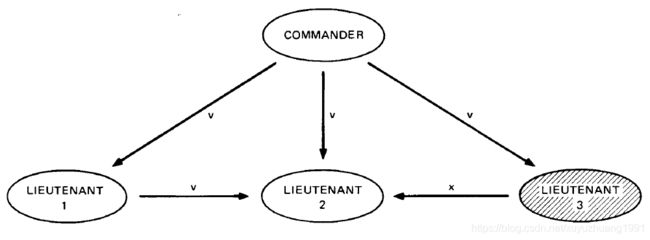
假设副官3是叛徒,下图针对副官2收到的消息对**OM(1)**进行阐述。
第一步:司令向每个副官发送他的值 v v v给每个副官;
第二步:副官1执行OM(0),作为司令向副官2发送 v v v;由于副官3是叛徒,其执行OM(0)向副官2发送了不同的值,假设为 x x x;
第三步:副官2拥有的行动值集为 { v 1 , v 2 , v 3 } = { v , v , x } \{v_1, v_2, v_3\}=\{v, v, x\} {v1,v2,v3}={v,v,x},采用majority**函数,副官2采取的行动值为 v = m a j o r i t y { v 1 , v 2 , v 3 } v=majority\{v_1, v_2, v_3\} v=majority{v1,v2,v3}。
同理,副官1采取的行动指令也是 v v v,即满足拜占庭将军问题一致性条件IC1和IC2。
注:拜占庭将军问题一致性条件为:
IC1. 所有忠诚副官遵守同一命令;
IC2. 如果司令官是忠诚的,每个忠诚的副官遵守他的命令。
- 当司令为叛徒时
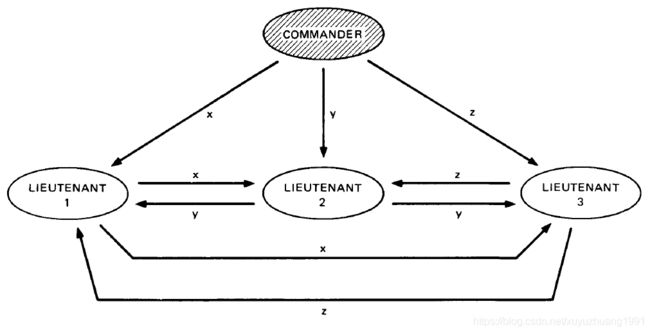
下图描述了当司令为叛徒,三位副官是忠诚的情况对**OM(1)**算法进行阐述。
第一步:司令为了阻止忠诚副官达成一致,分别向三位副官发送值 { x , y , z } \{x, y, z\} {x,y,z};
第二步:每个副官从司令收到的值作为自己的值,并执行OM(0)向其他副官发送;
第三步:在第三步中,每个副官拥有的值集均为 { x , y , z } \{x, y, z\} {x,y,z},因此,副官执行行动函数majority**得到的结果是一样的。
由于三位忠诚的将军采取同样的行动,满足拜占庭将军一致性条件IC1。
从m=1, n=4的例子可以看出,OM(m)算法能够处理拜占庭将军问题。在OM(m)算法中,独立执行了n-1次OM(m-1),且每个OM(m-1)算法独立执行了n-2次OM(m-2)……这就意味着,每个副官可能独立发送多轮消息。为了避免混淆,需要区分每轮消息。最易想到的方法是,每个副官 i i i在为第(2)步的值 v i v_i vi添加前缀 i i i。可以看出,算法**OM(m-k)**将被调用 ( n − 1 ) . . . ( n − k ) (n-1)...(n-k) (n−1)...(n−k)次,发送拥有 k k k个副官序号前缀的值。
**OM(m)**算法证明
本节采用归纳法证明**OM(m)**算法能够解决拜占庭将军问题。
引理
为了证明**OM(m)**算法,我们首先来证明一条引理:
对于任意的 m m m和 k k k,如果在多于 2 k + m 2k+m 2k+m个将军中至多存在 k k k个叛徒,则OM(m)算法满足条件IC2。
证明: 归纳法,针对参数 m m m进行归纳。
当 m = 0 m=0 m=0时,根据假设A1和**OM(0)**算法,易得如果司令是忠诚的,忠诚的将军按照司令的指令行动,引理是成立的。
当 m > 0 m>0 m>0时,假设在 m − 1 m-1 m−1时,引理成立,下面来证明在 m m m时,引理也成立。
在OM(m)的第一步,司令发送值 v v v给他的 n − 1 n-1 n−1个副官;
在第二步,每个忠诚的副官在 n − 1 n-1 n−1个副官中执行**OM(m-1)**算法。根据假设 n > 2 k + m n>2k+m n>2k+m,则 n − 1 > 2 k + ( m − 1 ) n-1>2k+(m-1) n−1>2k+(m−1),所以根据引理在 m − 1 m-1 m−1时成立,可得,每个忠诚的将军从忠诚的将军 j j j处获得的值为 v j = v v_j=v vj=v。
在第三步中,由于叛徒最多有 k k k个,且 n − 1 > 2 k + ( m − 1 ) ≥ 2 k n-1>2k+(m-1)\geq 2k n−1>2k+(m−1)≥2k,所以 n − 1 n-1 n−1个将军中的忠诚将军为大多数。所以第三步每个忠诚的将军获得值 m a j o r i t y ( v 1 , . . . , v n − 1 ) = v majority(v_1, ..., v_{n-1})=v majority(v1,...,vn−1)=v,满足条件IC2。
引理得证。
证明
下面来证明算法**OM(m)**能够解决拜占庭将军问题。
定理 1:对于任意 m m m,如果存在多于 3 m 3m 3m个将军中至多有 m m m个叛徒时,OM(m)算法满足条件IC1和IC2。
证明:针对变量 m m m采用归纳法。
当 m = 0 m=0 m=0时,即没有叛徒存在,则很容易证明OM(0)满足条件IC1和IC2。
假设在 m − 1 m-1 m−1时,定理成立,下面证明在 m m m时,定理也成立。
- 当司令是忠诚的
令引理 1中的 k = m k=m k=m,即多于 3 m 3m 3m个将军中至多存在 m m m个将军时,OM(m)满足条件IC2。又因为当司令是忠诚的时,条件IC1包含在条件IC2中,所以OM(m)也满足条件IC1。
- 当司令是叛徒时
由于至多有 m m m个叛徒,所以至多存在 m − 1 m-1 m−1个副官是叛徒。因为将军的数量多于 3 m 3m 3m,所以副官的数量也多于 3 m − 1 3m-1 3m−1,且 3 m − 1 > 3 ( m − 1 ) 3m-1>3(m-1) 3m−1>3(m−1)。根据递归假设算法OM(m-1)满足条件IC1和IC2,所以在第三步,对于每个副官 j j j,任意两个忠诚的副官得到相同的 v j v_j vj。(如果副官 j j j是两个中的一个,运用条件IC2;否则,运用条件IC1)。
所以,任意两个忠诚的副官能获得相同的指令值集 { v 1 , . . . , v n − 1 } \{v_1, ..., v_{n-1}\} {v1,...,vn−1},因此,在OM(m)的第三步中,忠诚将军遵从相同的值,即 m a j o r i t y ( v 1 , . . . , v n − 1 ) majority(v_1, ..., v_{n-1}) majority(v1,...,vn−1)。所以,算法OM(m)满足条件IC1。
综上所述,定理 1得证。
小结
本文介绍了在将军之间直接传送口头消息(Oral Messages)时,解决拜占庭将军问题的算法OM(m),并对其在 m = 1 m=1 m=1且 n = 4 n=4 n=4时进行了举例说明,最后对**OM(m)**算法进行了证明。
接下来的文章中,将对将军之间传输签名的书面消息(Signed Messages)时,解决拜占庭将军问题的算法进行阐述。
Lamport L, Shostak R, Pease M. The Byzantine generals problem[J]. ACM Transactions on Programming Languages and Systems (TOPLAS), 1982, 4(3): 382-401. ↩︎