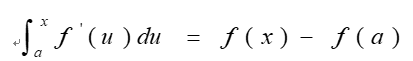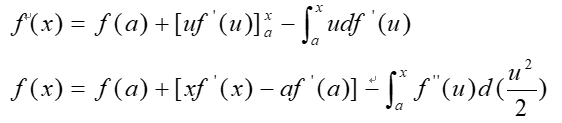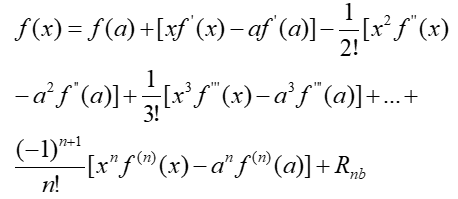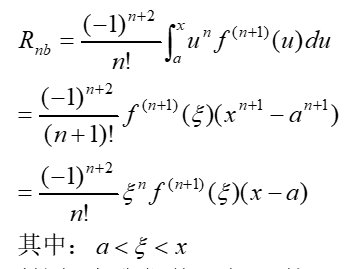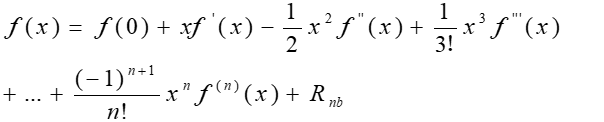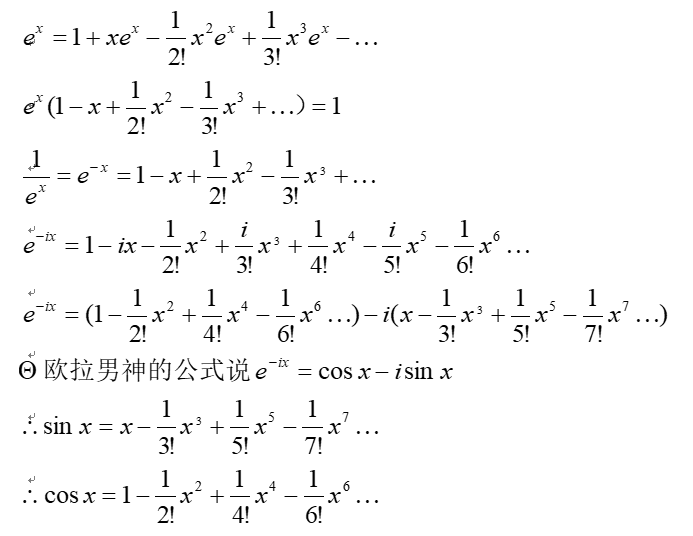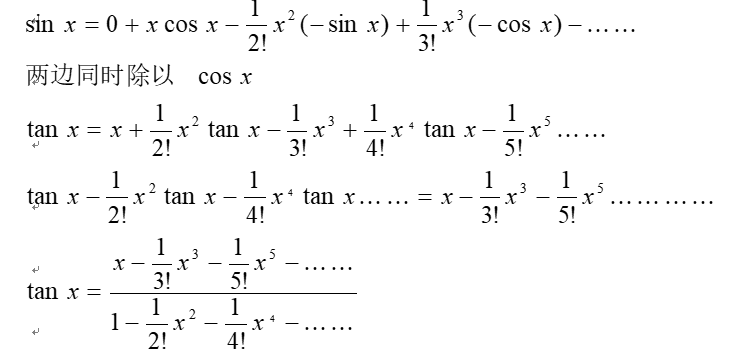泰勒公式与函数展开的操作方法

01

说在前面的话

传说早在亚里士多德时代（相当于我国的战国），就有人在探寻将一般函数展开成简单多项式的方法，但因为条件所限，一直未能成功。不过在漫长的历史长河中，在具体数值求解方面仍有很多经典实例让后世的我们眼前一亮，比如古人制定十二平均律规范了音律。另外，通过割圆术计算圆周率更可以认为是近似计算的经典范例。古人在长期观测中注意到天体运行轨道速率与加速度变化产生的视运动变化，在天文历算（主要是编订历法）过程中引入了内插法。东汉时，刘洪编订《乾象历》引入一次内插。隋朝刘焯编订《皇极历》引入二次内插。唐代僧一行（俗名张遂）编订《大衍历》时，修正了刘焯的方法。元代郭守敬、王恂在编订《授时历》过程中引入了三次内插，辅以差分表计算，并将此法命名为“招差”（南宋秦九韶称之为“招法”），即“招差术”之由来。元朝的朱世杰在《四元玉鉴》中，讨论了更一般情况下的“招差法”。

从《九章算术》盈不足术的直线内插法历经东汉刘洪、隋刘焯、唐一行与徐昂, 到元郭守敬与朱世杰的四次招差术, 实质上已到达了牛顿的一般插值公式,此时实际上距离泰勒展开式已只一步之遥。

300多年后的1712年（相当于中国清朝康熙51年），传说牛顿的门生英国人泰勒（Brook.Taylor），找到了一个方法，成功将函数展开为多项式。下面，我们探讨从微积分基本公式（牛顿－莱布尼茨公式）出发，通过运用分部积分法把函数展开。因为是科普文所以这里不做严格的推导、论证，且遣词用句可能有乡间哩语。鉴于此文俗不可耐的文风，可能须要您在摇头叹息中才能读完全文。但还是希望既使您已完全忘了微积分的内容也可从这篇科普文里有所收获！

02

函数的展开式

根据微积分基本公式：

 

这个∫符号就大名鼎鼎的积分号啦，她其实是个拉长的S，是著名的莱布尼茨大神在与牛顿大叔骂战前就开始使用的，在她右上侧的x叫做积分上限，她下面的a自然就名叫下限啦（因为人家是s形身材所以称“她”，有任何人不服气吗？），当然如果你感觉她旁站这两个字母不够帅气的话也可以换另外两个，随便你！接下来的ƒ代表一个函数（相信你仍然记得），这个右上面的小撇就代表导函数了（简称导数），u代表自变量（不喜欢的话你也可以换成t、l、v、w、z，总之你随意），后面我看到了d这个字母是代表微分符号。等号的右边是这个函数在x点对应的值减去她在a点的值。啊！遥想300多年前两大终身未娶的男神那一场惊天地泣鬼神的骂战，难道是为了“她”……

收摄心神，长话短说，上面的式子说的是：一个函数先微分后积分就等于这个函数本身在积分上限点的值减去她在下限点的值。什么？这不就是说S姐姐脱了外套又穿上了外套，多费手续。不就是要称下人家的体重吗？搞的这么迂回！其实很多看起来高大上的数理化公式、定理用普通人话表达都是很平易近人的。所以就有（1）式：

运用分部积分法，什么？分部积分法也记不得啦！好吧我点下：

d(uv)= udv+vdu所以∫udv=uv-∫vdu

不费解释啦啦，那么就有（2）式：

继续使用分部积分法，有（3）式：

以此类推，有（4）式：

余项Rnb根据积分中值定理可以写成下面的样子（什么？你想知道为什么Rn后面比书上多了个B，那我告诉你是为了和教科书上的方法有所区别。如果你非要刨根问底为么用B这个字母？那俺告诉你，那是俺的笔名的首字母，你要是不服去掉俺也没办法打到你。你要心烦的话大可以不看这个部分）：

通过上面的努力我们终于把函数展开了，只是好像有点丑。好吧，让我们放个大招！当a=0时：

是不是好看了许多，下面我们利用这个成果，举两个例子，利见大人、利涉大川、利有攸往、利贞的展开常用函数：

当然我们也可以像下面这样，胡搞一下扫堂腿法：

你想得到其它函数的展开式可以继续试，如果是求其她三角函数的话也可以直接用暴力三角万能公式。具体的不多说了，考虑自行脑洞，啦啦！

03

经过上面一轮操作，如果你还是心心念念，不忘泰勒公式，那么就可以这样

有人一定想说，为什么会比文前最开始式子的du凭空多减了一个x，想骗过我的火眼睛睛！其实这就是微积分中的基本原理了，你可以在d后面的u上加减任意“常量”，当然你也可以减去a试试。有人说为什么不加上或减去其她的数呢？因为我们的目的是精简计算过程，而不是旁生支节，使她更加烦人，不信你试试！

3.1  由上式运用分部积分法可得到（5）式：

 

需要注意一下，（a-x)=-(x-a),她们的奇次方有相同的表现。但她们的平方、四次方等偶次方确相等，而并不随着a和x位置转换而变换为负值。那么，继续运用分部积分法有（6）式：

这就是这就是让你心心念念的泰勒公式啦！

04

写在后面的话

在我们学习泰勒公式的时侯，大多都很想知道乍样能得到这个公式，但遗憾的是，教科书和绝大多数的学习资料只侧重于证明定理本身，多数情况下，还必须先要预设一些条件并找到XXX，然后又要证明它与XX同阶等等。而对初学者（尤其是学渣）来说这些过程非但不是很自然和容易接受，简直就是要人老命的老辣文风。我们的这篇骚文就非常亲民和低调，所述的方法尽量减少了推理论证这些方法和过程的支撑，希望可以有助于学已渐忘的您回想起300年前旷世大神们的神来大作乃至微积分的主要内容。另外提下醒，看明白了这篇通俗体文字不代表您已学懂了泰勒公式和微积分，还是要会做教课书上的习题才成哦！！

参考文献：

［1］   同济大学应用数学系. 高等数学. 北京：高等教育出版社，1997.242-263

［2］   吴文俊.中国古代数学对世界文化的伟大贡献.数学学报.1975年第18卷第1期

［3］   李轻舟.两则有趣的科学史：岁星纪年与招差术.科学网博客

编辑 ∑Gemini

来源：数学算法俱乐部

文章推荐

☞数学家探索两个几何世界之间的镜像链接

☞数学天才帕吉特：他有如电影般的人生际遇

☞世界上最奇怪的数学天才，被奖励100万却拒领，宁愿过得像乞丐

☞斯坦福大学教育学院院长：学习本身就是一门学问

☞如果没有数学，我们如何测量

☞数学的真相：物理时空的数字模型还是现实本身？