PBFT算法简介
一、顾名思义
PBFT(Practical Byzantine Fault Tolerance)算法,是一个能够容忍拜占庭错误的分布式系统共识算法。
首先这里需要解释上面几个名词:
拜占庭错误:
所谓拜占庭错误,通俗来讲,可以理解成人为的故意作恶导致的错误,相对于普通的宕机错误,拜占庭错误是一种有目的的作恶行为。之所以叫拜占庭错误,是因为这类共识一开始是要解决Leslie Lamport提出的“拜占庭将军问题”。
所谓的拜占庭将军问题,就是一组拜占庭将军约定分兵共同攻打一座城池,在是否发起总攻的问题上,拜占庭将军之间需要通过信使交换消息来得到最后的决定,当且仅当大部分将军得到相同的结果(攻打或者撤退),才不会导致因为兵力不足攻打城池失败。由于叛徒的存在,将军可能会故意散布虚假消息,伪造消息等方式影响其他将军的最终决策。这个共识问题也就是拜占庭将军问题,而拜占庭错误则是指在分布式系统中,节点可以通过制造各种错误来影响其他节点的共识。
分布式系统与共识:
分布式系统是指该系统是由多个点对点的地位平等的节点组成系统,整个系统对外表现成一个单一的系统,因此需要在节点和节点之间对系统的状态形成一致性结果,即所谓的共识。
二、条分缕析
PBFT到底解决了什么问题?
简单来说,PBFT只是解决了一个系统对系统操作的排序问题。我们知道,系统的当前的状态 = 初始状态 + 一些列有序状态数据操作。将数据操作看做是一笔交易,则PBFT就是解决在一个可能出现拜占庭错误的分布式节点中如何对交易的顺序达成共识的问题。
PBFT是怎么做的?
PBFT将交易的排序问题分解成三部分,一部分是交易的提出(Proposal),一部分是交易的投票,一部分是交易的提交(Commit)。所谓commit,即是将该笔交易放在一个特定的顺位执行。
PBFT要达到的效果是:在拜占庭节点(可能出现拜占庭错误的节点) 数量不超过1/3的条件下,系统中非拜占庭节点之间的状态是一致的。
PBFT的思路是,只要保证每一个Proposal都是唯一且有序的&每一笔被commit的交易都对应一个Proposal&每一个被commit的交易都会被超2/3的节点commit。
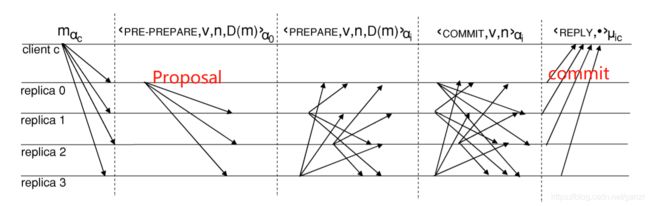
上图是PBFT算法流程图,结合图形说明PBFT是如何完成上面所说的三个目标:
1. “每一个Proposal都是唯一且有序的”
要实现这个效果非常简单,只要给每一个proposal赋值一个序号n,同时每一个非拜占庭节点约定不接受两个具有相同的n值的Proposal。因此,对于非拜占庭节点而言,每一个被接收的Proposal都是唯一且有序的。
2. “每一笔被commit的交易都对应一个Proposal”
PBFT算法流程可以看做由无数的轮次组成,在每一轮中,有一个Proposal被提出,节点通过“少数服从多数”原则决定一个Proposal是否被commit。即,每一个被commit的交易,首先是一个Proposal。
3. “每一个被commit的交易都会被超2/3的节点commit”
非拜占庭节点如何在一个靠消息通信的分布式节点网络中保证自己commit的交易会被超过2/3的节点commit?可以继续把这个条件拆分成两个:1)确定一个Proposal被超过2/3得节点投票;2)确定超过2/3的节点都确认了条件1)。
之所以需要同时满足条件1)和2),是因为在一个存在拜占庭节点网络中,节点自己接收到的消息和其他节点接收到的消息不一定是完全一样的,原因是拜占庭节点可能会传播虚假伪造的消息,即从每一个节点看到的“视图”(view)不一定是一样的。
PBFT是如何保证条件1)和2)?
1)在PBFT中,节点的通信消息使用非对称加密来保证真实性。所谓非对称加密,即对于一个原文,用密钥A加密之后,只能用一个不同的密钥B解密,反之亦然。因此,只要每一个节点都有一个公开的密钥(公钥),以及一个私密的密钥(私钥),并使用私钥来加密自己需要传输的消息,就可以使得其他节点使用这个节点的公钥来解密得到真实的消息。对于任意一个Proposal的投票信息,节点需要收集所有其他节点的投票信息,即图中PREPARE标注的部分——每一个节点都会将自己的投票消息广播以便其他节点收集。只要节点收集到超过2/3个节点的投票消息,就可以保证在本地节点的视图中,序列号n对应的就是被投票的Proposal。
简单证明如下:假设系统中的节点总数为3f+1,系统中至多有f个拜占庭节点,节点A和B都接收到了关于(n,Proposal),(n,Proposal1)的超过2/3,即存在至少2f+1个节点投票了(n,Proposal)以及至少2f+1个节点至少投票了(n,Proposal1)。因为节点总数为3f+1,因为至少存在2f+1+2f+1-3f-1=f+1个节点既投了(n,Proposal)又投了(n,Proposal),即所谓的拜占庭节点,与假设矛盾,因此,不会出现同一个序列化n,不同的Proposal会同时被超过2/3的节点投票。
可以看到,只要满足条件1),有且仅有一个唯一的(n,Proposal)会被超过2/3的节点投票。
2)条件1)对于一个节点而言,只是本地看到的视图,为了保证本地视图也是全局视图,节点需要将在条件1被满足之后,通过广播通知所有其他节点,当一个节点接收到超过2/3的节点发送了针对同一个(n,Proposal)条件1)被满足的通知,即可确定超过2/3的节点的视图和本地视图一致。即条件2)被满足。
当然,上述的算法流程只是保证了算法的安全性(safety),即,对于非拜占庭节点而言,最终commit的Proposal的顺序一定是一致的。但是没有保证算法的活性(liveness)。
所谓活性,是指整个系统在持续不断地形成共识。
活性的关键在于提出Proposal的节点是否为非拜占庭节点,如果是,则通过上述算法流程,最终该Proposal会被commit,如果提出Proposal的节点是拜占庭节点,则可能非拜占庭节点之间收到的Proposal都是不一致的,当然就不可能达成条件1)。
要解决算法的活性问题,一个可行的方案是超时机制,因为无法实现知道哪个节点是非拜占庭节点,所以如果非拜占庭节点发现当前负责提出Proposal的节点迟迟不能提出有效的Proposal,就会触发超时机制处理,从而挑选一个新的节点负责提出Proposal(Leader节点)。
挑选新的Leader节点,本质上也是一次共识,原则上需要首先提出一个Proposal来指定一个节点当选,然后经过上述的共识流程来commit这个Proposal从而实现Leader的选举。然而这样是行不通的,因为需要挑选Leader的原因就是现在Proposal无法正常被提出。因此,Leader的更换不能由Proposal发起,而是应该按照一个约定规则来确定下一个当选Leader的节点,当当前leader节点变成拜占庭节点后,所有其他节点会发送一个超时的投票给下一个应该当选leader的节点,而该节点在接收到超过2/3节点的投票时,正式成为了新的leader。这个过程也就是PBFT中所谓的view-change。
三、寻根问底
来复盘一下PBFT算法,整体上来看,整个算法是分为三个阶段,即,Proposal的提出,Proposal的投票,Proposal的提交。每一个阶段都可以达到一个具体的条件和目标,而三个条件和目标的达成之后,即可保证算法的安全性。将算法拆解成上述的三个阶段解决了系统共识的安全性问题,但是同时也引入了一个算法活性问题,即仅仅依靠上述的三个阶段的拆分是无法使得整个分布式系统持续的共识。PBFT的做法是将活性的解决用共识本身来解决,即所谓的view-change阶段来保证能够在有限的时间内挑选一个非拜占庭节点来当选leader,从而保证了上述阶段的第一个——Proposal的提出。
本质上来说,PBFT就是一个使用“少数服从多数”原则来达成共识的算法。但是同时PBFT做了关键的基础同步——包括节点的总数量,节点的视图值(视图值是挑选leader节点规则算法的输入值,只要视图值一致,输出的当选leader就一致),视图超时时间等等。在理解PBFT算法的时候,需要结合算法的假设前提以及算法的规则本身。书不尽言,有兴趣的同学可以继续研究一下PBFT算法原文。笔者个人觉得Lamport的论文用词精准,逻辑缜密,值得好好探索。