清华学霸总结的动态规划4步曲,仅这篇动归够了
本文作者:
九章算法《动态规划专题》金牌讲师
清华大学全国算法竞赛金牌,ACM国际大学生程序设计竞赛全球总决赛选手。FLAG资深面试官。
动态规划题目类型多,难度高,没有固定模板,死记硬背没用。
作为大厂高频面试题,动态规划问题的识别与解决一直是难点所在,往往也是决定面试成功与否的最终关卡。
不过不用怕,我总结了解决动态规划类问题的4步套路,分享给大家。
先备一份见面礼——7.2个G的5月最新大厂求职资料,感兴趣的同学可以长按识别白嫖~望笑纳
侯卫东的见面礼
FLAG高频动态规划66题
国内外大厂最新算法面试题
一线互联网公司真题解析
2020大厂面经汇总
礼包部分内容,长按扫码即可领取
4步套路,解决动态规划问题
1、确定问题状态
- 提炼最后一步
- 子问题转化
2、转移方程,把问题方程化
3、按照实际逻辑设置初始条件和边界情况
4、确定计算顺序并求解
结合实例感受下。
你有三种硬币,分别面值2元,5元和7元,每种硬币都有足够多。买一本书需要27元。如何用最少的硬币组合正好付清,不需要对方找钱?
关键词“用最小的硬币组合正好付清”——“最小的组合”,求最值问题,动态规划。
正常人第一反应思路:
最少硬币组合?
优先使用大面值硬币——7+7+7+5=26 额?可求解目标是27啊……
改算法——7+7+7+2+2+2=27,总共用了6枚硬币正好27元.
实际正确答案:7+5+5+5+5=27,才用了5枚硬币。
所以这里贪心算法是不正确的。
套路用起来。
第一步,确定问题状态。
动态规划问题求解需要先开一个数组,并确定数组的每个元素f[i]代表什么,就是确定这个问题的状态。
类似于解数学题中,设定X,Y,Z代表什么。
A、确定状态首先提取【最后一步】
最优策略必定是K枚硬币a1, a2,…, aK 面值加起来是27。
找出不影响最优策略的最后一个独立角色,这道问题中,那枚最后的硬币“aK”就是最后一步。
把aK提取出来,硬币aK之前的所有硬币面值加总是27- aK
因为总体求最硬币数量最小策略,所以拼出27- aK 的硬币数也一定最少(重要设定)。
B、转化子问题。
最后一步aK提出来之后,我们只要求出“最少用多少枚硬币可以拼出27- aK”就可以了。
这种与原问题内核一致,但是规模变小的问题,叫做子问题。
为简化定义,我们设状态f(X)=最少用多少枚硬币拼出总面值X。
我们目前还不知道最后的硬币aK面额多少,但它的面额一定只可能是2/5/7之一。
如果aK是2,f(27)应该是f(27-2) + 1 (加上最后这一枚面值2的硬币)
如果aK是5,f(27)应该是f(27-5) + 1 (加上最后这一枚面值5的硬币)
如果aK是7,f(27)应该是f(27-7) + 1 (加上最后这一枚面值7的硬币)
除此以外,没有其他的可能了。
至此,通过找到原问题最后一步,并将其转化为子问题。
为求面值总额27的最小的硬币组合数的状态就形成了,用以下函数表示:
f(27) = min{f(27-2)+1, f(27-5)+1, f(27-7)+1}
第二步,转移方程,把问题方程化。
f[X] = min{f[X-2]+1, f[X-5]+1, f[X-7]+1}
(动态规划都是要开数组,所以这里改用方括号表示)
实际面试中求解动态规划类问题,正确列出转移方程正确基本上就解决一半了。
但是请问:这与递归有什么不同??
递归的解法:
// f(X)返回最少用多少枚硬币拼出X int f(int X) { // 0元钱只要0枚硬币 if (X == 0) return 0; // 初始化用无穷大(为什么是正无穷?) int res = MAX_VALUE; // 最后一枚硬币是2元 if (X >= 2) { res = Math.min(f(X – 2) + 1, res); } // 最后一枚硬币是5元 if (X >= 5) { res = Math.min(f(X – 5) + 1, res); } // 最后一枚硬币是7元 if (X >= 7) { res = Math.min(f(X – 7) + 1, res); } return res;}
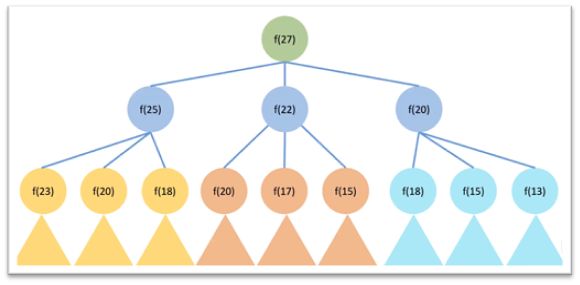
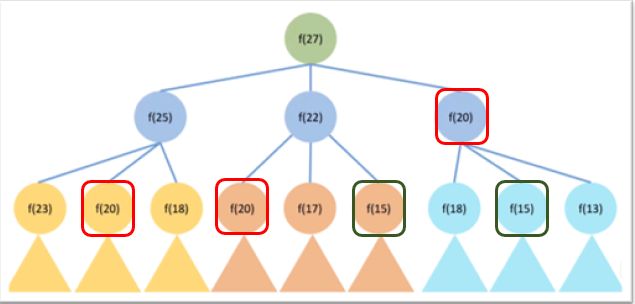
执行图如下:
要算f(27),就要递归f(25)、f(22)、f(20),然后下边依次递归……(三角形表示)。
问题明显——重复递归太多。
这是求f(27),还可以勉强递归。如果求f(100)呢?简直是天文数字。最终结果就是递归超时。
求总体最值,一定优先考虑动态规划
不要憨憨的去递归。
插入一下~
需要掌握的动态规划面试解题技巧还包括坐标型、位操型、序列型、博弈型、背包型、双序列以及一些高难面试题解。
本文篇幅有限无法逐一讲清,大家来白嫖我的在线分享吧(纯干货)。
白嫖方式:
长按扫码 — 跳转页面左下 —【免费试听】按钮即可????
或点击最下方“阅读原文”
第三步,按照实际逻辑设置边界情况和初始条件。
【必做】否则即使转移方程正确也大概率无法跑通代码。
f[X] = min{f[X-2]+1, f[X-5]+1, f[X-7]+1}的边界情况是[x-2]/[x-5]/[x-7]不能小于0(硬币面值为正),也不能高于27。
故对边界情况设定如下:
如果硬币面值不能组合出Y,就定义f[Y]=正无穷
例如f[-1]=f[-2]=…=正无穷;
f[1] =min{f[-1]+1, f[-4]+1,f[-6]+1}=正无穷,
特殊情况:本题的F[0]对应的情况为F[-2]、F[-5]、F[-7],按照上文的边界情况设定结果是正无穷。
但是实际上F[0]的结果是存在的(即使用0个硬币的情况下),F[0]=0。
可是按照我们刚刚的设定,F[0]=F[0-2]+1= F[-2]+1=正无穷。
岂不是矛盾?
这种用转移方程无法计算,但是又实际存在的情况,就必须通过手动定义。
这里手动强制定义初始条件为:F[0]=0.
而从0之后的数值是没矛盾的,比如F[1]= F[1-2]+1= F[-1]+1=正无穷(正无穷加任何数结果还是正无穷);F[2]= F[2-2]+1= F[0]+1=1……
第四步,确定计算顺序并计算求解
那么开始计算时,是从F[1]、F[2]开始呢?还是从F[27]、F[26]开始呢?
判断计算顺序正确与否的原则是:
当我们要计算F[X](等式左边,如F[10])的时候,等式右边(f[X-2], f[X-5], f[X-7]等)都是已经得到结果的状态,这个计算顺序就是OK的。
实际就是从小到大的计算方式(偶有例外的情况我们后边再讲)。
例如我们算到F[12]的时候,发现F[11]、F[10]、F[9]都已经算过了,这种算法就是对的;
而开始算F[27]的时候,发现F[26]还没有算,这样的顺序就是错的。
很显然这样的情况下写一个FOR循环就够了。
回到这道题,采用动态规划的算法,每一步只尝试三种硬币,一共进行了27步。算法时间复杂度(即需要进行的步数)为27*3。
与递归相比,没有任何重复计算。
原题练习及实际代码:
这道题是lintcode编号669的Coin Change问题。
代码如下:
public int coinChange(int[] A, int M){ // A = [2,5,7] // M = 27 int[] f = new int[M + 1]; int n = A.length; // 硬币的种类
// 初始化, 0个硬币 f[0] = 0; // f[1], f[2], ... , f[27] = Integer.MAX_VALUE for (int i = 1; i <= M; i++){ f[i] = Integer.MAX_VALUE; } for (int i = 1; i <= M; i++){ // 使用第j个硬币 A[j] // f[i] = min{f[i-A[0]]+1, ... , f[i-A[n-1]]+1} for (int j = 0; j < n; ++j){ // 如果通过放这个硬币能够达到重量i if (i >= A[j] && f[i - A[j]] != Integer.MAX_VALUE) { // 获得i的重量的硬币数就可能是获得i-A[j]重量硬币数的方案+1 // 拿这个方案数量与原本的方案数打擂台,取最小值就行 f[i] = Math.min(f[i - A[j]] + 1, f[i]); } } }
if (f[M] == Integer.MAX_VALUE){ return -1; } return f[M];
}
最后总结:
![]()
1、这是求最值问题,用动态规划方式求解。
2、进入求解过程,先确定问题状态
- 提炼最后一步
(最优策略中使用的最后一枚硬币aK)
-子问题转化
(最少的硬币拼出更小的面值27-aK)
3、构建转移方程
f[X] = min{f[X-2]+1, f[X-5]+1, f[X-7]+1}
(求min是因为题目要求求最小)
4、设置初始条件和边界情况
f[0] = 0, 如果不能拼出Y,f[Y]=正无穷
5、确定计算顺序并计算求解
f[0], f[1], f[2]……
![]()
实际上按照以上4步套路,基本上可以应对绝对大多数的动态规划面试题。
动态规划专题班 免费分享课
限时白嫖
长按扫码,点击免费报名即可
或点击下方“阅读原文”
![]()
白嫖戳这里