一元以及二元多项式插值拟合(泰勒)
申明: 仅个人小记
根本上是基于泰勒公式,包括一元的和二元的泰勒定理。 泰勒用多项式逼近的思想。
效果展示
一元
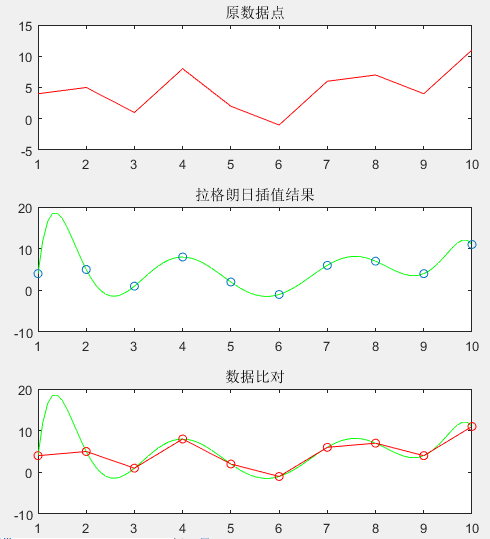
二元
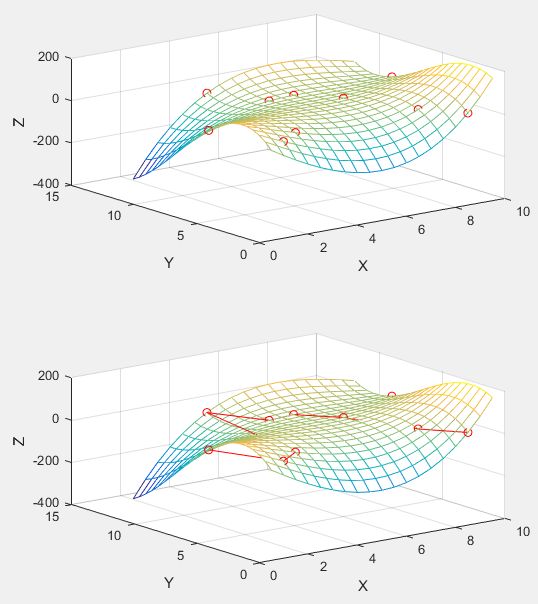
原理交代
一元

二元
Matlab代码
一元
% 本质上就是n个方程解n个未知数,这里的未知数是待求函数的所有系数
% Ac=Y A是由X组成的范德蒙德行列式,根据范德蒙德行列式的性质,
%为保证可解,X中不允许出重复的数值
X = 1:10;
Y = [4,5,1,8,2,-1,6,7,4,11];
% 很有意思,用到了范德蒙德行列式
% 因为范德蒙德行列式有很好的技巧性的计算方法,所以可能提供更好的计算方法
% 因为是范德蒙德行列式,所以,很容易知道什么情况该行列式不为零
n = length(X);
A = ones(n,n);
for j = 2:n % 从第二列开始,根据X计算相应的范德蒙德矩阵
for i = 1:n
A(i,j) = X(i)*A(i,j-1);
end
end
c = inv(A)*Y'; % 得到系数c, 即得到了相应的拟合函数
% f(x) = c0+c1*x+c2*x^2+...+cn-1 * x^(n-1)
% 下面绘出拟合函数
x = min(X):0.1:max(X); %
y = zeros(1,length(x));
for i = 1:length(x) % 带入x 计算 y
t = 1;
for j = 1:n
y(i) = y(i)+t*c(j);
t = t * x(i);
end
end
subplot(311)
plot(X,Y,'r')
title('原数据点')
subplot(312)
plot(x,y,'g')
hold on
plot(X,Y,'O')
title('拉格朗日插值结果')
hold off
subplot(313)
plot(x,y,'g')
hold on
plot(X,Y,'r')
plot(X,Y,'ro')
title('数据比对')
hold off
二元
close all
clear all
X = [1 2 3 4 5 6 7 8 9 10]
Y = [6 2 3 12 9 9 7 3 1 9];
Z = [3 2 5 6 3 9 11 9 8 12];
n = length(X); % 必须保证 n = 1+2+3+...+m, m为整数
m = floor(sqrt(2*n))-1; % 计算相应目标函数的阶数, 从 0 阶开始
%% 数据计算准备
% tt 中的内容及意义
% 0 阶 1阶 2阶 3阶
% x的次幂 0 , 0 1 , 0 1 2 , 0 1 2 3 , ...
% y的次幂 0 , 1 0 . 2 1 0 , 3 2 1 0 , ...
tt = zeros(2,n);
k = 1;
for i = 0:m
for j = 0:i
tt(1,k) = j;
tt(2,k) = i-j;
k = k+1;
end
end
%% 根据tt, X, Y, 计算相应的系数矩阵 A
A = ones(m,m);
for i = 1:n
k = 1;
for j = 1:n
A(i,j) = power(X(i),tt(1,k))*power(Y(i),tt(2,k));
k = k+1;
end
end
c = inv(A)*Z'; % 得到目标函数的系数, 即得到 z = f(x,y)
%% 绘制目标拟合函数图
% z = f(x,y)
[x, y] = meshgrid(min(X):0.5:max(X),min(Y):0.5:max(Y));
% 计算z值
z = zeros(size(x,1),size(x,2)); % 只是赋予z和x同样的规格
for i = 1:size(x,1)
for j = 1:size(x,2)
for k = 1:n
z(i,j) = z(i,j) + c(k)*power(x(i,j),tt(1,k))*power(y(i,j),tt(2,k));
end
end
end
subplot(211)
mesh(x,y,z)
xlabel('X')
ylabel('Y')
zlabel('Z')
hold on
plot3(X,Y,Z,'ro')
hold off
subplot(212)
mesh(x,y,z)
xlabel('X')
ylabel('Y')
zlabel('Z')
hold on
plot3(X,Y,Z,'ro')
plot3(X,Y,Z,'r')
2018年1月24日 13:41:16 Written by Jack Lu
