2019智能算法大赛总结（基于用户购买记录的二分类预测）

一、比赛说明：
评分标准
评分算法通过logarithmic loss（记为logloss）评估模型效果，logloss越小越好。
目标：预估用户人群在 规定时间内产生购买行为的概率 1买， 0不买

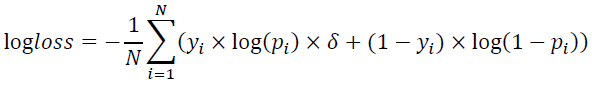
其中N 表示测试集样本数量，
yi 表示测试集中 第i个样本的真实标签，
pi 表示第 i个样本的预估转化率，
δ 为惩罚系数。
AB榜的划分方式和比例：
【1】评分采用AB榜形式。排行榜显示A榜成绩，竞赛结束后2小时切换成B榜单。B榜成绩以选定的两次提交或者默认的最后两次提交的最高分为准，最终比赛成绩以B榜单为准。

【2】此题目的AB榜数据采用 同时段数据 是随机划分，A榜为随机抽样测试集50%数据，B榜为其余50%的数据。

二、 数据集
https://pan.baidu.com/s/1cPX5jPCuOLDWkEGtCg6OcQ
提取码：uqb5
三、过程：

• 赛题分析
• 数据去操
• 特征选择、构造：挑选有用的特征，生成一些间接的特征（https://zhuanlan.zhihu.com/p/32749489）
• 模型选择
• 结果评估
  四、特征处理
  我们总共构建了75个指标，其中包括52个基本指标，23个重要指标的变换，平方，对数

购买次数: customer_counts

省份: customer_province

城市: customer_city

…
首先对其中的异常值进行处理，包括用众数填充，平均数填充。
之后对数据中的噪声（特殊值）进行处理，删除，改为指定数值，进而缩小数据的范围。
之后对范围较大的数据，做离差标准化处理，映射到（0，1）区间内。

# 此处只是列举了特征选取的一部分
for idx, data in enumerate([train_last, train_all]):
        customer_all = pd.DataFrame(data[['customer_id']]).drop_duplicates(['customer_id']).dropna()
        data = data.sort_values(by=['customer_id', 'order_pay_time'])
        data['count'] = 1
        # 一、购买次数
        tmp = data.groupby(['customer_id'])['count'].agg({'customer_counts': 'count'}).reset_index()
        customer_all = customer_all.merge(tmp, on=['customer_id'], how='left')
        # 二、 省份 , last() 由迭代式获取其中的值， reset_index() 重置索引
        tmp = data.groupby(['customer_id'])['customer_province'].last().reset_index()
        customer_all = customer_all.merge(tmp, on=['customer_id'], how='left')
        # 三、城市
        tmp = data.groupby(['customer_id'])['customer_city'].last().reset_index()
        customer_all = customer_all.merge(tmp, on=['customer_id'], how='left')
        # 四、long_time ： 在train 训练集中的 last - first 的时长, order_pay_date_last : 统计这个用户的订单最后一次购买时间
        last_time = data.groupby(['customer_id'], as_index=False)['order_pay_time'].agg(
            {'order_pay_date_last': 'max', 'order_pay_date_first': 'min'}).reset_index()
        tmp['long_time'] = pd.to_datetime(last_time['order_pay_date_last']) - pd.to_datetime(last_time['order_pay_date_first'])
        tmp['long_time'] = tmp['long_time'].dt.days + 1
        del tmp['customer_city']
        customer_all = customer_all.merge(tmp, on=['customer_id'], how='left')

解决倾斜特征

    # 解决倾斜特征
    numeric_dtypes = ['int16', 'int32', 'int64', 'float16', 'float32', 'float64']
    numeric = []
    for i in last.columns:
        if last[i].dtype in numeric_dtypes:
            numeric.append(i)

为所有特征绘制箱型线图

    import seaborn as sns
    import matplotlib.pyplot as plt
    sns.set_style('white')
    f, ax = plt.subplots(figsize=(8, 7))
    ax.set_xscale('log')
    ax = sns.boxplot(data=last[numeric], orient='h', palette='Set1')
    ax.xaxis.grid(False)
    ax.set(ylabel='Feature names')
    ax.set(xlabel='Numeric values')
    ax.set(title='Numeric Distribution of Features')
    sns.despine(trim=True, left=True)

对数据的偏移进行修正，用scipy函数boxcox1p来计算Box-Cox转换，目标是使数据规范化

  # 寻找偏弱的特征
    from scipy.stats import skew, norm
 
    skew_features = last[numeric].apply(lambda x: skew(x)).sort_values(ascending=False)
    high_skew = skew_features[skew_features > 0.5]
    skew_index = high_skew.index
    skewness = pd.DataFrame({'Skew': high_skew})
    skew_features.head(10)
 
    # 用scipy函数boxcox1p来计算Box-Cox转换。我们的目标是找到一个简单的转换方式使数据规范化。
    from scipy.special import boxcox1p
    from scipy.stats import boxcox_normmax
 
    for i in skew_index:
        last[i] = boxcox1p(last[i], boxcox_normmax(last[i] + 1))
 
    # 处理所有的 skewed values
    sns.set_style('white')
    f, ax = plt.subplots(figsize=(8, 7))
    ax.set_xscale('log')
    ax = sns.boxplot(data=last[skew_index], orient='h', palette='Set1')
    ax.xaxis.grid(False)
    ax.set(ylabel='Feature names')
    ax.set(xlabel='Numeric values')

构造 logs 特征， squares 特征

    def logs(res, ls):
        m = res.shape[1]
        for l in ls:
            res = res.assign(newcol=pd.Series(np.log(1.01 + res[l])).values)
            res.columns.values[m] = l + '_log'
            m += 1
        return res
 
    def squares(res, ls):
        m = res.shape[1]
        for l in ls:
            res = res.assign(newcol=pd.Series(res[l] * res[l]).values)
            res.columns.values[m] = l + '_sq'
            m += 1
        return res

五、模型
自定义loss函数，实现线下、线上loss值偏差不大

# 由 loss 值计算score
def re_loglossv(labels,preds):
    deta = 3.45
    y_true = labels   # you can try this eval metric for fun
    y_pred = preds
    p = np.clip(y_pred, 1e-10, 1-1e-10)
    loss = -1/len(y_true) * np.sum(y_true * np.log(p) * deta + (1 - y_true) * np.log(1-p))
    return 're_logloss',loss,False

XGB模型参数设置：

    import xgboost as xgb
    # xgb 模型
    from sklearn.model_selection import KFold, RepeatedKFold, StratifiedKFold
    folds = StratifiedKFold(n_splits=5, shuffle=True, random_state=2019)
    # xgb模型参数设置
    xgb_params = {"booster": 'gbtree',
                  'eta': 0.005,
                  'max_depth': 5,
                  'subsample': 0.7,
                  'colsample_bytree': 0.8,
                  'objective': 'binary:logistic',
                  'eval_metric': 'logloss',
                  'silent': True,
                  'nthread': 8,
                  'scale_pos_weight': 2.5   # 处理正负样本不均衡
                  }
 
# -----------------------------------------------------------------------------------------------------------
 
    oof_xgb = np.zeros(len(X_train))
    predictions_xgb = np.zeros(len(X_valid))
    watchlist = [(xgb.DMatrix(X_train.as_matrix(), y_train.as_matrix()), 'train'),
                 (xgb.DMatrix(X_valid.as_matrix(), y_valid.as_matrix()), 'valid_data')]
    clf = xgb.train(dtrain=xgb.DMatrix(np.array(X_train), np.array(y_train)), num_boost_round=500, evals=watchlist,
                    early_stopping_rounds=200,
                    verbose_eval=100, params=xgb_params, feval=myFeval)
    oof_xgb = clf.predict(xgb.DMatrix(X_valid.as_matrix()), ntree_limit=clf.best_ntree_limit)
    pred_xgb = clf.predict(xgb.DMatrix(X_all.as_matrix()), ntree_limit=clf.best_ntree_limit)
    res = all_data[['customer_id']]
    res['result'] = pred_xgb
    # 保存 xgb模型
    # clf.save_model('./xgb.model_true_false')
    # load model
    # bst2 = xgb.Booster(model_file='xgb.model1')

对于XGB参数的调整
五折交叉验证：

  # 五折交叉验证
    for fold_, (trn_idx, val_idx) in enumerate(folds.split(train_x, train_y)):
        print("fold n°{}".format(fold_ + 1))
        trn_data = xgb.DMatrix(train_x[trn_idx], train_y[trn_idx])
        val_data = xgb.DMatrix(train_x[val_idx], train_y[val_idx])
        watchlist = [( trn_data, 'train'), (val_data, 'valid_data')]
        clf = xgb.train(dtrain=trn_data, num_boost_round=300, evals=watchlist, early_stopping_rounds=200,
                        verbose_eval=100, params=xgb_params, feval=myFeval)
        oof_xgb[val_idx] = clf.predict(xgb.DMatrix(train_x[val_idx]), ntree_limit=clf.best_ntree_limit)
        pred_xgb += clf.predict(xgb.DMatrix(X_all.as_matrix()), ntree_limit=clf.best_ntree_limit) / folds.n_splits