Gunnar-Farneback算法原理 & Farneback光流法在UCSD异常数据集上的Demo
Gunnar-Farneback算法
论文：Two-Frame Motion Estimation Based on Polynomial Expansion
会议：13th Scandinavian Conference on Image Analysis (SCIA 2003)
作者：Gunnar Farnebäck（Computer Vision Laboratory, Link¨oping University, SE-581 83 Link¨oping, Sweden）
备注：[email protected] http://www.isy.liu.se/cvl/
一、多项式展开
多项式展开的想法是把每个像素点的邻域都用多项式来表示：
（1）
其中A是对称矩阵，b是向量，c是常量。系数是根据邻域内信号值的加权最小二乘法估计出来的。权重由两个组成部分，称为确定性和适用性。确定性与邻近区域的信号值耦合，而适用性则根据点在邻域中的位置确定邻域中点的相对权重。
二、位移估计
由于每个邻域都可以用一个多项式来逼近，所以首先分析一个多项式经过平移后会发生什么变化。考虑以下二次多项式：
（2）
整体位移d个单位后得到信号
：
（3）
设二次多项式等式如下：
（4）
（5）
（6）
当
是非奇异矩阵时，可以解出
：
（7）
（8）
实际情况中，不存在整个信号表示为一个多项式以及这两个图像信号的全局平移，但上述公式(7)仍然适用于实际信号。
这里用局部多项式逼近方程(2)中的全局多项式。然后对两个图像做多项式展开，第一个图像对应系数为
，
和
，第二个图像同理。理想情况下，根据方程(4)应该有，但实际上应该求解近似值：
（9）
（10）
然后用
代替前面的全局变量：
（11）
下面开始解决邻域估计的问题。根据方程(11)可以对每个像素点进行运算，但考虑到庞大的运算量这样做显然不太现实。假设位移过程是缓慢进行的，那么应当尽可能的缩小
的邻域
的搜索范围并找到符合方程(11)的：
（12）
这里设
为像素点对应的权重函数，根据最小二乘法可得：
（13）
三、参数化位移场
为了提高算法鲁棒性，对于一些运动模式应该建立参数化模型。下面来构建带有8个参数的2D运动模型：
（15）
上式可以表示成：
（16）
（17）
（18）
带入到方程(12)中，即可得到加权最小二乘问题：
（19）
现在用
去索引像素点邻域中的坐标，用最小二乘法求解可以得出：
（20）
这里可以像前面一样分别计算出
和
，然后用
做加权平均求出位移。
四、利用先验信息
目前为止仍存在一个问题，就是两个信号在相同坐标下的局部多项式除了位移之外都是一致的。由于这里的多项式展开是局部模型，所以会随着在空间位移而发生变化，所以会引入(11)中的误差，且这个误差会随着位移的增大而增大。所以这里引入先验位移信息，即比较第一个信号在的多项展开式和第二个信号在
的多项展开式，其中
为先验位移四舍五入得出的整型值，这样就只需要计算出真实值和基于先验位移的预估值。
替代上面的(9)和(10)为：
（21）
（22）
其中，
（23）
五、迭代与多尺度位移估计
在算法中采用先验位移场的优势在于可以闭合循环并迭代。具备一个好的先验估计意味着相对位移更小，这反过来又可以提高位移估计的精度。这里考虑两种不同的方法，迭代位移估计和多尺度位移估计。
在这两种方法中，迭代估计一步的位移，作为下一步的先验位移。第一步中的先验位移场通常被初始化为零，除非有明确的信息。在第一种方法中，在所有迭代中使用相同的多项式展开系数，并且只需要计算一次。这存在一个问题是，如果第一次迭代位移（相对于先验位移）过大，输出的位移就不能期望得到改善，迭代也就失去了意义。通过在较粗的尺度上进行分析，可以减少位移过大的问题。这意味着我们对多项式展开具有高适用性。其结果是，该估计算法可以处理较大的位移，但同时精度却降低了。
多尺度位移估计方法，从一个较粗的尺度开始，得到一个粗略但合理的位移估计，接着通过逐级细化尺度获得越来越精确的估计。这样的缺点是需要重新计算每个尺度的多项式展开系数，但是可以通过在尺度变换之间进行二次采样来降低此成本。
Farneback光流法在UCSD异常数据集上的Demo
实验环境：Win10 | Python 3.7.3 | OpenCV 4.1.0
实验代码：
def draw_flow(im, flow, step=16):
# 在间隔分开的像素采样点处绘制光流
h, w = im.shape[:2]
y, x = mgrid[step/2:h:step, step/2:w:step].reshape(2, -1).astype(int)
fx, fy = flow[y, x].T
# 创建线的终点
lines = vstack([x, y, x+fx, y+fy]).T.reshape(-1, 2, 2)
lines = int32(lines)
# 创建图像并绘制
vis = cv2.cvtColor(im, cv2.COLOR_GRAY2BGR)
for (x1, y1), (x2, y2) in lines:
cv2.line(vis, (x1, y1), (x2, y2), (0, 255, 0), 1)
cv2.circle(vis, (x1, y1), 1, (0, 255, 0), -1)
return vis
# 省略N行代码......
# 提取第一帧
first_rgbframe = cv2.imread(frame_path + frames[0], 1)
del frames[0]
prev_gray = cv2.cvtColor(first_rgbframe, cv2.COLOR_BGR2GRAY)
for frame_i in frames:
rgbframe = cv2.imread(frame_path + frame_i, 1)
gray = cv2.cvtColor(rgbframe, cv2.COLOR_BGR2GRAY)
# 计算流
flow = cv2.calcOpticalFlowFarneback(prev_gray, gray, None, 0.5, 3, 15, 3, 5, 1.2, 0)
prev_gray = gray
drawImg = draw_flow(gray, flow)
cv2.imwrite(frameFB_path + frame_i, drawImg)
# 画出流矢量
cv2.imshow('Optical flow', drawImg)
if cv2.waitKey(10) == 27:
break
time.sleep(0.1)实验结果：
UCSDped1\Test\Test014
UCSDped2\Test\Test005
上面分别是UCSD anomaly dataset中的两个Test片段，可以看到人群或者单车/车辆经过的地方，绿色点都会伴随联动。
附录：
数据集链接：UCSD Anomaly Detection Dataset
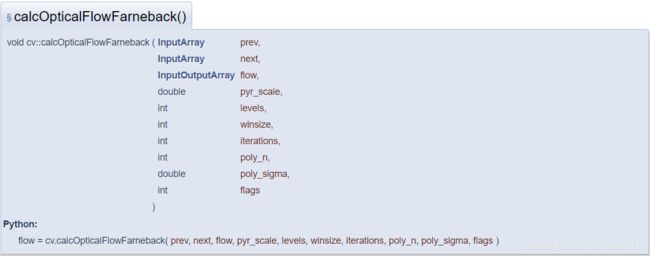
OpenCV - calcOpticalFlowFarneback() 参数解释：
prev：前一张8位单通道输入图像
next：后一张8位单通道输入图像
flow：计算得出的与输入图像大小一致且类型为CV_32FC2的光流图
pyr_scale：构建金字塔时图像的缩放系数(<1)；比如系数=0.5时是典型金字塔模型，没下一个层级图像为上一级的一半大小
levels：金字塔的层数；层数为1时表示没有额外的层级直接输入原图
winsize：平均窗口大小；窗口越大对于图像噪声越不敏感，能捕获到更多的快动作，但会产生更遗漏的动作场
iterations：每个金字塔层级中算法的迭代次数
poly_n：像素的邻域大小，邻域是为了做多项式展开的；邻域越大，表示图像越光滑，算法鲁棒性更强且运动场更模糊，标准参考值为5或者7
poly_sigma：用于平滑用作多项式展开基础的导数的高斯函数的标准差；poly_n=5时，可以设置poly_sigma为1.1；poly_n=7时，可以设置poly_sigma=1.5
flags：可以设置为以下两个标志之一
OPTFLOW_USE_INITIAL_FLOW：使用输入的光流图作为初始光流估计值
OPTFLOW_FARNEBACK_GAUSSIAN：使用高斯winsize×winsize滤波器代替相同大小的盒式滤波器进行光流估计；通常，此选项以较低的速度提供比盒式滤波器更精确的z流；通常，高斯窗口的winsize应设置为更大的值以达到相同的鲁棒性级别。
OpenCV官方原文解释：点击跳转到官方文档
参考资料：
1. Gunnar Farnebäck. Two-Frame Motion Estimation Based on Polynomial Expansion[C]// 13th Scandinavian Conference on Image Analysis (SCIA 2003). Springer-Verlag, 2003.
2. OpenCV官方文档