RNN LSTM GRU Attention transformer公式整理总结（超详细图文公式）

整理各种模型的公式，以后面试复习用

RNN

公式：
$h_t=f\left(W\cdot \left[h_{t-1},x_t\right]+b\right)$

LSTM

公式：
遗忘门：$f_t=\sigma \left(W_f\cdot \left[h_{t-1},x_t\right]+b_f\right)$
输入门：$i_t=\sigma \left(W_i\cdot \left[h_{t-1},x_t\right]+b_i\right)$
细胞状态：${\tilde{C}}_t=\tanh \left(W_C\cdot \left[h_{t-1},x_t\right]+b_C\right)$
细胞更新：$C_t=f_t\ast C_{t-1}+i_t\ast {\tilde{C}}_t$
输出门：$o_t=\sigma \left(W_o\left[h_{t-1},x_t\right]+b_o\right)$
输出：$h_t=o_t\ast \tanh \left(C_t\right)$

GRU

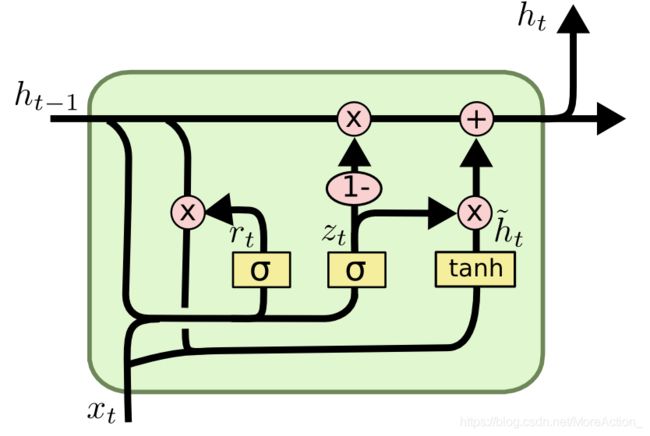
公式：
更新门：$z_t=\sigma \left(W_z\cdot \left[h_{t-1},x_t\right]\right)$
重置门：$r_t=\sigma \left(W_r\cdot \left[h_{t-1},x_t\right]\right)$
当前状态：${\tilde{h}}_t=\tanh \left(W\cdot \left[r_t\ast h_{t-1},x_t\right]\right)$
更新：$h_t=\left(1-z_t\right)\ast h_{t-1}+z_t\ast {\tilde{h}}_t$

Attention机制

Attention有很多计算方法，下面的公式只是比较常用的一种，计算方法和transformer中的qkv类似，下面公式以解码器第一个状态为例，Encoder输入长度为m，$\mathrm{W}$ 为参数，自动学习获得。

公式：
计算 $\mathrm{q}$：${\mathrm{q}}_0={\mathbf{W}}_Q\cdot {\mathrm{s}}_0$
计算 $\mathrm{k}$：${\mathrm{k}}_i={\mathbf{W}}_K\cdot {\mathbf{h}}_i,$ for $i=1$ to $m$
计算每个位置得分：${\tilde{\alpha }}_i={\mathrm{k}}_i^T{\mathrm{q}}_0,$ for $i=1$ to $m$
softmax归一化：$\left[{\alpha }_1,\cdots ,{\alpha }_m\right]=\mathrm{Softmax}\left(\left[{\tilde{\alpha }}_1,\cdots ,{\tilde{\alpha }}_m\right]\right)$（softmax公式想必很熟了）
最后，计算得到当前的 context vector：$c_0={\alpha }_1{\mathbf{h}}_1+\cdots +{\alpha }_m{\mathbf{h}}_m$

Transformer

transformer的公式不太好写，下面只给出几个关键公式

公式：
计算$Q、K、V$：$Q=W^Q\ast X$，$K=W^K\ast X$，$V=W^V\ast X$
计算self Attention：Attention $(Q,K,V)=\mathrm{softmax}\left(\frac{Q{K}^T}{\sqrt{d_k}}\right)V$
前馈网络层：$\mathrm{FFN}(Z)=\max \left(0,Z{W}_1+b_1\right)W_2+b_2$
位置编码：
$PE(pos,2i)=\sin \left(\frac{pos}{10000^{\frac{2i}{d_{model}}}}\right)$，$PE(pos,2i+1)=\cos \left(\frac{pos}{10000^{\frac{2i}{d_{model}}}}\right)$

上面公式只是一部分，其中还有一些细节 ，比如mutil-attention、残差&layer norm、decoder中的mask等。

transformer的核心组件就是Attention，代码实现是用上述矩阵乘的方式，为方便理解下面简述单个单词的Attention计算流程：

1. 根据embeding得到 $q,k,v$ 三个向量;
2. 用当前单词的$q$为其它每个单词计算一个score: \quad score $=q\cdot k$;
3. 为了避免score分布尖锐, 进行数值缩放, 即除以 $\sqrt{d_k}$
4. 对score进行softmax归一化;
5. 加权求和得到当前词的context vector $z:z=\sum {\alpha }_i{v}_i$

仔细观察，和上一节的Attention计算方式几乎一样。

持续更新中……