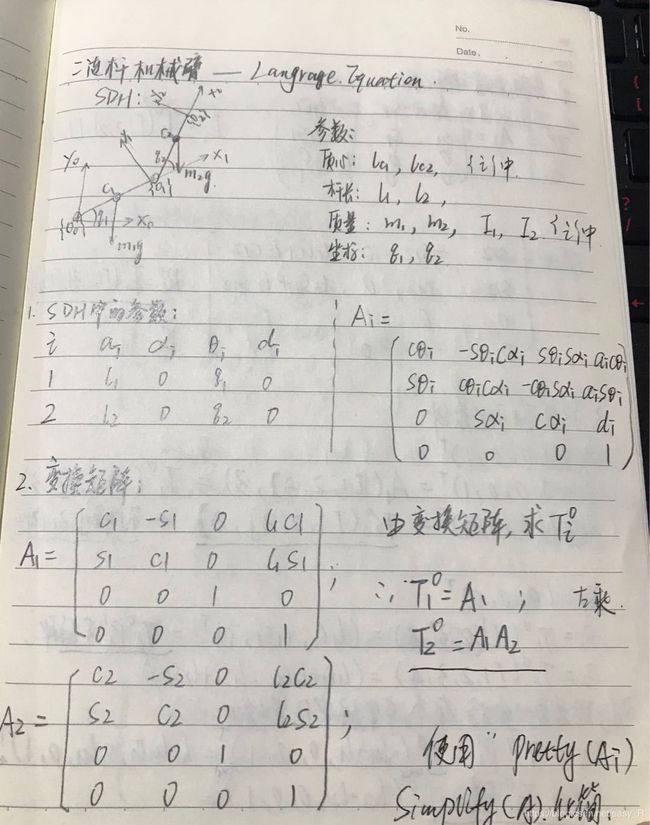
二连杆纯连杆动力学建模——LangrageEquation with Matlab
运用拉格朗日方程建立二连杆的纯连杆动力学方程,通过推导其过程明白原理。通过优化程序向多连杆动力学过度,方便后期计算n连杆动力学控制做基础。
我首先通过笔算整整算了10页纸,和参照书本结果一直。然后进行了逐步计算的matlab化,再然后通过代码优化循环,为后期的多连杆动力学做基础测试。
matlab code:
%test_for
%Two links dynamics
%method:Langrage Methods
%time:2019/02/26
%refence:《机器人建模和控制》 auth(Mark W.Spong)
%%
%%
%%
%使用拉格朗日方程计算两连杆动力学
%已知所有结构参数,10n个
%%
clear all;
clc;
close all;
tic;
%所有连杆参数使用符号计算
syms q1 alpha1 l1 lc1 m1 Ixx1 Iyy1 Izz1 Ixy1 Iyz1 Ixz1 real
syms q2 alpha2 l2 lc2 m2 Ixx2 Iyy2 Izz2 Ixy2 Iyz2 Ixz2 real
syms dq1 dq2 real
syms ddq1 ddq2 real
%%
%计算变换矩阵做准备
% A1=myfunSDHMatrix(l1,0,q1,0);
% A2=myfunSDHMatrix(l2,0,q2,0);
% T10=A1;
% T20=T10*A2;
%%
%**************************************************
%结构参数定义
a1=l1;a2=l2;
alpha1=0;alpha2=0;
d1=0;d2=0;
a=[a1,a2]';
alpha=[alpha1,alpha2]';
q=[q1,q2]';
ddq=[ddq1,ddq2]';
dq=[dq1,dq2]';
d=[d1,d2]';
%计算相邻矩阵间的变换矩阵Ai-1_i;
%相邻两个变换矩阵Ai_i-1=T(:,:,i);
%i坐标向基坐标的变换Ti_0=Ti-1_0*T(:,:,i);
n=2;
for k=1:n
A(:,:,k)=myfunSDHMatrix(a(k),alpha(k),q(k),d(k));
end
A00=eye(4);
for i=2:n
T(:,:,1)=A(:,:,1); %T10
T(:,:,i)=simplify(T(:,:,i-1)*A(:,:,i)); %Ti-1_0
end
%**************************************************
%%
% %旋转变换矩阵,为计算惯性张量做准备
% R10=T10([1,2,3],[1,2,3]);
% R20=T20([1,2,3],[1,2,3]);
%%
%**************************************************
%计算旋转变换矩阵为张量计算做准备
% for k=1:n
% R(:,:,k)=T(1:3,1:3,k); %计算Ri_0 ,后面计算直接被T矩阵替代
% end
%*************************************************
%连杆本体坐标系下的转动惯量
%连杆1的转动惯性I1
I1=[Ixx1,Ixy1,Ixz1;Ixy1,Iyy1,Iyz1;Ixz1,Iyz1,Izz1];
%连杆2的转动惯性I2
I2=[Ixx2,Ixy2,Ixz2;Ixy2,Iyy2,Iyz2;Ixz2,Iyz2,Izz2];
%三维矩阵下的惯性张量
In=cat(3,I1,I2);
%%
%计算雅克比矩阵Jvi,Jwi
%计算z方向坐标
% z0=[0,0,1]';
% z1=T10([1,2,3],3);
% z2=T20([1,2,3],3);
%%
%***************************************************
z0=[0,0,1]';
for k=1:n
Z(:,:,k)=T(1:3,3,k); %计算Z_i
end
%**************************************************
%计算o位置坐标
% o0=[0,0,0]';
% o1=T10([1,2,3],4);
% o2=T20([1,2,3],4);
%%
%**************************************************
o0=[0,0,0]'; %基坐标原点的位置
for k=1:n
o(:,:,k)=T(1:3,4,k); %计算o_i
end
%**************************************************
%%
% %计算质心位置oc在惯性坐标系中的坐标
% %杆1质心坐标,本体坐标(oc1x,oc1y,oc1z)
% oc1x=lc1-l1; oc1y=0; oc1z=0;
% oc1=simplify(T10*[oc1x,oc1y,oc1z,1]');
% %杆1质心坐标,本体坐标(oc2x,oc2y,oc1z)
% oc2x=lc2-l2; oc2y=0; oc2z=0;
% oc2=simplify(T20*[oc2x oc2y oc2z 1]');
%%
%***************************************************
%计算连杆质心在惯性坐标系中的位置坐标
%给出连杆质心在本体坐标中的位置坐标
oc1x=lc1-l1; oc1y=0; oc1z=0; %杆1
Pc1=[oc1x,oc1y,oc1z,1]'; %齐次化
oc2x=lc2-l2; oc2y=0; oc2z=0; %杆2
Pc2=[oc2x,oc2y,oc2z,1]';
%连杆质心坐标矩阵
Pc=[Pc1,Pc2]; %由已知条件给出
%计算Li在惯性坐标系中的位置坐标
for k=1:n
oc(:,:,k)=simplify(T(:,:,k)*Pc(1:4,k)); %计算oc_i
end
%****************************************************
% %求连杆1质心处的速度雅克比矩阵
% Jvc1=simplify([cross(z0,(oc1(1:3,:)-o0)),zeros(3,1)]);
% Jw1=[z0,zeros(3,1)];
% %求连杆2质心处的速度雅克比矩阵
% Jvc2=simplify([cross(z0,(oc2(1:3,:)-o0)),cross(z1,(oc2(1:3,:)-o1))]);
% Jw2=[z0,z1];
%%
%*****************************************************
%计算连杆雅克比矩阵
Jvc1=simplify([cross(z0,(oc(1:3,1,1)-o0)),zeros(3,1)]);
Jwc1=[z0,zeros(3,1)];
Jvc2=simplify([cross(z0,(oc(1:3,1,2)-o0)),cross(Z(:,:,1),(oc(1:3,1,2)-o(:,:,1)))]);
Jwc2=[z0,Z(:,:,1)];
%雅克比矩阵
%将独立计算得到的雅克比矩阵存入到三维矩阵
% for i=1:n
% Jvc(:,:,i)=eval(['Jvc',num2str(i)]) %批量存入二维雅克比线速度矩阵3 x n维,eval只对数值有效。如何处理符号????
% end
Jvc=cat(3,Jvc1,Jvc2); %cat 二维构建三维数组
Jwc=cat(3,Jwc1,Jwc2); %cat 二维构建三维数组
% Jwc=zeros(3,n,n)
% for i=1:n
% Jwc(:,:,i)=eval(['Jwc',num2str(i)]); %批量存入二维雅克比角速度矩阵3 x n维,eval只对数值有效。如何处理符号????
% end
%*****************************************************
% %%
% %计算连杆的平动动能
% %计算连杆1的平动动能
% Tt1=simplify(1/2*m1*(Jvc1).'*(Jvc1)); %移除dq
% %计算连杆2的平动动能
% Tt2=simplify(1/2*m2*(Jvc2).'*(Jvc2)); %移除dq
%
% %%
% %计算连杆的转动动能
% %计算连杆1的转动动能
% Tw1=simplify(1/2*(Jw1).'*(R10*I1*R10.')*(Jw1)); %移除dq
% %计算连杆2的转动动能
% Tw2=simplify(1/2*(Jw2).'*(R20*I2*R20.')*(Jw2)); %移除dq
%
% %%
% %计算惯性矩阵D(q)
% %D(q),惯性矩阵的计算相当于将动能项先移除dq项后累加的结果后2倍
% %这里为了计算方便将动能项的dq先移除
% D=simplify(2*(Tt1+Tt2+Tw1+Tw2));
%
%%
%*****************************************************************
%直接通过公式计算惯性矩阵D(q)
%D(q),initial matrix n x n
m=[m1,m2]';
D0=zeros(2);
D=D0;
for i=1:n
D=D+simplify([m(i).*Jvc(:,:,i).'*Jvc(:,:,i)+Jwc(:,:,i).'*T(1:3,1:3,i)*In(:,:,i)*T(1:3,1:3,i).'*Jwc(:,:,i)]);
end
disp('动力学方程中的惯量矩阵项D:');
D
%*****************************************************************
%%
% %%
% %根据D(q)计算Christoffel符号
% %根据i=1:n;j=1:n;k=1:n 分别计算一共计算n x n x n次/2
% c111=simplify(1/2*(diff(D(1,1),q1)+diff(D(1,1),q1)-diff(D(1,1),q1)));%i=1,j=1,k=1
% c112=simplify(1/2*(diff(D(2,1),q1)+diff(D(2,1),q1)-diff(D(1,1),q2)));%i=1,j=1,k=2
% c121=simplify(1/2*(diff(D(1,2),q1)+diff(D(1,1),q2)-diff(D(1,2),q1)));%i=1,j=2,k=1
% c122=simplify(1/2*(diff(D(2,2),q1)+diff(D(2,1),q2)-diff(D(1,2),q2)));%i=1,j=2,k=2
% c211=c121; %i=2,j=1,k=1
% c212=c122; %i=2,j=1,k=2
% c221=simplify(1/2*(diff(D(1,2),q2)+diff(D(1,2),q2)-diff(D(2,2),q1)));%i=2,j=2,k=1
% c222=simplify(1/2*(diff(D(2,2),q2)+diff(D(2,2),q2)-diff(D(2,2),q2)));%i=2,j=2,k=2
%
%%
%*****************************************************************
% %根据D(q)计算Christoffel符号
% c111=myfunChristoffel(2,D,1,1,1);
% c112=myfunChristoffel(2,D,1,1,2)
% c121=myfunChristoffel(2,D,1,2,1);
% c122=myfunChristoffel(2,D,1,2,2); n
% c211=myfunChristoffel(2,D,2,1,1);
% c212=myfunChristoffel(2,D,2,1,2);
% c221=myfunChristoffel(2,D,2,2,1);
% c222=myfunChristoffel(2,D,2,2,2);
%直接计算C矩阵
Cq=myfunTwolinkDirecC(2,D,q,dq);
disp('动力学方程中的离心及科里奥项Cq:')
Cq %n x n的矩阵
%******************************************************************
%%
% %%
% %重力势能计算G(k)
% % syms g real
% g=[0,-9.806,0]';
% %连杆1的重力势能
% P1=m1*g.'*oc1(1:3,:);
% %连杆2的重力势能
% P2=m2*g.'*oc2(1:3,:);
% %势能项g(k)
% P=P1+P2;
% g1=diff(P,q1);
% g2=diff(P,q2);
%%
%********************************************************************
%计算重力势能项
syms g real
g=[0,-9.806,0]';
P=0;
for k=1:n
P=P+m(k)*g.'*oc(1:3,:,k);
end
for i=1:n
gk(i)=diff(P,q(i)); %构造生成gk矩阵
end
%动力学方程中的动力项gk
gk=gk';
disp('动力学方程中的势能项g:');
gk
%********************************************************************
%%
% %%
% %连杆广义力计算
% %连杆1处的关节力矩
% tao1=simplify(D(1,1)*ddq1+D(1,2)*ddq2+c111*dq1*dq1+c121*dq1*dq2+c211*dq2*dq1+c221*dq2*dq2+g1);
% %连杆2处的关节力矩
% tao2=simplify(D(2,1)*ddq1+D(2,2)*ddq2+c112*dq1*dq1+c122*dq1*dq2+c212*dq2*dq1+c222*dq2*dq2+g2);
%
% %%
% %输出力矩值
% Taon=[tao1,tao2]';
% disp('肘型二连杆关节力矩输出Taon');
% % tao1
% % tao2
%
%%
%计算动力学方程
%动力学方程式:Dddq+C+gk=tao
tao=simplify(D*ddq+Cq*dq+gk);
%输出力矩值
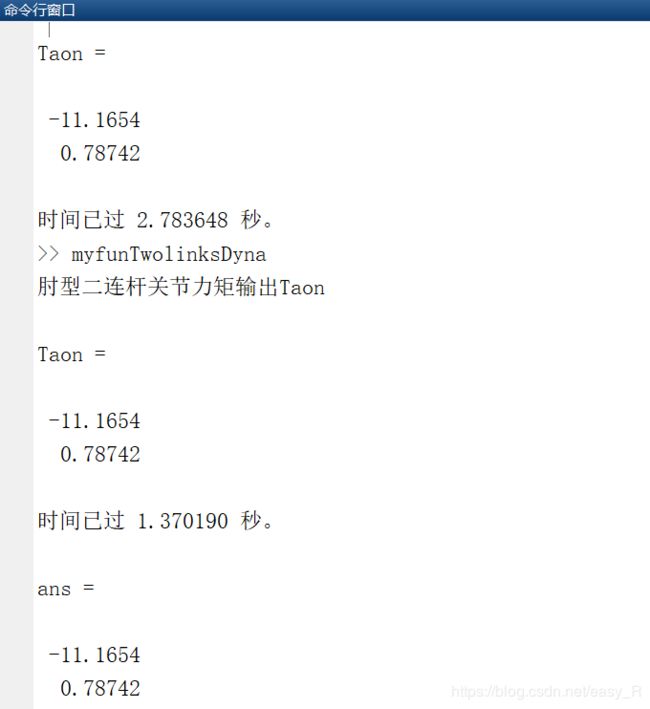
disp('二连杆关节力矩输出Taon:');
Taon=[tao(1),tao(2)]'
%%
%%
%************************************赋值计算******************************%
%数值计算
%进行结构参数赋值计算
dats={alpha1,l1,lc1,m1,Ixx1,Iyy1,Izz1,...
alpha2,l2,lc2,m2,Ixx2,Iyy2,Izz2};
datn={0,1,0.5,1,0,0,1/3,...
0,1,0.5,1,0,0,1/3};
Taon=vpa(subs(Taon,dats,datn),6);
%进行关节角度数值运算
dats_angle={q1,dq1,ddq1,...
q2,dq2,ddq2 };
datn_angle={pi/6,0.5,0.5,...
pi/3,0.25,0.45};
Taon=vpa(subs(Taon,dats_angle,datn_angle),6)
%**************************************************************************%
toc;
输出结果比较:
总结:
1.使用simplify进行化简
2.使用符号计算时候要注意尽量不要出现数值,否则报错‘sym canot trans to double’
更新:之前没有给出程序中的子函数,有人留言希望补全,故特意更新如下,希望对您有所帮助。
(其实我还做了6自由度机械臂的拉格朗日动力学方程,在这个二连杆的基础上应该很方便可以延伸得到六杆的,但是我的电脑计算这种纯符号整整需要花费大概五个小时,而且结果无法显示完全。我尝试打印出来,结果打印了几十页还是无法完全显示。最近忙于其他工作,后续我看看是否可以改进或者使用牛顿欧拉计算一下。后续更新欢迎交流!)
function Ai=myfunSDHMatrix(a,alpha,q,d)
%%
%Transform matrix in SDH coordinate
%Ai,is the transform matrix between two coordinate
Ai=[cos(q),-sin(q)*cos(alpha), sin(q)*sin(alpha),a*cos(q);
sin(q), cos(q)*cos(alpha),-cos(q)*sin(alpha),a*sin(q);
0, sin(alpha), cos(alpha), d;
0, 0, 0, 1
];
end
function Cq=myfunTwolinkDirecC(n,D,q,dq)
%%仅针对二连杆适用
% syms q1 q2
% syms dq1 dq2
% q=[q1,q2]';
% dq=[dq1,dq2]';
% C=zeros(n,n);
% Ct=zeros(1,n)
%计算C(k,j)项
for k=1:n
for j=1:n
for i=1:n
Ct(i)=1/2*((diff(D(k,j),q(i))+(diff(D(k,i),q(j)))-(diff(D(i,j),q(k)))))*dq(i);
end
C(k,j)=sum(Ct);
end
end
Cq=simplify(C);
endfunction c=myfunChristoffel(n,D,i,j,k)
%n,freedom of coordinate
%D,initial Matrix
%该函数仅仅针对两连杆模型
syms q1 q2
q=[q1,q2]';
c(i,j,k)=1/2*(diff(D(k,j),q(i))+diff(D(k,i),q(j))-diff(D(i,j),q(k)));
end