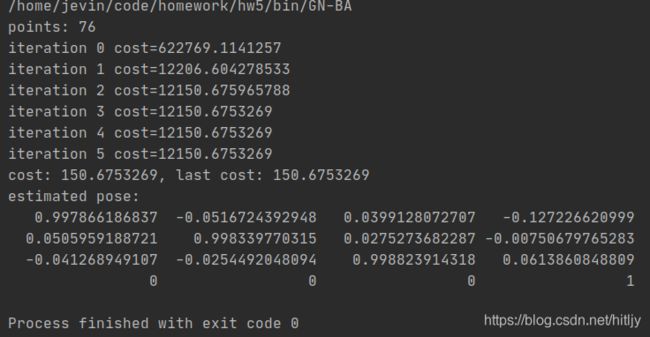
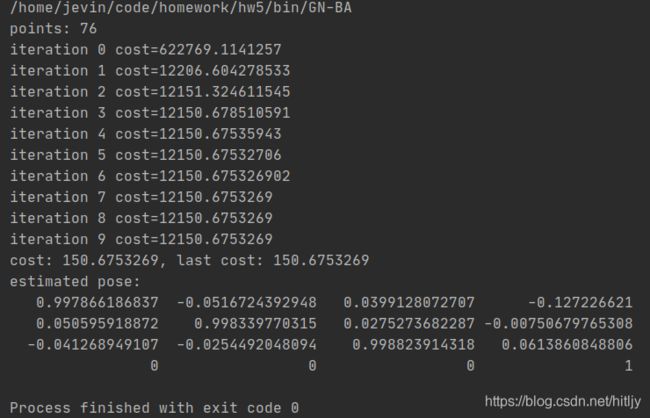
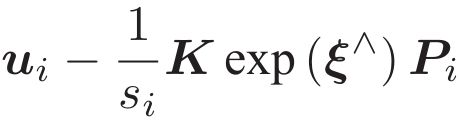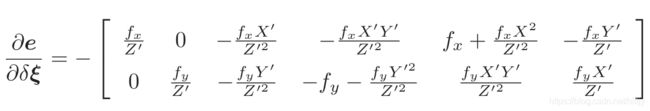深蓝学院视觉slam十四讲第5章作业

2.1

// compute the angle
void computeAngle(const cv::Mat &image, vector<cv::KeyPoint> &keypoints) {
    int half_patch_size = 8;
    for (auto &kp : keypoints) {
        float m01 = 0, m10 = 0;

        //从(u − 8, v − 8) 取到 (u + 7, v + 7)
        if (kp.pt.x < half_patch_size || kp.pt.y < half_patch_size ||
            kp.pt.x > image.cols - half_patch_size || kp.pt.y > image.rows - half_patch_size) {
            continue;
        }
        else{
            for(int row = -half_patch_size; row < half_patch_size; ++row){
                const auto *row_ptr = image.ptr<uchar>(kp.pt.y + row);
                for(int col = -half_patch_size; col < half_patch_size; ++col){
                    const auto *data_ptr = &row_ptr[size_t(kp.pt.x + col) * image.channels()];
                    uchar pixel = *data_ptr;
                    m10 += col * pixel;
                    m01 += row * pixel;
                }
            }
//            cout << "m10:" << m10 << " m01:" << m01 << endl;
        }
        kp.angle = std::atan2(m01,m10)/CV_PI*360; // compute kp.angle
        // END YOUR CODE HERE

//        cout << "kp.pt:" << kp.pt << " kp.size:" << kp.size << " kp.angle:" << kp.angle <<
//        " kp.response:" << kp.response << " kp.octave:" << kp.octave << " kp.class_id:" << kp.class_id << endl;
    }
    return;
}

计算角度后画出特征点结果：

2.2

// compute the descriptor
void computeORBDesc(const cv::Mat &image, vector<cv::KeyPoint> &keypoints, vector<DescType> &desc) {
//    int maxi = 0;
//    for(int i = 0; i < 256*4; i++)
//    {
//        if(abs(ORB_pattern[i]) > maxi){
//            maxi = abs(ORB_pattern[i]);
//        }
//    }
//    cout << "maxi:" << maxi << endl;
//    cout << "cos60:" << cos(60) << endl;
//    cout << "cos(CV_PI/3):" << cos(CV_PI/3) << endl;

    for (auto &kp: keypoints) {
        DescType d(256, false);
        bool IFOutBound = false;
        for (int i = 0; i < 256; i++) {
            cv::Point2f p(ORB_pattern[i * 4], ORB_pattern[i * 4 + 1]);
            cv::Point2f q(ORB_pattern[i * 4 + 2], ORB_pattern[i * 4 + 3]);

            float cos_theta = cos(kp.angle/360.0*CV_PI);
            float sin_theta = sin(kp.angle/360.0*CV_PI);

            // rotate with theta
            cv::Point2i pp = cv::Point2i(int(cos_theta * p.x - sin_theta * p.y + kp.pt.x), int(sin_theta * p.x + cos_theta * p.y + kp.pt.y));
            cv::Point2i qq = cv::Point2i(int(cos_theta * q.x - sin_theta * q.y + kp.pt.x), int(sin_theta * q.x + cos_theta * q.y + kp.pt.y));

            if (pp.x < 0 || pp.y < 0 || pp.x >= image.cols || pp.y >= image.rows ||
                qq.x < 0 || qq.y < 0 || qq.x >= image.cols || qq.y >= image.rows) {
                IFOutBound = true;
                continue;
            }
            d[i] = image.at<uchar>(pp.y, pp.x) <= image.at<uchar>(qq.y, qq.x);
	    // END YOUR CODE HERE
        }
        if(!IFOutBound){
            desc.push_back(d);
        }
        else{
            desc.push_back({});
        }
    }

    int bad = 0;
    int numd = 0;
    for (auto &d: desc) {
//        cout << "numd:" << numd << endl;
        numd++;
        if (d.empty()) bad++;
        else{
//            for(int i = 0; i < d.size(); i++){
//                cout << d[i] << " ";
//            }
            for(auto && i : d){
//                cout << i << " ";
            }
        }
//        cout << endl;
    }
    cout << "bad/total: " << bad << "/" << desc.size() << endl;
    return;
}

2.3

// brute-force matching
void bfMatch(const vector<DescType> &desc1, const vector<DescType> &desc2, vector<cv::DMatch> &matches) {
    double starttime = (double) cv::getTickCount();
    int d_max = 50;
    // START YOUR CODE HERE (~12 lines)
    // find matches between desc1 and desc2.
    for (int i1 = 0; i1 < desc1.size(); ++i1) {
        if (desc1[i1].empty()) continue;
        cv::DMatch m{i1, -1, 256};
        for (int i2 = 0; i2 < desc2.size(); ++i2) {
            if (desc2[i2].empty()) continue;
            int distance = 0;
            for (int j = 0; j < 256; j++) {
                distance += (desc1[i1][j] == desc2[i2][j])?0:1;
            }
//            cout << i1 << "test" << i2 << "distance:" << distance << endl;

            if (distance < d_max && distance < m.distance) {
                m.distance = distance;
                m.trainIdx = i2;
                cout << i1 << "match" << i2 << "distance:" << distance << endl;
            }
        }
        if (m.distance < d_max) {
            matches.push_back(m);
        }
    }
    // END YOUR CODE HERE

//    for (auto &m: matches) {
//        cout << m.queryIdx << ", " << m.trainIdx << ", " << m.distance << endl;
//    }
    double bfMatchtime = ((double) cv::getTickCount() - starttime) / cv::getTickFrequency();
    cout << "bfMatchtime: " << bfMatchtime << endl;
    return;
}

运行结果：
bfMatchtime: 0.125921
matches: 95

问题回答：

1. 因为ORB采用二进制的描述子用来描述每个特征点的特征信息
2. 50是经验值，取更大有更多误匹配，取更小匹配的点较少
3. 0.125921 秒，使用快速近似最邻近法（FLANN）可以减少时间

#include 
#include 
#include 

using namespace Eigen;

#include 

#include 

using namespace std;

int main(int argc, char **argv) {

    // 给定Essential矩阵
    Matrix3d E;
    E << -0.0203618550523477, -0.4007110038118445, -0.03324074249824097,
            0.3939270778216369, -0.03506401846698079, 0.5857110303721015,
            -0.006788487241438284, -0.5815434272915686, -0.01438258684486258;

    // 待计算的R,t
    Matrix3d R;
    Vector3d t;

    // SVD and fix sigular values
    // START YOUR CODE HERE
    Eigen::JacobiSVD<Matrix3d> svd(E,ComputeFullU|ComputeFullV); //svd分解
    Matrix3d U=svd.matrixU();
    Matrix3d V=svd.matrixV();
    Matrix3d SIGMA=U.inverse()*E*V.transpose().inverse();
    Vector3d sigma_value = svd.singularValues();
    Vector3d sigma_value2={(sigma_value[0]+sigma_value[1])/2,(sigma_value[0]+sigma_value[1])/2,0};
    Matrix3d SIGMA2=sigma_value2.asDiagonal();

    cout<<"SIGMA=\n"<<SIGMA<<endl;
    cout<<"sigma_value=\n"<<sigma_value<<endl;
    cout<<"SIGMA2=\n"<<SIGMA2<<endl;
    cout<<"sigma_value2=\n"<<sigma_value2<<endl;
    // END YOUR CODE HERE

    // set t1, t2, R1, R2 
    // START YOUR CODE HERE
    Matrix3d t_wedge1;
    Matrix3d t_wedge2;
    Matrix3d R1;
    Matrix3d R2;

    Matrix3d RZ1=AngleAxisd(M_PI/2,Vector3d(0,0,1)).toRotationMatrix();
    Matrix3d RZ2=AngleAxisd(-M_PI/2,Vector3d(0,0,1)).toRotationMatrix();
    t_wedge1=U*RZ1*SIGMA2*U.transpose();
    t_wedge2=U*RZ2*SIGMA2*U.transpose();
    R1=U*RZ1.transpose()*V.transpose();
    R2=U*RZ2.transpose()*V.transpose();

    // END YOUR CODE HERE

    cout << "R1 = " << R1 << endl;
    cout << "R2 = " << R2 << endl;
    cout << "t1 = " << Sophus::SO3d::vee(t_wedge1) << endl;
    cout << "t2 = " << Sophus::SO3d::vee(t_wedge2) << endl;

    // check t^R=E up to scale
    Matrix3d tR = t_wedge1 * R1;
    cout << "t^R = " << tR << endl;

    return 0;
}

#include 
#include 

using namespace Eigen;

#include 
#include 
#include 
#include 

#include "sophus/se3.hpp"

using namespace std;

typedef vector<Vector3d, Eigen::aligned_allocator<Vector3d>> VecVector3d;
typedef vector<Vector2d, Eigen::aligned_allocator<Vector3d>> VecVector2d;
typedef Matrix<double, 6, 1> Vector6d;

string p3d_file = "../p3d.txt";
string p2d_file = "../p2d.txt";

int main(int argc, char **argv) {

    VecVector2d p2d;
    VecVector3d p3d;
    Matrix3d K;
    double fx = 520.9, fy = 521.0, cx = 325.1, cy = 249.7;
    K << fx, 0, cx, 0, fy, cy, 0, 0, 1;

    // load points in to p3d and p2d 
    // START YOUR CODE HERE
    ifstream p3d_fin(p3d_file);
    ifstream p2d_fin(p2d_file);
    Vector3d p3d_input;
    Vector2d p2d_input;
    if (!p3d_fin) {
        cerr << "p3d_fin " << p3d_file << " not found." << endl;
    }
    while (!p3d_fin.eof()) {
        p3d_fin >> p3d_input(0) >> p3d_input(1) >> p3d_input(2);
        p3d.push_back(p3d_input);
    }
    p3d_fin.close();

    if (!p2d_fin) {
        cerr << "p2d_fin " << p2d_file << " not found." << endl;
    }
    while (!p2d_fin.eof()) {
        p2d_fin >> p2d_input(0) >> p2d_input(1);
        p2d.push_back(p2d_input);
    }
    p2d_fin.close();
    // END YOUR CODE HERE
    assert(p3d.size() == p2d.size());

    int iterations = 100;
    double cost = 0, lastCost = 0;
    int nPoints = p3d.size();
    cout << "points: " << nPoints << endl;

    Sophus::SE3d T_esti; // estimated pose

    for (int iter = 0; iter < iterations; iter++) {

        Matrix<double, 6, 6> H = Matrix<double, 6, 6>::Zero();
        Vector6d b = Vector6d::Zero();

        cost = 0;
        // compute cost
        for (int i = 0; i < nPoints; i++) {
            // compute cost for p3d[I] and p2d[I]
            // START YOUR CODE HERE 
            Eigen::Vector3d pc = T_esti * p3d[i];
            Eigen::Vector2d proj(fx * pc[0] / pc[2] + cx, fy * pc[1] / pc[2] + cy);
            Eigen::Vector2d e = p2d[i] - proj;

            cost += e.squaredNorm()/2;
	    // END YOUR CODE HERE

	    // compute jacobian
            Matrix<double, 2, 6> J;
            // START YOUR CODE HERE
            double inv_z = 1.0 / pc[2];
            double inv_z2 = inv_z * inv_z;
            J << -fx * inv_z,
                    0,
                    fx * pc[0] * inv_z2,
                    fx * pc[0] * pc[1] * inv_z2,
                    -fx - fx * pc[0] * pc[0] * inv_z2,
                    fx * pc[1] * inv_z,
                    0,
                    -fy * inv_z,
                    fy * pc[1] * inv_z2,
                    fy + fy * pc[1] * pc[1] * inv_z2,
                    -fy * pc[0] * pc[1] * inv_z2,
                    -fy * pc[0] * inv_z;
	    // END YOUR CODE HERE

            H += J.transpose() * J;
            b += -J.transpose() * e;
        }

	// solve dx 
        Vector6d dx;

        // START YOUR CODE HERE 
        dx = H.ldlt().solve(b);
        // END YOUR CODE HERE

        if (isnan(dx[0])) {
            cout << "result is nan!" << endl;
            break;
        }

        if (iter > 0 && cost >= lastCost) {
            // cost increase, update is not good
            cout << "cost: " << cost << ", last cost: " << lastCost << endl;
            break;
        }

        // update your estimation
        // START YOUR CODE HERE 
        T_esti = Sophus::SE3d::exp(dx) * T_esti;
        // END YOUR CODE HERE
        
        lastCost = cost;

        cout << "iteration " << iter << " cost=" << cout.precision(12) << cost << endl;
    }

    cout << "estimated pose: \n" << T_esti.matrix() << endl;
    return 0;
}

运行结果：

问题回答：

1. 3D点的投影位置与观测位置作差
   

3. 左乘或右乘微小扰动exp(dx)
   代码中给出左乘写法，下图为右乘写法运行结果，由于数值计算原因迭代次数更多
   

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 

using namespace std;
using namespace Eigen;
using namespace cv;

string trajectory_file = "../compare.txt";

void pose_estimation_3d3d(const vector<Point3f> &pts1,const vector<Point3f> &pts2, Eigen::Matrix3d &R_, Eigen::Vector3d &t_);
void DrawTrajectory(vector<Sophus::SE3d, Eigen::aligned_allocator<Sophus::SE3d>> poses_e,
        vector<Sophus::SE3d, Eigen::aligned_allocator<Sophus::SE3d>> poses_g,
        const string& ID);

int main(int argc, char **argv) {

    vector<Sophus::SE3d, Eigen::aligned_allocator<Sophus::SE3d>> poses_e;
    vector<Sophus::SE3d, Eigen::aligned_allocator<Sophus::SE3d>> poses_g;
    vector<Sophus::SE3d, Eigen::aligned_allocator<Sophus::SE3d>> poses_gt;
    vector<Point3f> pts_e,pts_g;
    ifstream fin(trajectory_file);
    if(!fin){
        cerr<<"can't find file at "<<trajectory_file<<endl;
        return 1;
    }
    while(!fin.eof()){
        double t1,tx1,ty1,tz1,qx1,qy1,qz1,qw1;
        double t2,tx2,ty2,tz2,qx2,qy2,qz2,qw2;
        fin>>t1>>tx1>>ty1>>tz1>>qx1>>qy1>>qz1>>qw1>>t2>>tx2>>ty2>>tz2>>qx2>>qy2>>qz2>>qw2;
        pts_e.push_back(Point3f(tx1,ty1,tz1));
        pts_g.push_back(Point3f(tx2,ty2,tz2));
        poses_e.push_back(Sophus::SE3d(Quaterniond(qw1,qx1,qy1,qz1),Vector3d(tx1,ty1,tz1)));
        poses_g.push_back(Sophus::SE3d(Quaterniond(qw2,qx2,qy2,qz2),Vector3d(tx2,ty2,tz2)));
    }

    Matrix3d R;
    Vector3d t;
    pose_estimation_3d3d(pts_e,pts_g,R,t);
    Sophus::SE3d T_eg(R,t);
    for(auto SE_g:poses_g)    {
        Sophus::SE3d T_e=T_eg*SE_g;
        poses_gt.push_back(T_e);
    }
    DrawTrajectory(poses_e,poses_g," Before Align");
    DrawTrajectory(poses_e,poses_gt," After Align");
    return 0;
}

void pose_estimation_3d3d(const vector<Point3f> &pts1,
                          const vector<Point3f> &pts2,
                          Eigen::Matrix3d &R_, Eigen::Vector3d &t_) {
    Point3f p1, p2;     // center of mass
    int N = pts1.size();
    for (int i = 0; i < N; i++) {
        p1 += pts1[i];
        p2 += pts2[i];
    }
    p1 = Point3f(Vec3f(p1) / N);
    p2 = Point3f(Vec3f(p2) / N);
    vector<Point3f> q1(N), q2(N); // remove the center
    for (int i = 0; i < N; i++) {
        q1[i] = pts1[i] - p1;
        q2[i] = pts2[i] - p2;
    }

    // compute q1*q2^T
    Eigen::Matrix3d W = Eigen::Matrix3d::Zero();
    for (int i = 0; i < N; i++) {
        W += Eigen::Vector3d(q1[i].x, q1[i].y, q1[i].z) * Eigen::Vector3d(q2[i].x, q2[i].y, q2[i].z).transpose();
    }
    cout << "W=" << W << endl;

    // SVD on W
    Eigen::JacobiSVD<Eigen::Matrix3d> svd(W, Eigen::ComputeFullU | Eigen::ComputeFullV);
    Eigen::Matrix3d U = svd.matrixU();
    Eigen::Matrix3d V = svd.matrixV();

    cout << "U=" << U << endl;
    cout << "V=" << V << endl;

    R_ = U * (V.transpose());
    if (R_.determinant() < 0) {
        R_ = -R_;
    }
    t_ = Eigen::Vector3d(p1.x, p1.y, p1.z) - R_ * Eigen::Vector3d(p2.x, p2.y, p2.z);
}

void DrawTrajectory(vector<Sophus::SE3d, Eigen::aligned_allocator<Sophus::SE3d>> poses_e,
        vector<Sophus::SE3d, Eigen::aligned_allocator<Sophus::SE3d>> poses_g,
        const string& ID) {
    if (poses_e.empty() || poses_g.empty()) {
        cerr << "Trajectory is empty!" << endl;
        return;
    }

    string windowtitle = "Trajectory Viewer" + ID;
    // create pangolin window and plot the trajectory
    pangolin::CreateWindowAndBind(windowtitle, 1024, 768);
    glEnable(GL_DEPTH_TEST);
    glEnable(GL_BLEND);
    glBlendFunc(GL_SRC_ALPHA, GL_ONE_MINUS_SRC_ALPHA);

    pangolin::OpenGlRenderState s_cam(
            pangolin::ProjectionMatrix(1024, 768, 500, 500, 512, 389, 0.1, 1000),
            pangolin::ModelViewLookAt(0, -0.1, -1.8, 0, 0, 0, 0.0, -1.0, 0.0)
    );

    pangolin::View &d_cam = pangolin::CreateDisplay()
            .SetBounds(0.0, 1.0, pangolin::Attach::Pix(175), 1.0, -1024.0f / 768.0f)
            .SetHandler(new pangolin::Handler3D(s_cam));


    while (pangolin::ShouldQuit() == false) {
        glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);

        d_cam.Activate(s_cam);
        glClearColor(1.0f, 1.0f, 1.0f, 1.0f);

        glLineWidth(2);
        for (size_t i = 0; i < poses_e.size() - 1; i++) {
            glColor3f(1.0f, 0.0f, 0.0f);
            glBegin(GL_LINES);
            auto p1 = poses_e[i], p2 = poses_e[i + 1];
            glVertex3d(p1.translation()[0], p1.translation()[1], p1.translation()[2]);
            glVertex3d(p2.translation()[0], p2.translation()[1], p2.translation()[2]);
            glEnd();
        }
        for (size_t i = 0; i < poses_g.size() - 1; i++) {
            glColor3f(0.0f, 0.0f, 1.0f);
            glBegin(GL_LINES);
            auto p1 = poses_g[i], p2 = poses_g[i + 1];
            glVertex3d(p1.translation()[0], p1.translation()[1], p1.translation()[2]);
            glVertex3d(p2.translation()[0], p2.translation()[1], p2.translation()[2]);
            glEnd();
        }
        pangolin::FinishFrame();
        usleep(5000);   // sleep 5 ms
    }
}

运行结果：