自然语言处理（十四）——隐马尔科夫模型（HMM）初步理解

一、前言

本文主的目的是对隐马尔科夫模型进行初步的理解，也就是明白这个隐马尔科夫模型到底是个什么东西，明报这个隐马尔科夫模型到底有什么用。至于怎么利用这个马尔科夫模型做一个解决语音识别领域问题的小成品，本文还没有涉及，本人水平有限，正处在小白学习的阶段，因此有什么错误的地方，望各位不吝赐教。下面进入正题，这里用知乎一位答主的例子黄以及志洪老师课程来理解隐马尔科夫模型。

二、骰子案例来理解HMM

一般地,一个HMM记为一个五元组μ=(S,K,A,B,π),其中,S为状态的集合,K为输出符号的集合π,A和B分别是初始状态的概率分布、状态转移概率和符号发射概率。为了简单,有时也将其记为三元组μ= (A,B,π)。
下面用骰子这个例子来对应一下五元组。

下面这三个骰子分别是正方体骰子（记为D6，有六个面，每个面的概率都是1/6），正四面体骰子（记为D4，每个面的概率都是1/4），正八面体骰子（记为D8，每个面的概率都是1/8）。

五元组中S对应的就是三种骰子｛D6，D4，D8｝

五元组中K对应的就是三种骰子能够投掷出的结果｛1，2，3，4，5，6，7，8｝

五元组中π是一个向量，对应的就是人开始掷骰子，拿到哪个骰子的概率。显而易见，拿到每个骰子的概率都是1/3。因此π=

五元组中A是状态转移概率，首先，写这个例子的答主非常细致，思维非常缜密，下面一个马尔科夫链来直观看转移状况。

因此A = 

五元组中B是符号发射概率，

以上的内容介绍了这个五元组的符号各自代表着什么，不过现在该解释为什么叫隐马尔科夫模型？隐到底隐在哪里？

假如我们掷骰子，掷了若干次，得到一个点数的序列：1 6 3 5 2 7 3 5 2 4。这个序列叫可见状态链，那么这些点数到底由哪个骰子掷出来的？这个我们是看不见的，因此，骰子的序列就是隐含的状态链。

这个例子举得非常巧妙，很容易的让人理解隐马尔科夫的隐到底是什么。

明白了隐马尔科夫模型是什么？接下来就该介绍，马尔科夫模型能用来干什么？接下来用语音识别的案例来解释一下这东西能干什么。

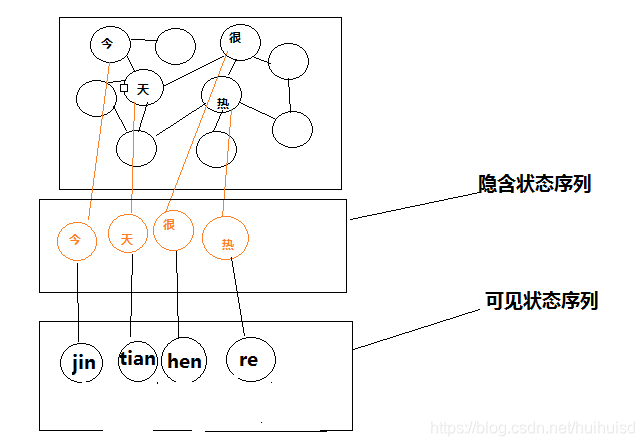
（1），如下图所示，用户说了一段语音，有人说了普通话jin  tian  hen  re  有人说了江西话jin tian  hen  le，现在已知隐含状态的数量（基元），知道转换概率（每个基元组合的概率）。现在可以计算P（jin  tian  hen  re ）和P（jin tian  hen  le），概率大的就当作是正确的。

（2）如下图所示，现在知道了语音是jin  tian  hen  re 已知隐含状态的数量（基元），知道转换概率（每个基元组合的概率）。要解决的问题就是，得到发出这些读音的到底是哪些字？得到最优解。

（3）汉字有很多多音字，例如“的”，有de音，有di音，计算发de音的概率和di的概率。

以上三点就是隐马尔科夫模型能干的一些事情，隐马尔科夫模型确实有点不好理解，今后还需要再多加研究。

参考的资料：宗成庆《统计自然语言处理》、https://www.zhihu.com/question/20962240、黄志洪老师自然语言处理课程资料。