吴恩达深度学习课程疑难点笔记系列-改善深层神经网络-第3周
本笔记系列参照吴恩达深度学习课程的视频和课件,并在学习和做练习过程中从CSDN博主何宽分享的文章中得到了帮助,再此表示感谢。
本周主要学习的内容有:
调试处理、为超参数选择合适的范围、正则化网络的激活函数、将Batch Norm拟合进神经网络、测试时的Batch Norm、Softmax回归、训练一个Softmax分类器、深度学习框架TensorFlow
本周学习的疑难点:
为超参数选择合适的范围、正则化网络的激活函数、将Batch Norm拟合进神经网络、测试时的Batch Norm
1.超参数调试优先级
模型训练过程中,需要我们对很多超参数进行调试,而那么多超参数,我们肯定不能同等对待,因此,按照吴老师的经验,我们一般把超参数调试分为以下优先级(从高往下)
- 学习速率 α \alpha α
- 动量梯度参数 β \beta β,隐藏单元数(hidden_units),小批量样本大小(mini-batch size)
- 学习速率衰减(learning_rate decay)、网络层数(layers)
- 建议调整为固定值的参数,比如:Adam算法中的 β 1 = 0.9 β 2 = 0.999 ϵ = 1 0 − 8 \beta_1=0.9 \beta_2=0.999 \epsilon=10^{-8} β1=0.9β2=0.999ϵ=10−8
调试超参数时,建议不要使用网格法,而是使用随机取值法,并在随机取值的过程中,先粗调再细调的方法。如图1、图2所示

图 1 图1 图1

图 2 图2 图2
选择参数范围时尽量使用对数表示,因为参数的可选范围跨越了好几个数量级,只有用对数可以在横轴上均匀表示。如图3所示

图 3 图3 图3
比如:学习速率 α \alpha α的取值范围可以是(0.00001,1),如果直接在横轴上表示的话,会导致取值不均匀,改用对数法取值,就可以解决这个问题,图3中的例子我们给 α \alpha α这样取值:
r = -4 * np.random.rand()
learning_rate = pow(10,r)
另外,根据我们训练设备的能力,我们可以选择Panda模式或者Caviar模式(熊猫模式或鱼子酱模式),如果设备处理能力一般,我们最好是选择熊猫模式,即一次训练一个模型;如果设备的处理能力还不错,我们可以选择鱼子酱模式,即一次训练多个模型,那样我们可以在不同的模型中使用不同的参数。
2.正则化网络的激活函数
上一周吴老师的课程里已经提到了正则化输入,这周的正则化网络的激活函数的概念其实和它类似,将神经网络层的激活函数值进行正则化,这样可以让神经网络更加稳定,因为这样不管 l − 1 l-1 l−1层函数的激活函数值实际分布如何变化,正则化后,他们都变成偏差为 u u u,方差为 δ \delta δ的分布。
对于给定的一些神经网络迭代值 Z 1 , Z 2 , . . . Z m Z^{1},Z^{2},...Z^{m} Z1,Z2,...Zm,进行正则化网络的激活函数后有:
u = 1 m ∑ i m Z ( i ) (1) u = \frac{1}{m} \sum_i^{m}Z^{(i)}\tag{1} u=m1i∑mZ(i)(1)
δ 2 = 1 m ∑ i m ( Z − u ) 2 (2) \delta ^2 = \frac{1}{m} \sum_i^m(Z-u)^2\tag{2} δ2=m1i∑m(Z−u)2(2)
Z n o r m i = Z i − u δ 2 + ϵ (3) Z_{norm}^i = \frac {Z^i-u}{\sqrt {\delta^2+\epsilon}}\tag{3} Znormi=δ2+ϵZi−u(3)
我们令均值 β = u \beta = u β=u,方差 γ = δ 2 + ϵ \gamma = \sqrt {\delta^2+\epsilon} γ=δ2+ϵ,则会得到
Z ~ ( i ) = γ Z n o r m i + β (4) \widetilde{Z}^{(i)} = \gamma Z_{norm}^{i}+\beta \tag{4} Z (i)=γZnormi+β(4)
以上如图4所示

图 4 图4 图4
将批正则化(Batch Norm)拟进神经网络的如图5、图6、图7所示
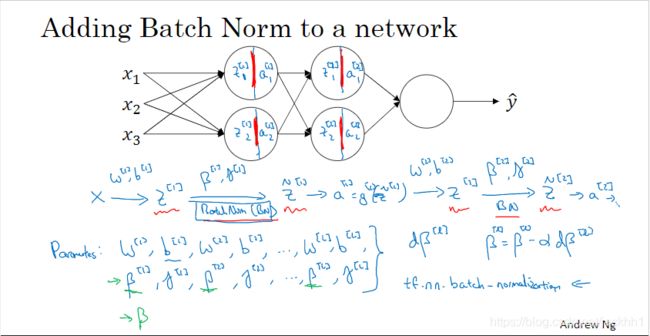
图 5 图5 图5
图5中的计算过程,在TF框架中我们可以用API:tf.nn.batch_normalization来表示。

图 6 图6 图6
从图6可以看出,参数b在批正则化后减掉了,所以可以忽略掉。
将batch nomalization运用到神经网络中具体流程,如图7所示

图 7 图7 图7
3.测试集上的Batch Norm
测试集可能没有训练集那么多样本,所以进行批正则化可能没有多大意义,因此,针对测试集,要计算均值和方差可以用指数加权平均来得到。具体操作过程,
在训练时针对每个mini_batch: X { 1 } , X { 2 } , X { 3 } . . . . . . X^{\{1\}},X^{\{2\}},X^{\{3\}}...... X{1},X{2},X{3}......, X { 1 } X^{\{1\}} X{1}在l层的激活网络函数的均值为 u { 1 } [ l ] u^{\{1\}[l]} u{1}[l], X { 2 } X^{\{2\}} X{2}在l层的激活网络函数的均值为 u { 2 } [ l ] u^{\{2\}[l]} u{2}[l], X { 3 } X^{\{3\}} X{3}在l层的激活网络函数的均值为 u { 3 } [ l ] u^{\{3\}[l]} u{3}[l],同理 δ 2 \delta^2 δ2,针对一个测试样本它的均值 u , δ 2 u,\delta^2 u,δ2我们可以采用结合训练时得到的 u , δ 2 u,\delta^2 u,δ2指数加权平均得到
4.softmax回归算法其实主要抓住这一点,模型每次输出的判断是根据 Y ^ \hat{Y} Y^中的最大值来定的,而 Y ^ \hat{Y} Y^中所有值加起来的和为1
5、用TensorFlow框架编写程序的思维步骤
- 创建还未执行/评价的张量(变量)(Tensor(variable))
- 编写张量(Tensor)间的操作
- 初始化我们的张量(Tensor)
- 创建会话(Session)
- 运行会话(Session),运行我们上面编写的四个步骤的内容。
本周的作业里用TensorFlow框架编写手势识别模型的基本操作思路如下:
(1)导入相关库
(2)导入数据、特征处理、特征缩放等
(3)创建placeholder(张量):create_placeholders(n_x, n_y)
(4)初始化参数:initialize_parameters(),得到的parameters是一个字典,跟之前用numpy编模型是一样的
(5)前向传播:forward_propagation(X,parameters)
(6)计算cost:compute_cost(Z3,Y),TensorFlow框架直接用Z3就可以计算代价函数了,所以这个地方要注意!
(7)反向传播:到这一步就开始与我们从头开始一步步写模型的方式大不同的地方,我们不需要再一步步地算每一层的导数了!
框架提供的反向传播方法:
optimizer = tf.train.GradientDescentOptimizer(learning_rate = learning_rate).minimize(cost)
运行方法:
_ , c = sess.run([optimizer, cost], feed_dict={X: minibatch_X, Y: minibatch_Y})
(8)构建模型:最后一步就是搭建模型了,在模型函数里调用上面的函数
model(X_train, Y_train, X_test, Y_test, learning_rate = 0.0001,num_epochs = 1500, minibatch_size = 32, print_cost = True)
使用TensorFlow框架要注意“会话”(Session)的使用,因为TF都是用会话来执行图运算的,比如运算张量、操作等。不过,TF2.0中已经没有会话了,详情可以参考我翻译的相关TF2.0官方指南系列笔记
