准确度、精确度、召回率、ROC曲线、AUC值

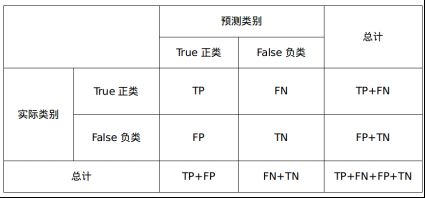
在介绍这些概念之前，先来看一下混淆矩阵：

TP: True Positive,将正类预测类正类的样本数量（预测正确）
FN: False Negtive,将正类预测为负类的样本数量（type II error, 漏报）
FP: False Positive,将负类预测为正类的样本数量（type I error）
TN: True Negtive,将负类预测为负类的样本数量（预测正确）

• 准确度：准确度表示分类正确的样本数所占比例

$$ACC=\frac{TP+TN}{TP+TN+FP+FN}$$

• 精确度、精度：该概念是针对“预测结果”而言的。表示预测为正类的样本中有多少是真的正样本

$$P=\frac{TP}{TP+FP}$$

• 召回率：该概念是针对“原始样本”而言的。表示样本中的正例有多少被分类正确了

$$R=\frac{TP}{TP+FN}$$

在知乎上看到一个图可以很好的理解：（点击查看原文）

• ROC曲线：
  在介绍ROC曲线之前，还需要引入其他概念：

1.敏感性Sensitivity、召回率Recall、hit rate、TPR（True Positive Rate）：表示样本中正类被分类正确的比例

$$TPR=\frac{TP}{TP+FN}$$
2.假阴性率FNR（False Negative Rate）:

$$FNR=\frac{FN}{TP+FN}=1-TPR$$
3.假阳性率FPR（False Positive Rate）：

$$FPR=\frac{FP}{FP+TN}=1-TNR$$
4.特异性specificity、真阴性率TNR（True Negative Rate）：表示样本中负类被分类正确的比例

$$TNR=\frac{TN}{FP+TN}$$

  ROC（Receiver Operating Characteristic Curve）接受者特征曲线，是反应敏感性和特异性连续变量的综合指标。
  ROC曲线图的横坐标是FPR，表示预测为正但实际为负的样本占所有负例样本的比例，纵坐标是TPR，，表示预测正类中实际负类就越多，纵坐标为TPR，表示预测为正且实际为正的样本占所有正例样本的比例，其值越大，表示预测正类中实际正类就越多。所以理想情况下，TPR应该越接近1越好，FPR越接近0越好。

  经过上面的描述我们知道，ROC曲线的横坐标和纵坐标其实是没有相关性的，所以不能把ROC曲线当做一个函数曲线来分析，应该把ROC曲线看成无数个点，每个点都代表一个分类器，其横纵坐标表征了这个分类器的性能。为了更好的理解ROC曲线，我们先引入ROC空间，如下图所示。

其中，A,B,C,C’为四个分类器，其工作结果如下：

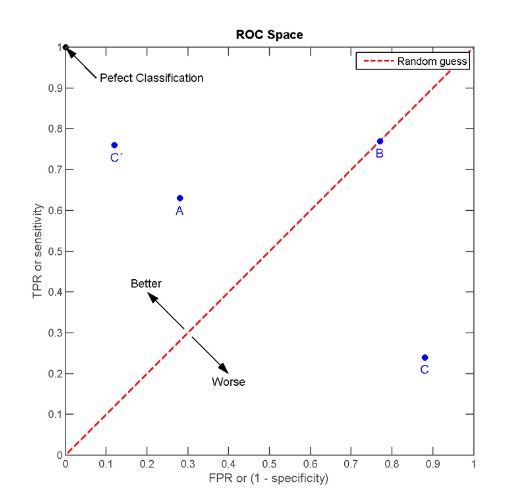
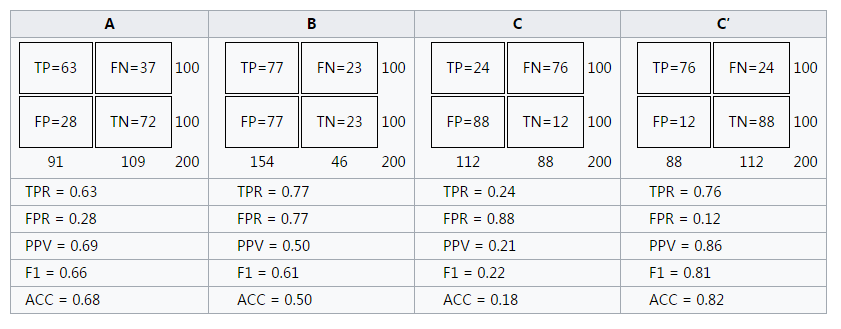
  明显的，C’的性能最好。而B的准确率只有0.5，几乎是随机分类。特别的，图中左上角坐标为（1,0）的点为完美分类点（perfect classification），它代表所有的分类全部正确，即归为1的点全部正确（TPR=1），归为0的点没有错误（FPR=0）。

  通过ROC空间，我们明白了一条ROC曲线其实代表了无数个分类器。那么我们为什么常常用一条ROC曲线来描述一个分类器呢？仔细观察ROC曲线，发现其都是上升的曲线（斜率大于0），且都通过点（0,0）和点（1,1）。其实，这些点代表着一个分类器在不同阈值下的分类效果，具体的，曲线从左往右可以认为是阈值从1到0的变化过程。当分类器阈值为1，代表不加以识别全部判断为False负类，此时TP=FP=0，$TPR=TP/（TP+FN）=0$，$FPR=FR/(FP+TN)=0$；当分类器阈值为0，代表不加以识别全部判断为True正类，此时FN=TN=0，$TPR=TP/（TP+FN）=1$，$FPR=FR/(FP+TN)=1$。所以，ROC曲线描述的其实是分类器性能随着分类器阈值的变化而变化的过程。对于ROC曲线，一个重要的特征是它的面积，面积为0.5为随机分类，识别能力为0，面积越接近于1识别能力越强，面积等于1为完全识别，该面积值用AUC值表示。

  下图中的实线为ROC曲线，线上的每个点表示一个阈值。
  在一个二分类模型中，假设采用逻辑回归分类器，其给出针对每个实例为正类的概率，那么通过设定一个阈值如0.6，概率大于等于0.6的为正类，小于0.6的为负类。对应的就可以算出一组(FPR,TPR)，在平面中得到对应坐标点。随着阈值的逐渐减小，越来越多的实例被划分为正类，但是这些正类中同样也掺杂着真正的负实例，即TPR和FPR会同时增大。阈值最大时，对应坐标点为(0,0)，阈值最小时，对应坐标点(1,1)。

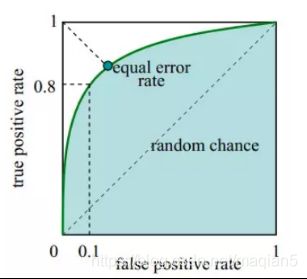
• AUC值：表示ROC曲线下的面积，即ROC曲线与x轴、（1，0）-（1，1）围绕的面积

参考：
1.简书zhwhong：https://www.jianshu.com/p/c61ae11cc5f6
2.知乎李云浩：https://zhuanlan.zhihu.com/p/26293316
3.知乎Charles Xiao：https://www.zhihu.com/question/19645541
4.CSDN nana-li:https://blog.csdn.net/quiet_girl/article/details/70830796