算法基础——动态规划之0-1背包问题
-
问题描述
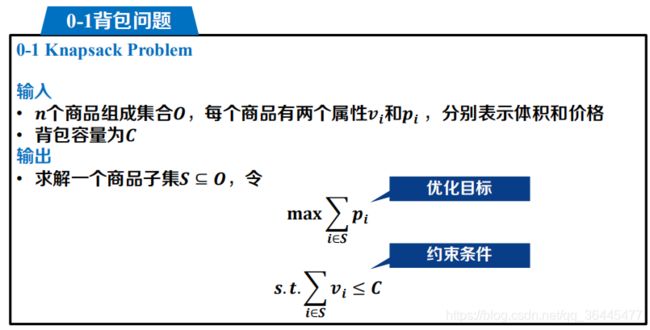
解决这个问题,最先想到的一定是暴力搜索:假设一共有n件商品,每件商品都有选择或不选两种状态,所有的选择方式为——从n件商品任取一件、任取两件、’’’、任取n件, 即共有Cn1 + Cn2 + Cn3 +…+Cnn 种选择方式。其中某些选择方式会超出背包的容量,把这样的选择方式剪掉,在剩余合法的选择方式中找到商品总价值最高的组合。我们采用递归的方式来进行暴力搜索:对于n件商品的情况,第i件商品的重量为w[i],价值为v[i],背包容量为c,计算n件商品的最高价值选择P(n,c)即为:
max{P(n-1,c-w[n])+v[n], P(n-1, c)}
P(n-1,c-w[n])+v[n]: 将第n件物品放入背包时的最高价值选择(选择了第n件物品后背包容量-w[n],再去找前n-1件物品的最高价值P(n-1,c-w[n]))
P(n-1, c):不选择第n件物品,背包容量仍为c不变。
const negInfinity = -1000
/*暴力搜索的求解方式(递归)*/
func KnapsackSR(w []int, v []int, flag []int,n int, c int) int {
// 背包体积为c,且在前n个商品中做选择
//递归边界
if c < 0 { //背包容量不足
return negInfinity
}
if n <= 0 { //商品不足 决策已经完成
return 0
}
getN := KnapsackSR(w,v,flag,n-1,c-w[n])+v[n]
noN := KnapsackSR(w,v,flag,n-1,c)
if getN > noN {
flag[n] = 1
return getN
} else {
flag[n] = 0
return noN
}
}
图解这种方法:可以发现在递归的过程中做了很多无用功——很多子问题是重复的,复杂度为O(2^n)
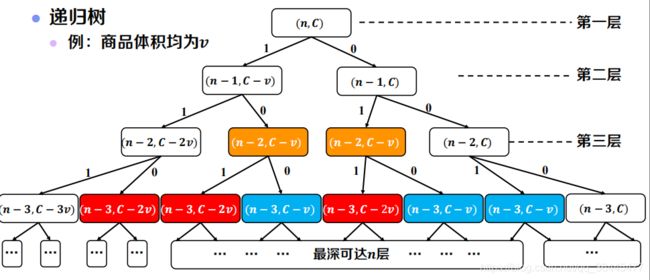
优化——带备忘录的递归
可以放置一张二维数组,记录计算过的子问题,避免重复计算:
 伪代码及实现如下:
伪代码及实现如下:
 e.g. Golang实现中数组计算是从下标为1开始的,由于数组下标从0开始,因此需要对数组的零号位进行填充:如商品重量数组为{1,2,3,4,5};则函数中传入的重量数组应为w := []int{0,1,2,3,4,5}(len(w)=6)
e.g. Golang实现中数组计算是从下标为1开始的,由于数组下标从0开始,因此需要对数组的零号位进行填充:如商品重量数组为{1,2,3,4,5};则函数中传入的重量数组应为w := []int{0,1,2,3,4,5}(len(w)=6)
//MR备忘录记录重复子问题的解
func KnapsackMR(w []int, v []int, flag []int, MR [][]int, n int, c int) int{
if c < 0 { //背包容量不足
return negInfinity
}
if n <= 0 { //商品不足 决策已经完成
return 0
}
//若备忘录中已记录过此子问题 则直接查询备忘录返回结果
if MR[n][c] != 0 {
return MR[n][c]
}
getN := KnapsackSR(w,v,flag,n-1,c-w[n])+v[n]
noN := KnapsackSR(w,v,flag,n-1,c)
max := 0
if getN > noN {
flag[n] = 1
max = getN
} else {
flag[n] = 0
max = noN
}
MR[n][c] = max
return max
}
动态规划的求解方法:
带备忘录的递归求解,本质上还是递归的方法:求解过程先从原问题自顶向下分解子问题,在自底向上由子问题的解得到原问题的解,再次优化:省略掉自顶向下的分解过程,直接自底向上计算即可,这就是动态规划的方法。
由递归式:P(n,c) = max{P(n-1,c-w[n])+v[n], P(n-1, c)}可以看出P(n,c)是由于P(i,j), i 那么可以设置一张二维数组表P[n][c],先对表进行初始化(当商品数为0或背包容量为0时,最高价值P一定为0:因此P(0,j)和P(i,0)均为0) 而后从上到下、从左往右依照递推式P(n,c) = max{P(n-1,c-w[n])+v[n], P(n-1, c)}依次计算出数组各个位置的值,最后得到的P[n][c]即为背包容量为c、商品个数为n时的最高价值。 求解获的最高价值时,背包里的商品选择组合的伪代码及实现如下: 最后,动态规划和分治问题有点类似:都是将问题划分为子问题求解,那么他们有什么不同呢: 1)动态规划是一个最优解问题: dp的目的是求一个问题的最优解,这类问题具有最优子结构性质,即最终问题的最优解由相关子问题的最优解组合而成,子问题可以独立求解。往往表现为一个递推式的形式 dp问题的基本求解步骤:分析问题结构->获得递推式->自底向上计算(填充二维数组)->最优方案追溯(TraceRecTable)func KnapsackDP(w []int, v []int, DPTable [][]int, RecTable [][]int, n int, c int) {
for i:=1; i<=n; i++ {
for j:=1; j<=c; j++ {
if j-w[i]>=0 && (DPTable[i-1][j-w[i]]+v[i]>DPTable[i-1][j]) {
DPTable[i][j] = DPTable[i-1][j-w[i]] + v[i]
RecTable[i][j] = 1
} else {
DPTable[i][j] = DPTable[i-1][j]
RecTable[i][j] = 0
}
}
}
}

func TraceRecTable(RecTable [][]int, w []int, n int, c int) {
if n <= 0 {
return
}
if RecTable[n][c] == 1 {
fmt.Println(n, " is Chosen")
TraceRecTable(RecTable, w, n-1, c-w[n])
} else {
TraceRecTable(RecTable, w, n-1, c)
}
}
2)dp的子问题相关,而分治的子问题是独立的:如0-1背包问题里P(n-2,c-v)同时在子问题P(n-1,c-v)和P(n-1,c)的求解过程中出现,子问题具有重叠性。

