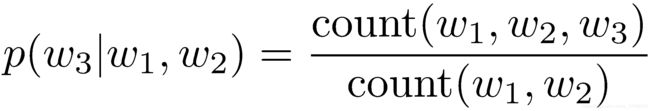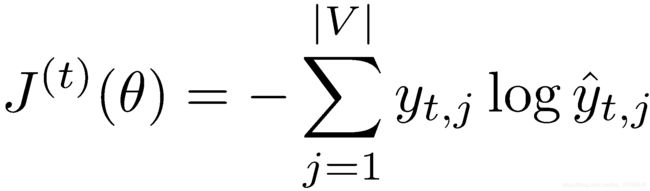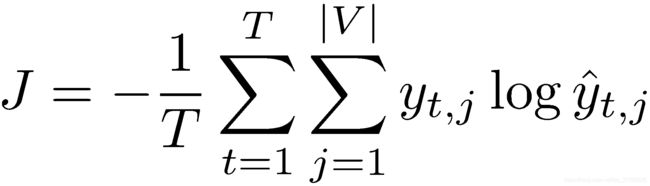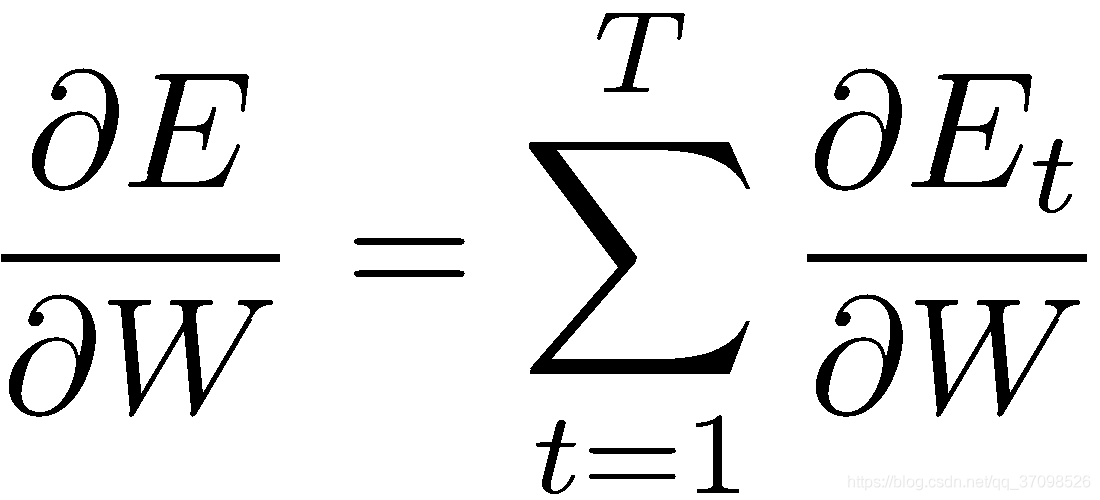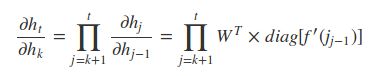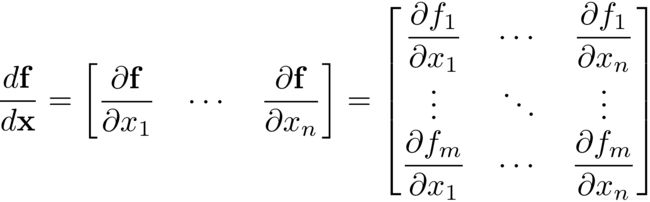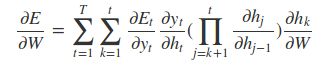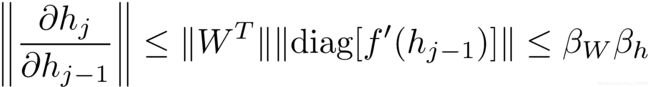CS224N笔记——RNN和语言模型
目录
传统语言模型
循环神经网络语言模型
损失函数
训练RNN时的困难
梯度消失问题
梯度消失实例
防止梯度爆炸
减缓梯度消失
困惑度结果
问题：softmax太大且太慢
一个实现技巧
序列模型的应用
双向和深层RNNs
双向RNNs
深层双向RNNs
评测
-
传统语言模型
语言模型就是计算一个单词序列（句子）的概率
的模型。可以用于机器翻译中，判断译文序列中一种词序的自然程度高于另一种，判断一种用词选择优于另一种。
为了简化问题，引入马尔科夫假设，句子的概率通常是通过待预测单词之前长度为n的窗口建立条件概率来预测：
为了估计此条件概率，常用极大似然估计，比如对于Bigram和Trigram模型，有：
在数据量足够的情况下，n-gram中的n越大，模型效果越好。但实际上，数据量总是不如人意，这时候一些平滑方法就不可或缺。另外，这些ngram可能会占用上G的内存，在最新的研究中，一个1260亿的语料在140G内存的单机上花了2.8天才得到结果。
-
循环神经网络语言模型
新的语言模型是利用RNN对序列建模，复用不同时刻的线性非线性单元及权值，理论上之前所有的单词都会影响到预测单词。
所需内存只与词表大小成正比，不取决于序列长度。
给定一个词向量序列：
，在每个时间点上都有隐藏层的特征表示：
损失函数
分类问题中常见的交叉熵损失函数：
在大小为T的整个语料上的交叉熵误差为：
如果以2为底数会得到“perplexity困惑度”，代表模型下结论时的困惑程度，越小越好：
Perplexity：
-
训练RNN时的困难
观察句子1：
"Jane walked into the room. John walked in too. Jane said hi to ___"
以及句子2：
"Jane walked into the room. John walked in too. It was late in the day, and everyone was walking home after a long day at work. Jane said hi to ___"
人类可以轻松地在两个空中填入“John”这个答案，但RNN却很难做对第二个。这是因为在前向传播的时候，前面的x
反复乘上W，导致对后面的影响很小。
反向传播时也是如此。
梯度消失问题
整个序列的预测误差是之前每个时刻的误差之和：
而每个时刻t的误差又是之前每个时刻的误差之和，应用链式法则：
此处的
指的是在[k,t]时间区域上应用链式法则：
由于
，每个
就是h的雅克比矩阵（导数矩阵）：
将这几个式子写在一起，得到：
这个式子最中间的部分最值得关注，因为它是一个连乘的形式，长度为时间区域的长度。记βW 和 βh分别为矩阵和向量的范数(L2)，则上述雅克比矩阵的范数满足：
指数项
在
显著地大于或小于1的时候，经过足够多的t−k次乘法之后就会趋近于0或无穷大。小于1更常见，会导致很长时间之前的词语无法影响对当前词语的预测。
而大于1时，浮点数运算会产生溢出（NaN），一般可以很快发现。这叫做梯度爆炸。小于1，或者下溢出并不产生异常，难以发现，但会显著降低模型对较远单词的记忆效果，这叫做梯度消失。
梯度消失实例
http://cs224d.stanford.edu/notebooks/vanishing_grad_example.html
防止梯度爆炸
一种暴力的方法是，当梯度的长度大于某个阈值的时候，将其缩放到某个阈值。虽然在数学上非常丑陋，但实践效果挺好。
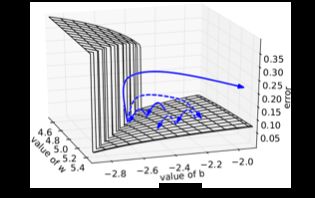
其直观解释是，在一个只有一个隐藏节点的网络中，损失函数和权值w偏置b构成error surface，其中有一堵墙：
每次迭代梯度本来是正常的，一次一小步，但遇到这堵墙之后突然梯度爆炸到非常大，可能指向一个莫名其妙的地方（实线长箭头）。但缩放之后，能够把这种误导控制在可接受的范围内（虚线短箭头）。
但这种trick无法推广到梯度消失，因为你不想设置一个最低值硬性规定之前的单词都相同重要地影响当前单词。
减缓梯度消失
与其随机初始化参数矩阵，不如初始化为单位矩阵。这样初始效果就是上下文向量和词向量的平均。然后用ReLU激活函数。这样可以在step多了之后，依然使得模型可训练。
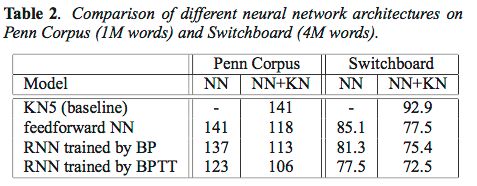
困惑度结果
相较于NGram，RNN的困惑度要小一些。
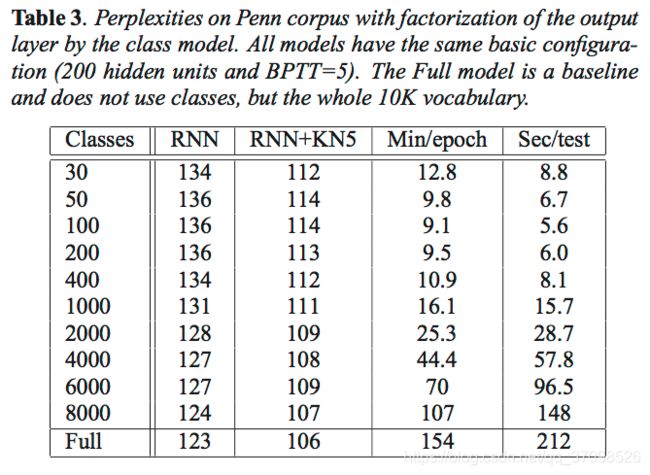
问题：softmax太大且太慢
词表太大的话，softmax很费力。一个技巧是，先预测词语的分类（比如按词频分），然后在分类中预测词语。分类越多，困惑度越小，但速度越慢。所以存在一个平衡点：
一个实现技巧
记录每个t的误差不要丢，反向传播的时候将其累加起来。
-
序列模型的应用
可以把每个词分类到NER、实体级别的情感分析、意见表达。
其中，意见挖掘任务就是将每个词语归类为：
DSE：直接主观描述（明确表达观点等）
ESE：间接主观描述（间接地表达情感等）
语料标注采用经典的BIO标注：
实现这个任务的朴素网络结构就是一个裸的RNN：
但是这个网络无法利用当前词语的下文辅助分类决策，解决方法是使用一些更复杂的RNN变种。
-
双向和深层RNNs
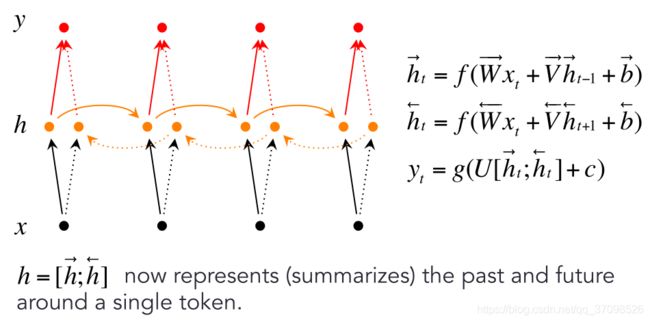
双向RNNs
这里箭头表示从左到右或从右到左前向传播，对于每个时刻t的预测，都需要来自双向的特征向量，拼接后进行分类。箭头虽然不同，但参数还是同一套参数（有些地方是两套参数）。
深层双向RNNs
理解了上图之后，再加几个层，每个时刻不但接受上个时刻的特征向量，还接受来自下层的特征表示：
评测
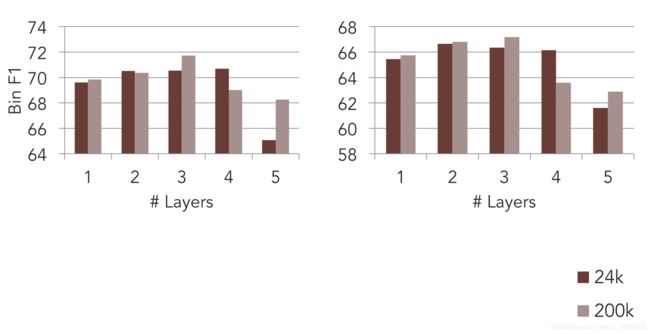
评测方法是标准的F1（因为标签样本不均衡），在不同规模的语料上试验不同层数的影响：
可见层数不是越多越好。