卷积神经网络初体验
因为最近看论文 发现经常出现卷积神经网络的相关内容,迫于压力,这一期博客的主要内容就是和大家一起学习深度学习中最著名的卷积运算和卷积神经网络的相关内容,由于代码水平实在是有限,所以这里主要是理论和解释为主,之后代码也会及时更新!
Convolutional Neural Networks
- 一 . 卷积运算
- 二 . 卷积神经网络
- 1. 数据预处理
- 2. 卷积计算层
- 3. 激励层
- 4. 池化层
- 5. 全连接层
卷积网络(convolutional network)(LeCun, 1989),也叫做卷积神经网络(con-volutional neural network, CNN),是一种专门用来处理具有类似网格结构的数据的神经网络。例如时间序列数据(可以认为是在时间轴上有规律地采样形成的一维网格)和图像数据(可以看作是二维的像素网格)。卷积网络在诸多应用领域都表现优异。“卷积神经网络’’ 一词表明该网络使用了卷积(convolution)这种数学运算。卷积是一种特殊的线性运算!

用大佬的图片镇楼,此人便是创造 CNN 的著名计算机科学家 Yann LeCun ,目前在Facebook 中工作!
一 . 卷积运算
在真正深入了解之前,我们还是先来看一下什么是卷积,如何进行运算?
我们这里需要进行一个实验:一个小球从某一高度做自由落体,等到这个小球平静之后 在原来的位置再做一次自由落体,当然这些小球,可以在这两层平面上呈现一维的滑动,就像这样:
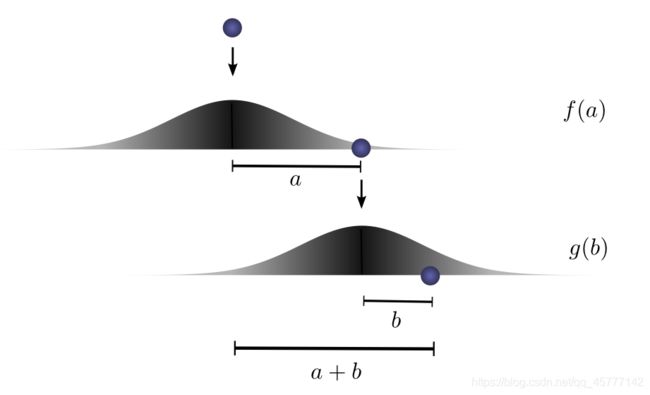
第一次下落后滑动了距离释放点水平距离为 a a a 的概率函数为 f ( a ) f(a) f(a) ,那么同理,我们在第一次下落静止后,将小球再做一次自由落体,那么滑动距离为 b b b 的概率函数为 g ( b ) g(b) g(b) ;那么我们结合这两次的实验操作,总共滑动的距离 c = a + b c =a+b c=a+b 的概率函数为 : f ( a ) g ( b ) f(a)g(b) f(a)g(b) 这里有点像排列组合里面的那个分步相乘!
这是我们假设距离为 c c c 的一种理想实现,例如对于 c = 3 c=3 c=3来说: a = 1 , b = 2 a=1,b=2 a=1,b=2 是满足条件的,那么对于 a = 2 , b = 1 a=2,b=1 a=2,b=1 来说也是成立的:
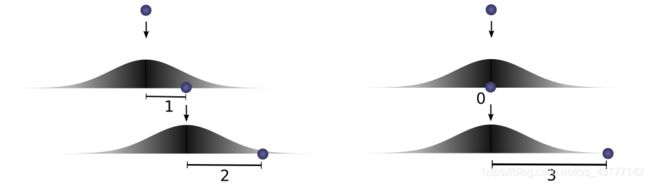
所以,对于 c = 3 c=3 c=3 这种情况下的总体概率,我们需要对所有可能的存在情况求和:
… f ( 0 ) ⋅ g ( 3 ) + f ( 1 ) ⋅ g ( 2 ) + f ( 2 ) ⋅ g ( 1 ) … \ldots f(0) \cdot g(3)+f(1) \cdot g(2)+f(2) \cdot g(1) \ldots …f(0)⋅g(3)+f(1)⋅g(2)+f(2)⋅g(1)…
了解这些之后我们就可以看一看卷积的定义了:
( f ∗ g ) ( c ) = ∑ a + b = c f ( a ) ⋅ g ( b ) (f * g)(c)=\sum_{a+b=c} f(a) \cdot g(b) (f∗g)(c)=a+b=c∑f(a)⋅g(b)
替换一下就可以得到:
( f ∗ g ) ( c ) = ∑ a f ( a ) ⋅ g ( c − a ) (f * g)(c)=\sum_{a} f(a) \cdot g(c-a) (f∗g)(c)=a∑f(a)⋅g(c−a)这种运算就叫做原始的一维标准卷积(convolution),卷积运算通常用星号表示!
为了更好的拟合这个式子,刚才说的小实验可以完善一下:
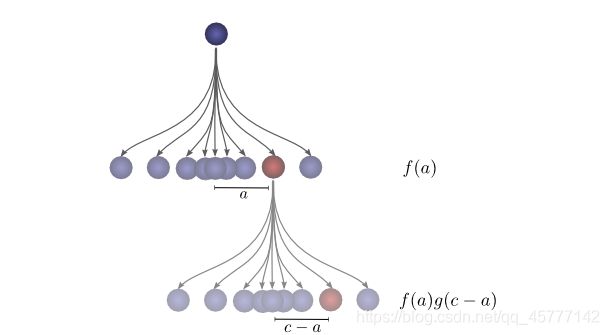
这样是不是就更直观了,对于所有的情况,可以看下面这张图片:
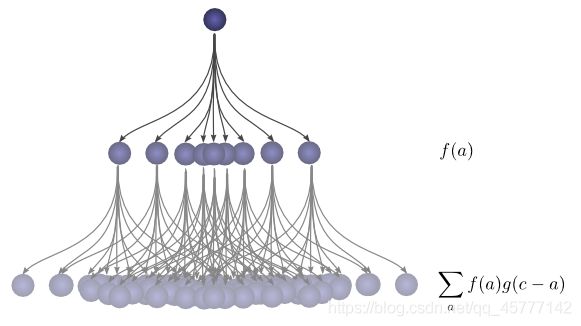
在卷积网络的术语中,卷积的第一个参数(在这个例子中就是函数 f f f,通常叫做输入 ( i n p u t ) (input) (input)),第二个参数(函数 g g g)叫做核函数(kernel function) ,输出有时被称作特征映射(feature map)。
那么回过头来,我们这里只是一个一维的卷积运算,高维的卷积才是计算机技术应用的主要战场,当然,我们也可以把上面的这个例子改成二维的:
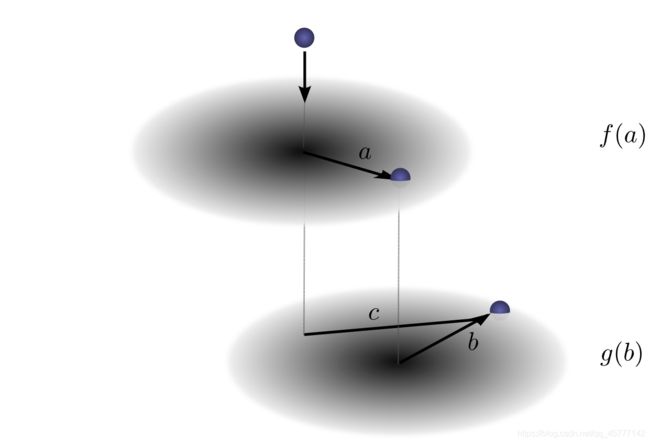
这里公式表达为:
( f ∗ g ) ( c 1 , c 2 ) = ∑ a 1 + b 1 = c 1 ; a 2 + b 2 = c 2 f ( a 1 , a 2 ) ⋅ g ( b 1 , b 2 ) (f * g)\left(c_{1}, c_{2}\right)=\sum_{a_{1}+b_{1}=c_{1} ; a_{2}+b_{2}=c_{2}} f\left(a_{1}, a_{2}\right) \cdot g\left(b_{1}, b_{2}\right) (f∗g)(c1,c2)=a1+b1=c1;a2+b2=c2∑f(a1,a2)⋅g(b1,b2)
和前面的原理基本上一模一样,这里的 a 1 , a 2 a_{1},a_{2} a1,a2 可以理解为上面两个平面中的坐标,坐标相加最终就能得到 c c c 了。
毫无疑问,你也可以写成这个样子:
( f ∗ g ) ( c 1 , c 2 ) = ∑ a 1 , a 2 f ( a 1 , a 2 ) ⋅ g ( c 1 − a 1 , c 2 − a 2 ) (f * g)\left(c_{1}, c_{2}\right)=\sum_{a_{1}, a_{2}} f\left(a_{1}, a_{2}\right) \cdot g\left(c_{1}-a_{1}, c_{2}-a_{2}\right) (f∗g)(c1,c2)=a1,a2∑f(a1,a2)⋅g(c1−a1,c2−a2)
目前为止,我们简单的理解了一下卷积的含义和运算,下面我们正式进入卷积神经网络的学习!
二 . 卷积神经网络
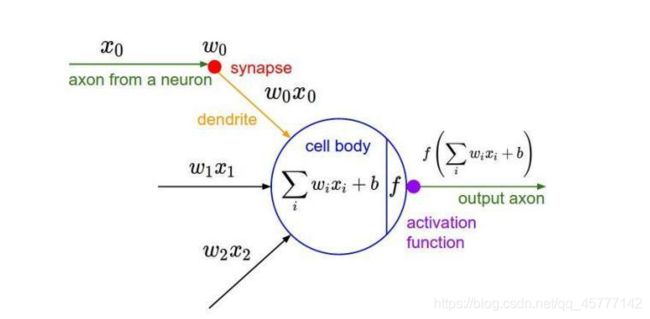
我们刚刚介绍了一下卷积的相关内容,现在再来看看神经网络:
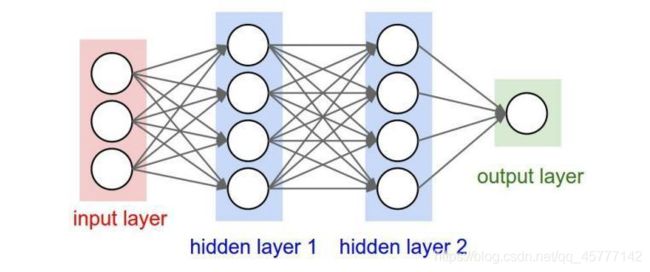
这个图片我相信 研究算法的小伙伴们就再熟悉不过了!输入层之后,建立多个隐藏层和隐藏神经元,大量的训练模拟之后输入结果!
其实卷积神经网络还是建立在深度学习的 神经网络上面的,只不过在其中的算法和步骤发生了些许的改变,比如说区分车的种类:

如上图所示,卷积神经网络架构与常规人工神经网络架构非常相似,特别是在网络的最后一层,即全连接。此外,还注意到卷积神经网络能够接受多个特征图作为输入,而不是向量!
卷积神经网络的层级结构 :
- 数据输入层(Input layer)
- 卷积计算层(CONV layer)
- ReLU激励层 (ReLU layer)
- 池化层 (Pooling layer)
- 全连接层 (FC layer)
1. 数据预处理
个人觉得不管是机器学习还是深度学习 ,数据预处理是必须的!在卷积神经网络中,我们一般有三种方式:
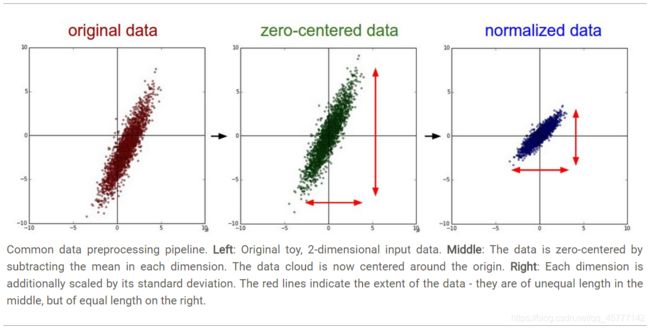
零均值:
顾名思义,就是将每一维原始数据减去每一维数据的平均值,将结果代替原始数据,这就是零均值。
归一化(normalization)
- 其中一种就是先将原始数据先进行零均值处理,再将每一维的数据除以每一维数据的标准差!
- 第二种就是将数据区间幅度归一化到同样的范围,如图所示:
归一化可以在每一个子集训练的时候让训练数据有相同的分布,加快模型收敛,如果每次数据分布不同,模型更新过程中会付出一定代价用来调整这种分布的差异,蝴蝶效应逐渐拉大误差!
PCA/白化:
用 P C A PCA PCA 算法先对数据降维;白化是对数据各个特征轴上的幅度归一化,这个在CNN里面不常用到 就不说了~~
2. 卷积计算层
这是卷积网络中的特色所在,也是最重要的一部分,我们需要深刻理解它:
我们可以大概的来看一下这张图片,它是一个(一般图片处理有多个)卷积层的基本流程,有些名词马上就会介绍:
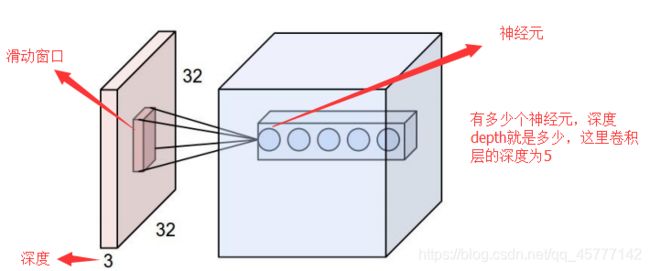
这个滑动的窗口会从左向右移动,有多少个神经元,就会有多少次卷积运算!比如我们想对一个图片处理,输入内容为一个 32 x 32 x 3 的像素值数组,你可以想象我有个正方形手电筒从这个图像的左上角照过,如果手电筒的光可以覆盖 5 x 5 的区域,想象一下手电筒光照过输入图像的所有区域,我们通常把这个手电筒被叫做过滤器(filter,有时候也被称为神经元(neuron)或核(kernel),也就是前面卷积计算中的核函数!),被照过的部分区域被称为感受野(receptive field) 。
过滤器同样也是一个数组(其中的数字被称作权重或参数),显然,过滤器的深度必须和我们输入原始数据的深度相同,因此过滤器大小为 5 x 5 x 3,按照上面图来说的话是这样的!
下面来看一下什么叫填充值 ?比如这有这么一个5 x 5的图片,我们的滑动窗口取2x2,步长取2,那么我们发现还剩下1个像素没法滑完,那怎么办呢?
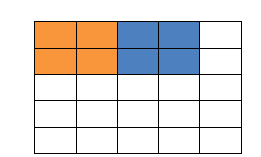
这里我们在原先的矩阵加了一层填充值,使得变成6x6的矩阵,那么窗口就可以刚好把所有像素遍历完。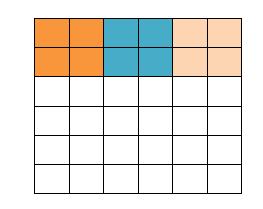
那,这也算是在卷积之前对图像的一个预处理过程!接下来的过程就是核心了:
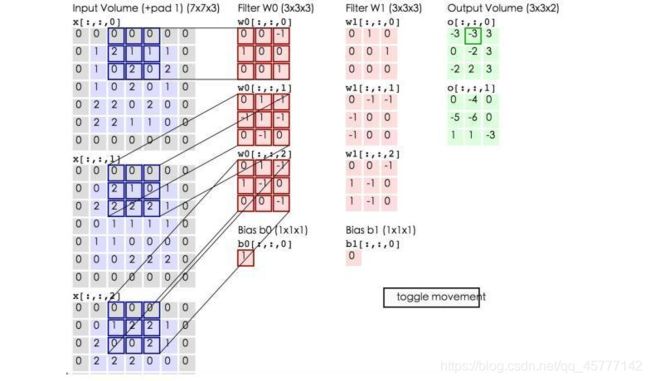
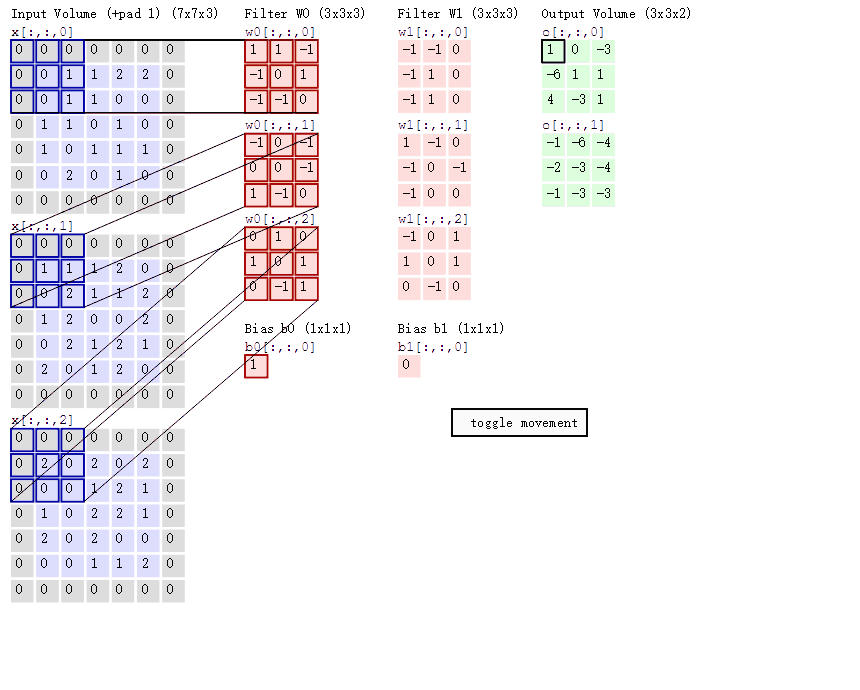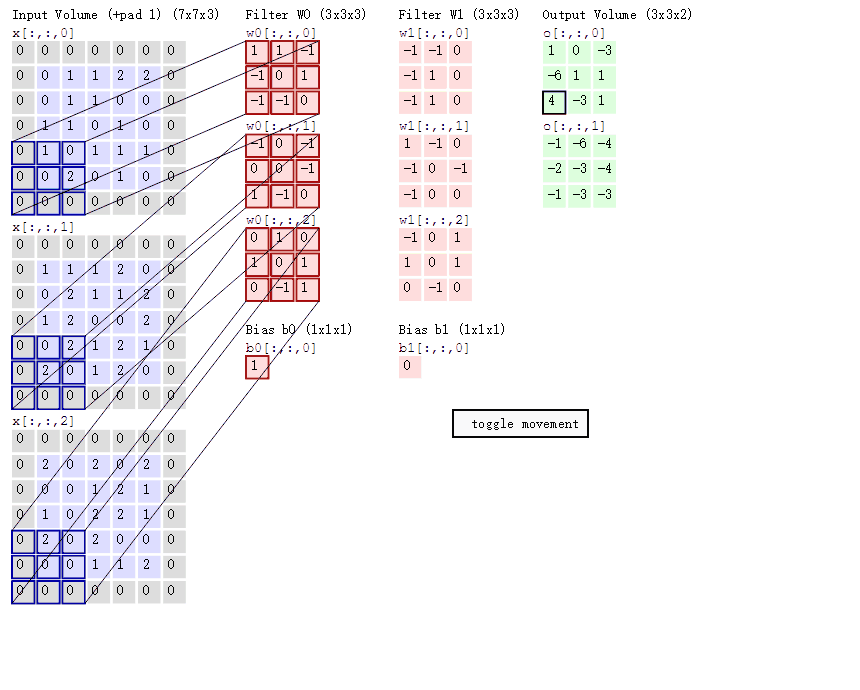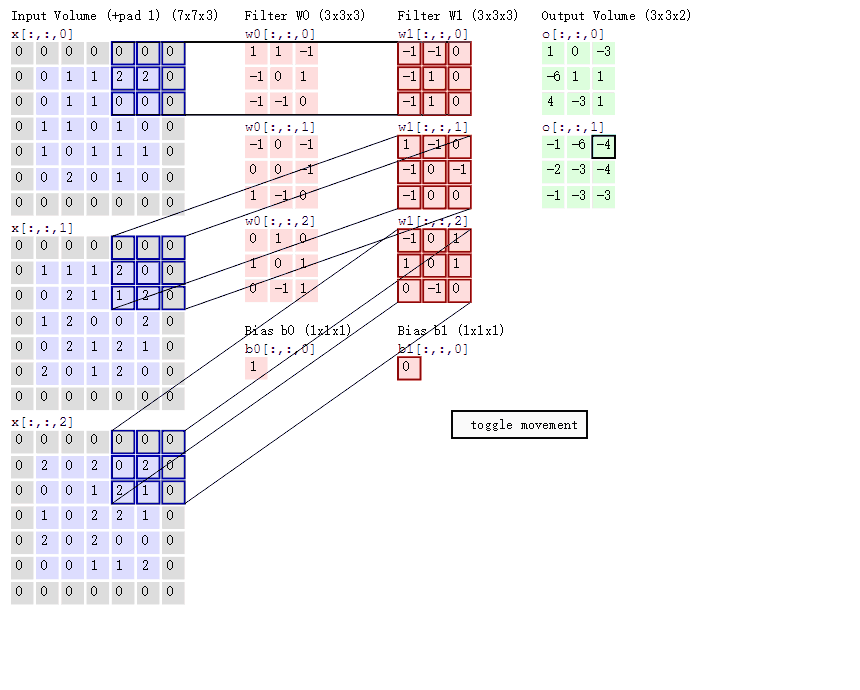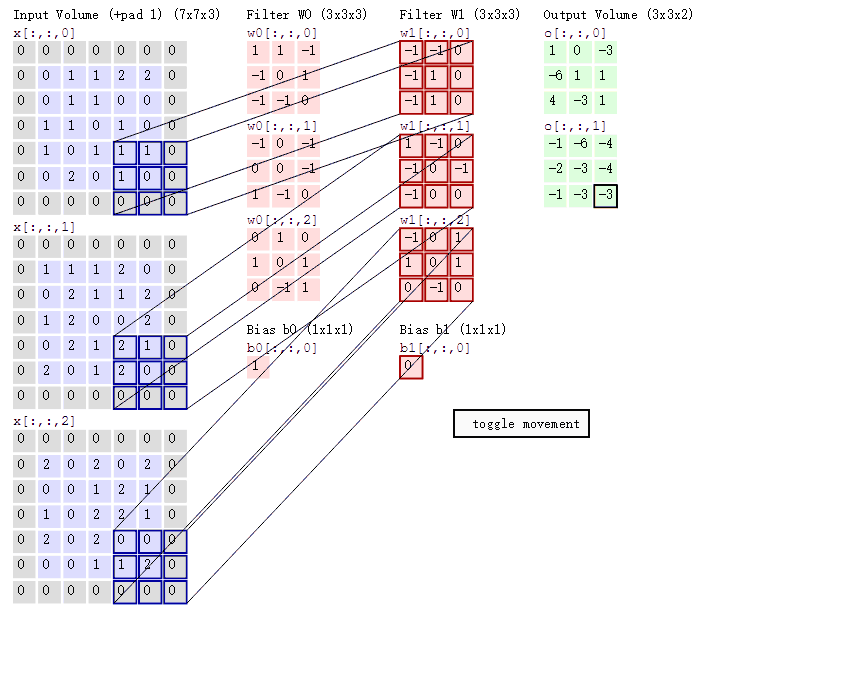
蓝色矩阵就是输入的元素图像数据,灰色部分就是填充值,粉色矩阵就是卷积层的过滤器,这里表示了有两个过滤器(w0,w1),也就是两个神经元。绿色矩阵就是经过卷积运算后的输出矩阵,这里的步长设置为2!
因为这里的图像是一个三阶张量 深度为3 ,取n模之后 我们会得到三个矩阵,这也是RGB 图像格式的 常用处理方式,后面会说的,这里我们只需要理解它是怎么卷积的就行了!
蓝色的矩阵(输入图像)对粉色的矩阵(filter)进行矩阵内积计算并将三个内积运算的结果与偏置值 b b b 相加(比如上面图的计算:2+(-2+1-2)+(1-2-2) + 1= 2 - 3 - 3 + 1 = -3),计算后的值就是绿框矩阵的一个元素!
这里的动态图片非常的清晰展示了计算的流程!
所以 你明显发现了,数据的维数降低了,所以卷积也叫做 “降维打击” !
当然,如果我们改变过滤器器的大小 ,或者是步长,得到的新矩阵维数也就发生变化了,得到的新矩阵也包含了原始数据的特征,甚至我们可以不改变原来图片矩阵的维数,下面两张图片就是对于不同的步长,卷积得到的不同结果,第二个甚增加的填充层之后使得新矩阵没有发生维数的改变:
步长为2:
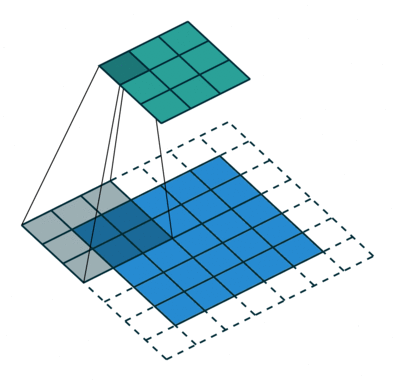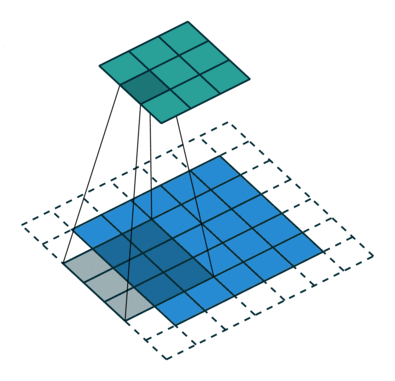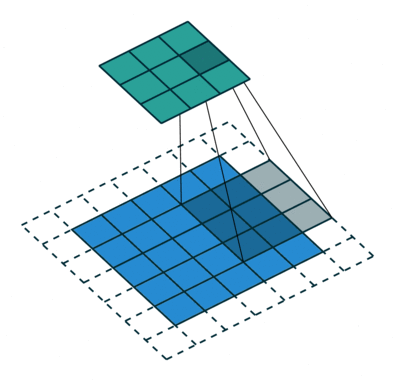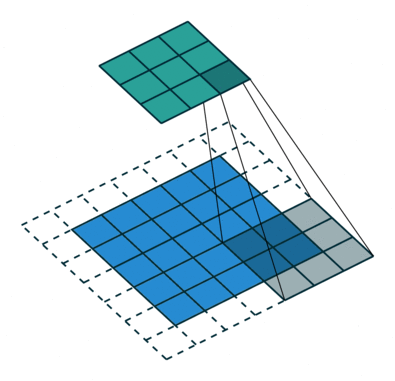
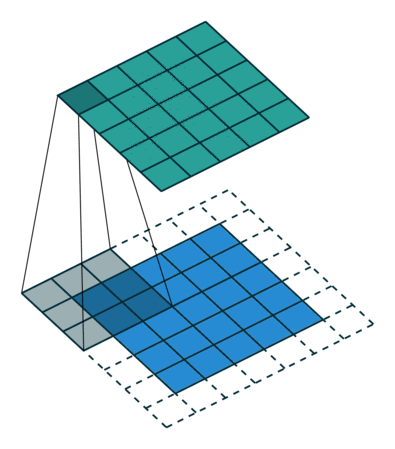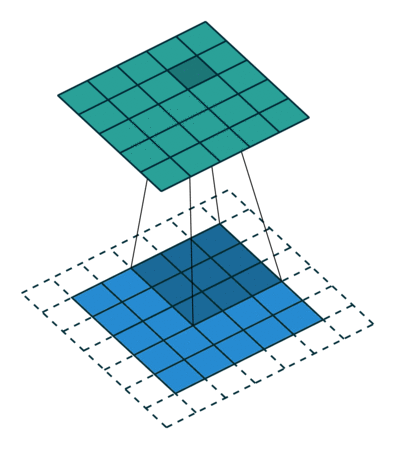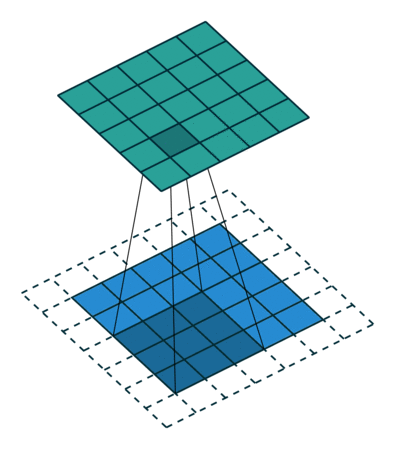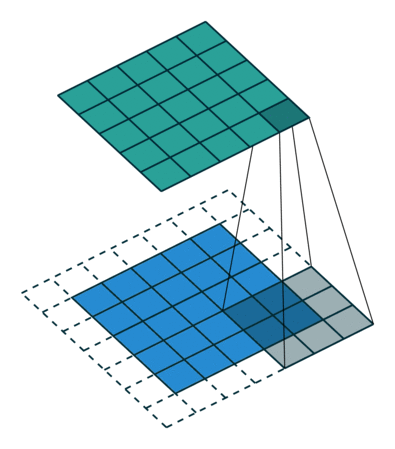
甚至,我们可以改变填充值的数量能够达到不降维反升维的过程!
我们的CNN(convolutional neural network),主要就是通过一个个的filter,不断地提取特征,从局部的特征到总体的特征,从而进行图像识别等等功能
那么我们现在回过头来,看看我们引入填充层的目的除了让我们配合步长进行卷积计算之外,还有什么作用呢?
看了上面的两幅图片,这个问题就简单了,如果我们设置多个卷积层,多次提取图片特征,那们新得到的数据维度会越来越小,最后就没了,但是减少卷积层的个数又达不到我们想要的效果,所以在原始数据中增加填充层也会的后面多次的卷积层运算 提供了便利!
除此之外,我们过滤器中的数据怎么来呢?
其实学过神经网络之后,你就就知道,这些 f i l t e r s filters filters,根本就不用我们去设计,每个 f i l t e r s filters filters中的各个数字,不就是参数吗,我们可以通过大量的数据,来 让机器自己去“学习”这些参数嘛。这,就是CNN的原理!
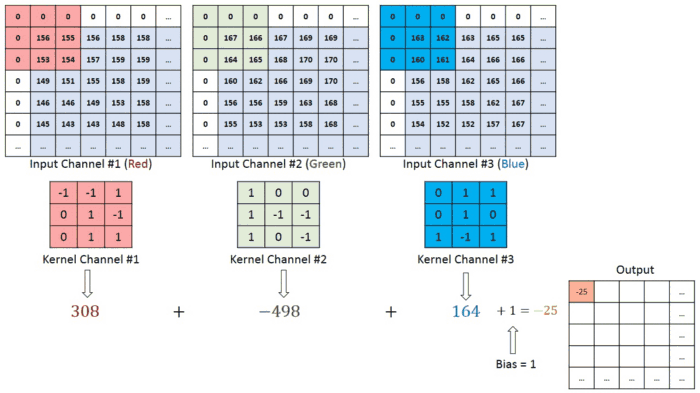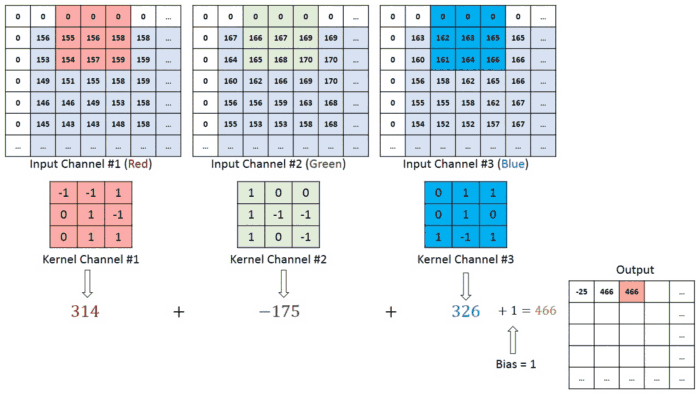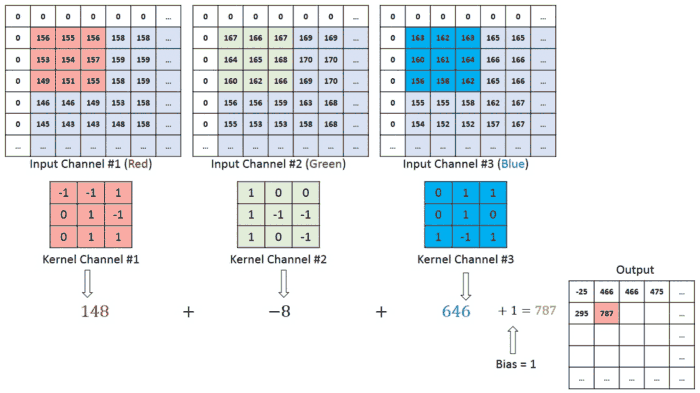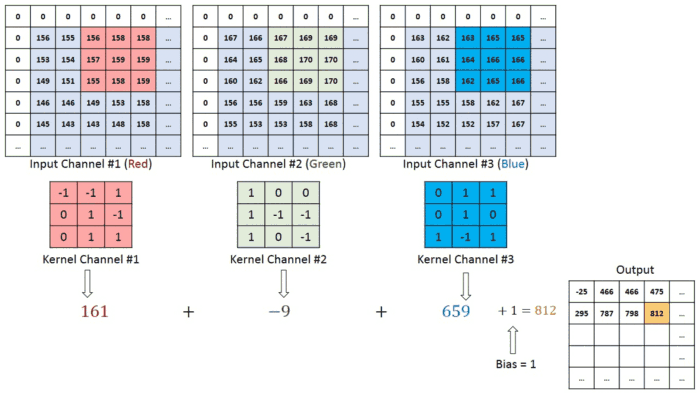
其实,对于单通道(灰度)图像来说,深度为1 ,非常简单,但是彩色图像一般都是采取 R G B RGB RGB 格式 的深度为3 的多通道图像,其实这与最上面的 那两幅图原理是一样的,这里的两张动态图片也是非常的清晰好懂:
这是我们起始是输入的图像数据,曲线的方向也就是过滤器的移动方向!
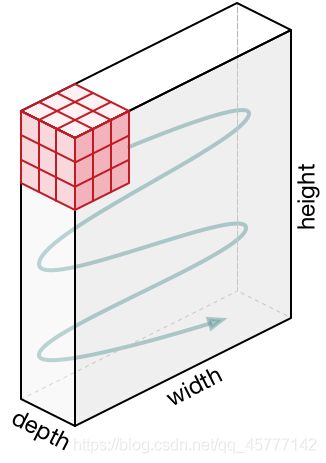
这就是对于红绿蓝三基色图片的 每层像素图片的卷积过程!
3. 激励层
在每个卷积层之后,立即应用一个非线性层(或激活层),其目的是给一个在卷积层中刚经过线性计算操作的系统引入非线性特征。因为神经网络能够在准确度不发生明显改变的情况下把训练速度提高很多。它同样能帮助减轻梯度消失的问题——由于梯度以指数方式在层中消失,导致网络较底层的训练速度非常慢。这一层把所有的负激活(negative activation)都变为零。这一层会增加模型乃至整个神经网络的非线性特征,而且不会影响卷积层的感受野!
4. 池化层
这个层级的位置就与众不同,它是夹在每个卷积计算层的中间,用于提取一定区域的主要特征,并减少参数数量,防止模型过拟合!如果输入是图像的话,那么池化层的最主要作用就是压缩图像!
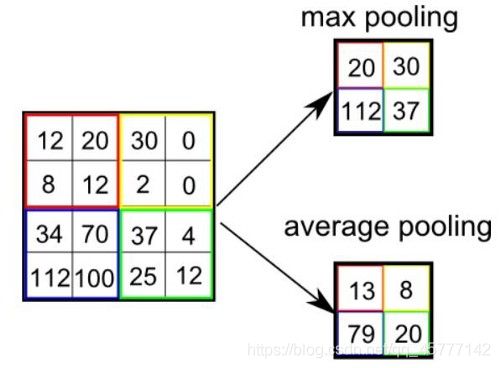
其中程序员最喜欢的就是最大池化法,它基本上采用了上述卷积层的过滤器和相应的步长,然后把它应用到输入内容上,输出过滤器卷积计算的每个子区域中的最大数字,就像下图这样:
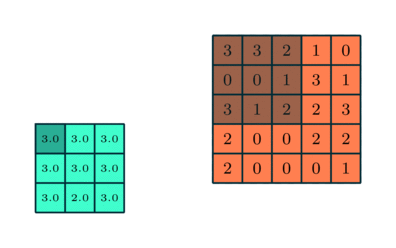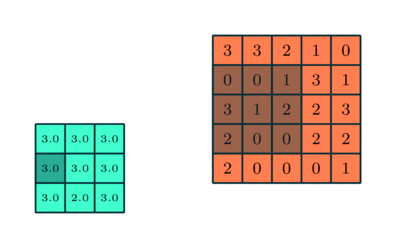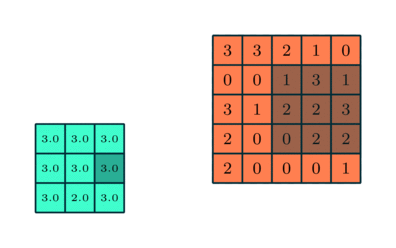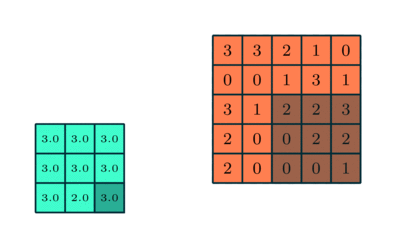
除此之外,常用的还有平均池化法,也就是取对应矩阵中元素的平均值,一般来说,最大池化也可以作为一个噪声抑制的方法,它抛弃了所有的噪声激活,也执行去噪和降维另一方面,平均池只是简单地执行降维作为一种噪声抑制机制。因此,从这个角度上来说 :最大池化的性能比平均池化要好得多,下图展示了两种池化法:
5. 全连接层
这里就和神经网络中的全连接层 一样了,没有啥特色。因为这一层是每一个单元都和前一层的每一个单元相连接,所以称之为“全连接”。这里要指定的超参数,无非就是神经元的数量,以及激活函数!
现在我们已经将输入图像转换为多层感知器的恰当形式,接下来我们将把图像扁平化为列向量。将平滑的输出反馈给前神经网络,反向传播应用于训练的每次迭代。该模型能够在一定时期内区分图像中的主要特征和某些低层次特征,并采用Softmax分类技术对其进行分类!博客开头的汽车分类图片类似于这样!
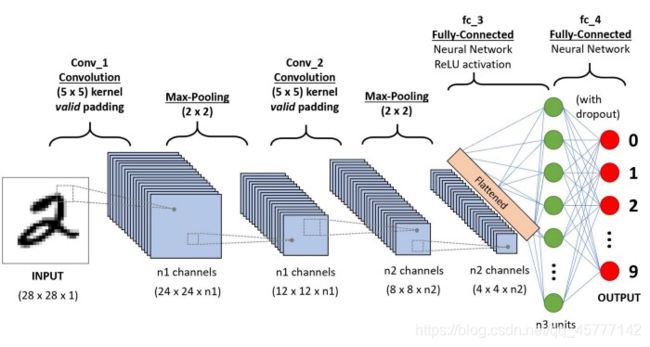
这就是我们整个卷积神经网络的一个过程,大家可以按照这个流程在脑海中回顾一下!
本期博客就是这些,希望大佬们多多点赞,多多评论!