无向图的广度优先遍历

描述

    前一篇博客讲了无向图的深度优先遍历

    使用广度优先遍历前一篇博客的图结果如下

   这五个顶点的被访问顺序如下

思路

    首先以一个未被访问过的顶点作为起始项点，访问其所有相邻的顶点，然后对每个相邻的顶点，在访问它们相邻的未被访问过得顶点，直到所有顶点都被访问过，遍历结束

    例如对上图的遍历过程

    从顶点 1 开始，依次访问 1 相邻的顶点 2 3 5。

然后再以下一个顶点 2 开始访问它相邻的顶点 4 。以此类推。

源代码

#define _CRT_SECURE_NO_WARNINGS 1

#include 
#include 

/*
* 使用广度优先遍历遍历无向图
* 郭文峰
* 2018/10/17
*/

int main(void)
{
	int i = 0;
	int j = 0;
	int n = 0;
	int m = 0;
	int a = 0;
	int b = 0;
	int cur = 0;
	int book[101] = { 0 };
	int e[101][101] = { 0 };
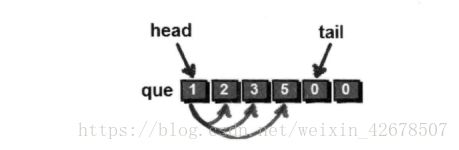
	int que[10001] = { 0 };
	int head = 1;
	int tail = 1;

	scanf("%d%d", &n, &m);

	for (i = 1; i <= n; i++)
	{
		for (j = 1; j <= n; j++)
		{
			if (i == j)
			{
				e[i][j] = 0;//使i == j 的点也就是自己访问自己的点等于0
			}
			else
			{
				e[i][j] = 999999; //先默认所有的点都不能互相访问，并认为999999为正无穷
			}
		}
	}

	for (i = 1; i <= m; i++)
	{
		scanf("%d%d", &a, &b);
		e[a][b] = 1;
		e[b][a] = 1;

	}

	//先将1结点入栈
	que[tail] = 1;
	tail++;
	book[1] = 1;

	while (head < tail)
	{
		cur = que[head];

		for (i = 1; i <= n; i++)
		{
			if (e[cur][i] == 1 && book[i] == 0)
			{
				que[tail] = i;
				tail++;
				book[i] = 1;
			}

			if (tail > n)
			{
				break;
			}
		}

		head++;
	}

	for (i = 1; i < tail; i++)
	{
		printf("%d ", que[i]);
	}

	system("pause");
	return 0;

}