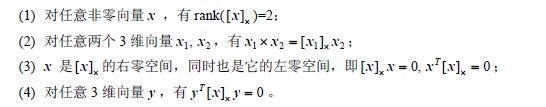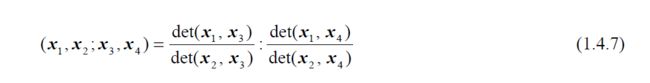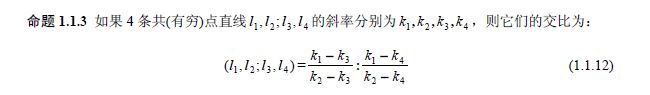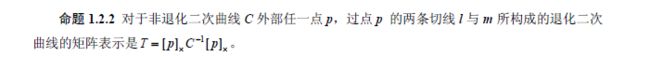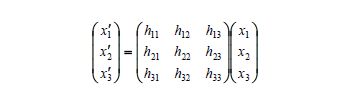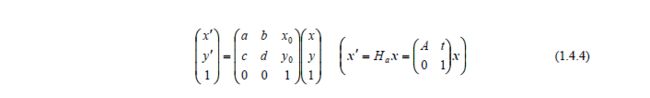平面与空间射影几何小结——平面射影几何
好像两三天没更新了,在看矩阵论耽误了一下。。。
在后续章节学习中帮助快速查询相关知识
平面与空间射影几何小结——平面射影几何
- 零散内容
- 射影平面
- 三维向量的叉积运算
- 叉积的反对称矩阵表示
- 射影平面内的点线关系
- 对偶原理
- 射影平面上过两点的直线上的点的表示
- 过射影平面上两点的直线表示
- 射影平面上三点共线的充要条件
- 平面两线交点
- 平面三线共点充要条件
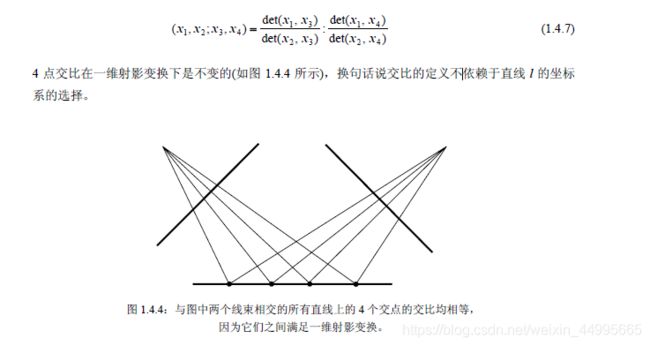
- 交比相关
- 射影平面的共线点、共点线的
- 共线点
- 共线点参数化表示
- 共线点的交比
- 调和共轭
- 有限点的交比简化
- 直线上有限点与其无穷远点的交比
- 共点线
- 共点线参数化表示
- 共点线的交比
- 根据斜率计算共点线的交比
- 共点线与共线点的关系
- 二次曲线、二次曲面等
- 射影平面中的二次曲线
- 二次曲线矩阵表示
- 退化的二次曲线
- 二次曲线上的点:切点与切线
- 二次曲线外的点:切点与切线
- 配极对应变换
- 配极对应
- 共轭点
- 自极三角形
- ?注意点Z在C内部的情况?
- 射影平面中的对偶二次曲线
- 非退化情况
- 退化情况
- 圆环点及其对偶
- 圆环点(所有圆与无穷远线的交点)
- 圆环点的对偶(对偶二次曲线)
- 两条非迷向直线的交角
- 拉格尔(Laguerre)定理(交比与夹角的关系)
- 二维射影变换
- 二维射影变换
- 射影变换
- 四点确定二维射影变换
- 直线与二次曲线的射影变换
- 直线在射影变换H 下变换规则
- 二次曲线在射影变换H 下变换规则
- 二次曲线的射影分类
- 变换群与不变量
- 等距变换群
- 欧氏变换群
- 欧氏不变量
- 相似变换群
- 相似不变量
- 仿射变换群
- 仿射变换的分解
- SVD分解
- QR分解
- 仿射不变量
- 二次曲线的仿射分类
- 射影变换群
- 射影不变量
零散内容
射影平面
由欧氏平面与无穷远直线的并集所形成的扩展平面称为射影平面,有时也称为二维射影空间。
直线l = (a, b, c)T交无穷远线于l = (-b, a, 0)T,这也是直线的方向,(a, b, 0)T为法线方向。
三维向量的叉积运算
叉积的反对称矩阵表示
射影平面内的点线关系
对偶原理
在射影平面内,点和线是一对互为对偶元素。在包含“点”和“线”元素的命题中,如果将两个元素的角色互换,则对应的命题也成立,并称它们是一对互为对偶命题。
射影平面上过两点的直线上的点的表示
对直线 l上的任一点,它的齐次坐标可以表示为![]()
过射影平面上两点的直线表示
射影平面上三点共线的充要条件
平面两线交点
平面三线共点充要条件
![]()
交比相关
射影平面的共线点、共点线的
共线点
共线点参数化表示

![]()
这种参数化过程实际上是建立直线坐标系的过程。直线上点的参数化不是唯一的,不同的参数化对应不同的坐标系。
共线点的交比
共线点的交比不依赖于点参数化的选择,或者说不依赖于直线坐标系的选择。

根据交比不依赖于参数化选择的性质,可以简化交比的计算。

调和共轭
有限点的交比简化
直线上有限点与其无穷远点的交比
共点线
共点线参数化表示
共点线的交比
根据斜率计算共点线的交比
共点线与共线点的关系
二次曲线、二次曲面等
射影平面中的二次曲线
二次曲线矩阵表示
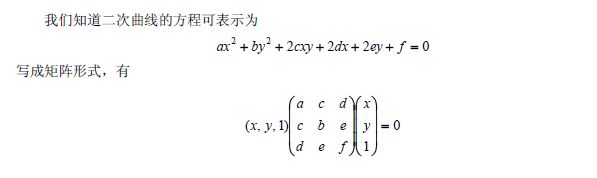
即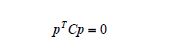 矩阵C是二次曲线的矩阵表示。
矩阵C是二次曲线的矩阵表示。
二次曲线C 有5 个自由度。在一般情况下,射影平面上的5个点唯一确定一条二次曲线,并由上述方程解得矩阵C。
退化的二次曲线
二次曲线根据它的秩(即C 的秩)是否是满秩分为非退化与退化的两种情况。非退化二次曲线是正常二次曲线,退化二次曲线或者是由两条直线所构成(rankC=2),或者由二条重合直线所构成(rankC=1)。
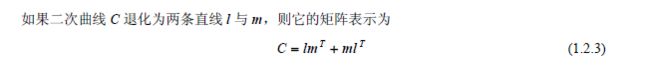
二次曲线上的点:切点与切线
求切点处的切线表示
求切线与二次曲线的交点
判断l是不是二次曲线C的切线

该命题对退化二次曲线仍成立。
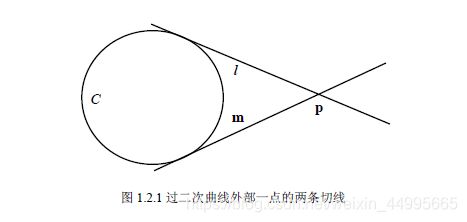
二次曲线外的点:切点与切线
配极对应变换
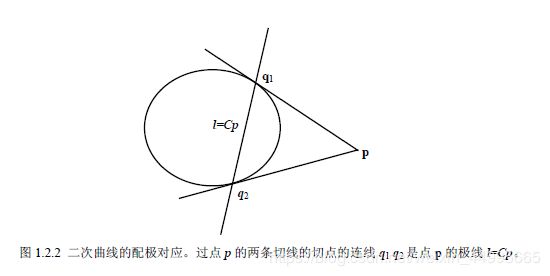
配极对应
给定一条二次曲线C,则对平面上的任一点p,l=Cp 确定了一条直线。
极点:直线l 称为点p 关于C的极线,而点p 称为直线l 关于C 的极点。
极线:如果点p 在C 上,则它关于C 的极线是通过它的切线l,而切线l 关于C 的极点是切点p。
由二次曲线所确定的这种点与直线之间的对应关系称为二次曲线的配极对应。
点p 关于非退化二次曲线C 的极线l=Cp 交C 于两个点,且C 在这两个交点的切线交于点p。
共轭点
如果两个点p, q使得 pTCq = 0,则称点p, q 关于 C互为共轭。
不难看出点p 关于 C的所有共轭点所构成的集合是点p 关于C 的极线。
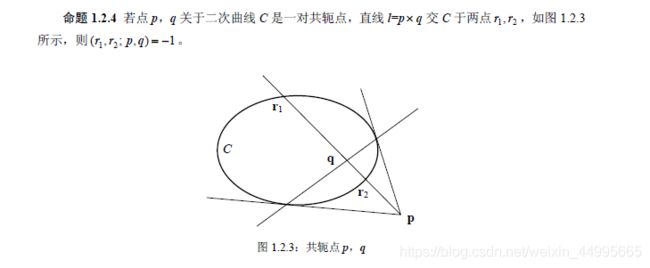
自极三角形
如果一个三角形的三个顶点都是其对边关于二次曲线C 的极点,则称它为C 的自极三角形。
例如:二次曲线上的四点构成的完全四点形的对边三角形是该二次曲线的自极三角形。
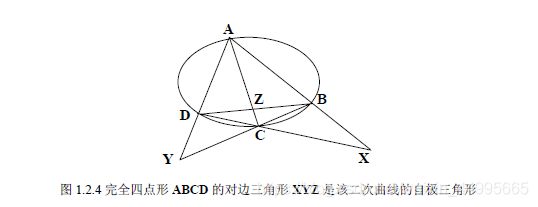
?注意点Z在C内部的情况?
射影平面中的对偶二次曲线
由直线生成的二次曲线通常称为对偶二次曲线。在几何上,对偶二次曲线是直线族的包络,即C*的几何元素是二次曲线的切线。
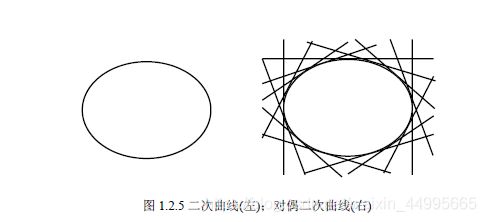
线元素的二次方程:
![]()
非退化情况
退化情况

对偶退化二次曲线只有两个点。(个人:分别取自直线l与m上的点,从而满足线元素的二次方程)
圆环点及其对偶
圆环点(所有圆与无穷远线的交点)
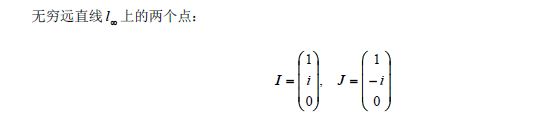
圆环点的方程可以表示为
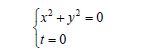
因此,圆环点可以看作是平面上的一条(退化)二次曲线。但必须限制t=0。
(在平面上,圆环点必须用两个方程来表示。如果限制在无穷远直线上,即,论域是无穷远直线而不是整个平面,则圆环点可由单个方程:x2 + y2 = 0来表达,它的矩阵表示是一个2阶单位矩阵。)

交点的齐次坐标必为I,J。现在,也可以解释为什么给定三个点能唯一确定一个圆,因为圆总是通过两个圆环点。所以,3 点确定一个圆与5 个点才能确定一条二次曲线并不矛盾,因为已经确定了两个点了。
圆环点的对偶(对偶二次曲线)
两条非迷向直线的交角
- 过平面内任意一点至两圆环点的两条直线,称为该点的迷向直线(极小直线)。
- 平面上,一条直线以及平行于这条直线的全体直线的集合叫做平行直线束。
- 迷向直线不象通常直线那样具有方向。
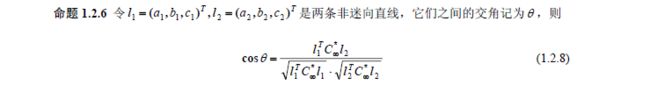
如果两条直线中有一条是迷向直线(或两条都是迷向直线),则它们之间的夹角是不定的。


拉格尔(Laguerre)定理(交比与夹角的关系)
两直线交点与两圆环点确定两条迷向直线,然后作为共点线计算交比。


这个定理用交比射影概念表达了角度量概念,形成了角度的射影解释,从而将欧氏几何与射影几何联系起来。

二维射影变换
二维射影变换
射影变换
- 在相同的线性空间相同的基下进行的线性变换。
- 由于变换是齐次的(点使用了齐次坐标),所以同一个射影变换矩阵H 可以相差一个非零常数因子,因此射影变换仅有8个自由度,即射影变换矩阵可由它的元素所构成的8 个比值所确定。
- 任何射影变换都将点变换到点,并且保持点的共线性质,因而将直线变为直线。
- 任何射影变换的逆变换(对应于单应矩阵的逆)都是射影变换、任意两个的合成(对应于两个单应矩阵的积)也都是射影变换,因此射影变换的全体构成射影平面上的一个变换群。
四点确定二维射影变换
直线与二次曲线的射影变换
直线在射影变换H 下变换规则
二次曲线在射影变换H 下变换规则
设 D 是一个可逆矩阵,则称矩阵变换 Y = DXDT 为合同变换。

二次曲线的射影分类

这里会问对diag(e1s1,e2s2,e3s3)再进行一次射影变换得到diag(s1.s2.s3)。
变换群与不变量
等距变换群

正交变换U根据它的行列式是否等于1而分为旋转变换与反射变换。当det(U) =1时,是旋转变换;det(U) = −1时,是反射变换。
它们的几何意义是旋转变换不但保持两点的距离不变,而且还保持方向(保向)不变。
欧氏变换群
旋转和平移的复合,好像和等距一样。
旋转矩阵:RTR=RRT=I的正交矩阵。
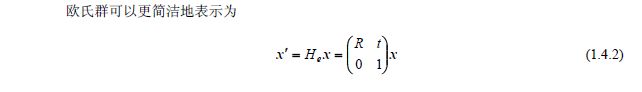
- 欧氏变换群是距变换群的子群(矩阵U 为反射的等距变换)。
- 平面欧氏变换有3 个自由度(因为在平面上,旋转有1 个自由度,平移有2 个自由度)。因此,两个点对应可确定欧氏变换。
欧氏不变量
两点的距离、两线的夹角、图形的面积等。由于欧氏群是等距变换群的子群,因此等距变换群的不变量也是欧氏不变量。
![]()
无穷远直线不变——并不是点点不变的,而是整个集合不变。
相似变换群


旋转相似变换有4 个自由度,因为它比欧氏变换多一个均匀伸缩因子。与欧氏变换一样,两个点对应也可以确定相似变换。
旋转相似变换是相似变换群的子群,而欧氏群又是旋转相似变换群的子群。
相似不变量
仿射变换群
- A 是一个2 阶可逆矩阵。
- 仿射变换有6 个自由度,3 个不共线的点对应唯一确定仿射变换。
- 仿射变换的全体也构成一个变换群,称为仿射变换群。相似变换群是它的子群。
- 仿射变换是否保向,根据矩阵A 的行列式det(A)是否大于零来确定。
- 所有保向仿射变换构成仿射变换群的子群,而旋转(保向)相似变换群又是它的子群。
仿射变换的分解
除平移变换外,只须对矩阵A 进行分解。
SVD分解
对矩阵A 作奇异值分解(SVD 分解,见第8 章),我们得到A=UDVT,其中U,V 是正交矩阵,D 是对角元为正数的对角矩阵
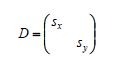
仿射变换是一个等距变换VT、一个非均匀伸缩变换D 以及另一个等距变换U 的合成,因此它与相似变换的差别在于非均匀伸缩。

QR分解
对A 作QR 分解得到A=UK,其中U 是一个正交阵,K 是一个对角元素均大于零的上三角阵:

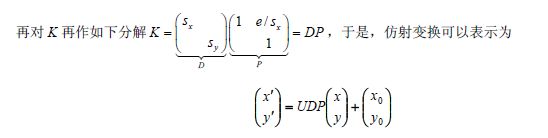

仿射不变量
- 仿射变换保持平行性不变。
- 仿射变换保持面积的比值不变。http://mini.eastday.com/mobile/181004122725427.html#
- 仿射变换保持平行线段长度的比值不变。
- 射影变换H 保持无穷远直线不动的充要条件是H 为仿射变换。(圆环点变了)
二次曲线的仿射分类
射影变换H 保持无穷远直线不动的充要条件是H 为仿射变换。
椭圆与无穷远直线没有实交点
抛物线与无穷远直线相切,即有两个接融点
双曲线与无穷远直线有两个实交点
而仿射变换保持无穷远直线不动且保持交点性质不变(实变实、虚变虚),所以前面的性质是仿射不变的。因此,二次曲线的仿射分类仍然是:椭圆、抛物线与双曲线三类。