浅谈张量分解（五）：稀疏张量的CP分解

在前面的文章中，我们已经讨论了稀疏张量的Tucker分解，并介绍了如何采用梯度下降训练出一个合理的分解结构，与Tucker分解略有不同，这篇文章将介绍在数学表达式上更为简洁的CP分解，同时讨论如何利用梯度下降训练出稀疏张量的CP分解结构。

需要注意的是，本文在撰写过程中尽量避开了繁琐的数学推导，阅读以下内容只需要具备以下几点即可：

• 首先，知道高阶张量实质上是多维数组，且仅仅是向量和矩阵的高阶泛化；
• 其次，对高等数学所学习的求偏导数较为熟悉；
• 最后，对矩阵计算较为熟悉且感兴趣。

1 张量的CP分解模型

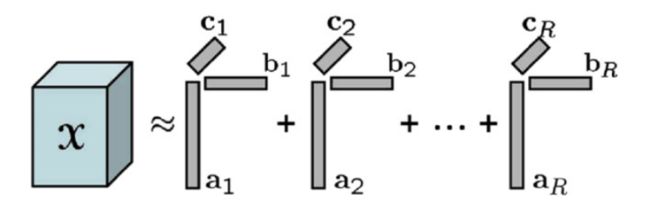
一般而言，给定一个大小为的张量，其CP分解可以写成如下形式，即

其中，矩阵的大小分别为，被称为因子矩阵（factor matrices），符号“”表示张量积，对于向量而言，这里的张量积与外积是等价的。张量任意位置上的元素估计值为

.

 

图1 CP分解示意图（图片来源：Scalable tensor factorizations for incomplete data）

若将该逼近问题转化为一个无约束优化问题，且目标函数为残差的平方和，即

.

知道了要优化的目标函数后，我们就能够通过梯度下降法训练出一个合理的分解结构。另外，对梯度下降法有所了解的读者都知道，梯度下降法的原理很简单，我们只需要掌握高等数学中的求导就可以了。

接下来，我们来看看如何对目标函数求偏导，并给出决策变量的梯度下降更新公式。

2 “元素级”的梯度下降更新公式

将张量被观测到的元素相应的索引集合记为，前面的目标函数可以改写为

对目标函数中的决策变量求偏导数，则我们能够很容易地得到

,

,

.

其中，需要特殊指出的是，求和符号下面的, , 分别表示矩阵被观测到的元素其索引构成的集合。进一步，决策变量的更新公式可以分别写成：

,

,

.

在这些更新公式中，为梯度下降的学习率。到这里，我们会发现，上述过程与前面的浅谈张量分解（一）：如何简单地进行张量分解？一文中对稀疏张量进行Tucker分解的过程完全相同，只不过是目标函数和决策变量略有不同而已。那么问题来了，这篇文章的意义是什么呢？

接下来，我们来看看在运算程序时更为有效的一种梯度下降更新策略，即“矩阵化”的梯度下降更新公式。

3 "矩阵化"的梯度下降更新公式

上面给出的更新公式是以“元素级”的形式，熟悉MATLAB的读者可能也知道，这种形式的更新公式在运算相应的程序时效率是很低的，且不能发挥出MATLAB自身在矩阵计算方面的优势。不过，值得庆幸的是，这些更新公式都具有“矩阵化”的数学表达式。

定义一个与张量大小相同的张量，当时，，否则；再令，则决策变量的更新公式分别为

,

,

.

其中，运算符“”表示点乘（element-wise multiplication），若大小均为的张量和进行点乘，即，则；运算符“”表示Khatri-Rao积，其定义可参考前面的浅谈张量分解（二）：张量分解的数学基础一文。

---------------------一些简单的推导---------------------

以因子矩阵  的更新公式为例，令梯度，由于

 , .

故矩阵  的第  行：

.

由于 ，故该矩阵的第  列为：

 .

综上，我们可以计算出矩阵  的第  行第  列元素为：

 .

从而，我们可以发现，上述“矩阵级”的更新公式表达式与“元素级”等价。

----------------------------------------------------------------

有了这些“矩阵化”的更新公式后，我们还需要考虑一个问题，即对于阶数大于3的稀疏张量如何进行CP分解呢？是否存在类似的梯度下降更新公式呢？

4 延伸：更高阶稀疏张量的CP分解

给定一个大小为的张量，并将其CP分解写成如下形式：

其中，分别是大小为的因子矩阵，采用梯度下降，令，则决策变量的更新公式可以分别写成

,

,

... ...

.

到这里，我们已经介绍完了稀疏张量的CP分解，有兴趣的读者此时就可以设计实验了，不过，需要额外说明的是，CP分解中的一般表示张量的秩（tensor rank），由于对于张量的秩的求解往往是一个NP-hard问题，所以读者在设计实验时要预先给定的值。

5 参考文献

本文主要参考了Scalable tensor factorizations for incomplete data一文，文中介绍了如何利用CP分解来解决张量填补问题（tensor completion problem）。