生成组合(Gray码)
文章目录
- 1 问题描述
- 2 问题转换
- 2.1 生成 { x n − 1 , ⋯ , x 1 , x 0 } \{x_{n-1}, \cdots, x_1, x_0\} {xn−1,⋯,x1,x0}的子集的二进制算法
- 3 Gray码
- 3.1 递归生成反射 G r a y Gray Gray码
- 3.2 迭代生成反射 G r a y Gray Gray码
- 4 参考资料
1 问题描述
设 S S S是 n n n个元素的集合:
S = { x n − 1 , ⋯ , x 1 , x 0 } S=\{x_{n-1}, \cdots, x_1, x_0\} S={xn−1,⋯,x1,x0}
我们想要寻找一种生成 S S S的所有 2 n 2^n 2n个组合(子集)的算法。
2 问题转换
给定 S S S的一个子集 A A A, S S S中的每一个元素 x x x或者属于 A A A或者不属于 A A A。如果用 1 1 1表示属于,用 0 0 0表示不属于,那么就可以把 S S S的 2 n 2^n 2n个子集看成 2 n 2^n 2n个 0 0 0和 1 1 1的 n n n元组:
( a n − 1 , ⋯ , a 1 , a 0 ) = a n − 1 ⋯ a 1 a 0 (a_{n-1}, \cdots, a_1, a_0)= a_{n-1}\cdots a_1a_0 (an−1,⋯,a1,a0)=an−1⋯a1a0
我们可以把 n n n元组看成二进制数,那么这个 n n n元组就和二进制数存在一一对应关系,这下问题就变得简单了。我们可以按从小到大的顺序写出 0 0 0到 2 n − 1 2^{n-1} 2n−1之间的数,但是要用二进制的形式,每次加一都要用二进制算术。
2.1 生成 { x n − 1 , ⋯ , x 1 , x 0 } \{x_{n-1}, \cdots, x_1, x_0\} {xn−1,⋯,x1,x0}的子集的二进制算法
算法步骤:从 a n − 1 ⋯ a 1 a 0 = 0 ⋯ 00 a_{n-1}\cdots a_1a_0=0\cdots 00 an−1⋯a1a0=0⋯00开始。当 a n − 1 ⋯ a 1 a 0 ≠ 1 ⋯ 11 a_{n-1}\cdots a_1a_0 \ne 1\cdots 11 an−1⋯a1a0=1⋯11时执行下面操作:
- 求出使得 a j = 0 a_j = 0 aj=0的最小整数 j j j(在 n − 1 n-1 n−1和 0 0 0之间)
- 用 1 1 1代替 a j a_j aj并用 0 0 0代替 a j − 1 , ⋯ , a 0 a_{j-1}, \cdots,a_0 aj−1,⋯,a0中的每一个(根据我们对 j j j的选择可知,在用 0 0 0代替以前它们都等于 1 1 1)。
这种通过二进制的生成方案所产生的的 0 , 1 0,1 0,1的 n n n元组的顺序称为 n n n元组的字典序。在把 0 , 1 0,1 0,1的 n n n元组的字典序看成是集合 { x n − 1 , ⋯ , x 1 , x 0 } \{x_{n-1}, \cdots, x_1, x_0\} {xn−1,⋯,x1,x0}的子集的顺序时,有时它也被叫做子集的压缩序。
3 Gray码
在子集压缩序中,一个自己的直接后继可能与这个子集本身差异非常大。子集 A = { x 6 , x 4 , x 3 } A=\{x_6,x_4,x_3\} A={x6,x4,x3}(对应于 1011000 1011000 1011000)紧随子集 B = { x 6 , x 4 , x 2 , x 1 , x 0 } B=\{x_6, x_4, x_2, x_1, x_0\} B={x6,x4,x2,x1,x0}(对应于 1010111 1010111 1010111)之后,但是二者的元素差异非常大。这就引出了一个问题:是否有可能以不同的顺序生成 n n n元素集合的自己,使得一个子集的直接后继与其本身的差异尽可能小?这里的尽可能小指的是一个子集的直接后继是在通过增加一个新元素或者删除一个老元素,但二者不同时进行的前提下得到的。例如:
000 001 011 010 110 111 101 100 000\\ 001\\ 011\\ 010\\ 110\\ 111\\ 101\\ 100 000001011010110111101100
我们可以用超方体的顶点来表示每一个 n n n元组,因为 Q k Q_k Qk的顶点数量就是 2 k 2^k 2k。例如下面的 Q 2 Q_2 Q2:
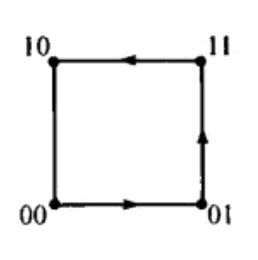
生成只在一个位置上与 n n n元组不同的其后继 n n n元组的算法对应于沿着 Q k Q_k Qk的边遍历该超方体的每个顶点一次。任意一个这样的遍历(或 n n n元组的最终列表)称为 n n n阶 G r a y Gray Gray码。如果遍历可以再经过一条边从终点回到起点,那么就称这个 G r a y Gray Gray码是循环的。例如上图对应的 2 2 2阶 G r a y Gray Gray码为:
00 01 11 10 00\\ 01\\ 11\\ 10 00011110
Q 3 Q_3 Q3可以通过拷贝上图并把每一个顶点的前面加上 1 1 1,然后上图本身的顶点前面加上 0 0 0,然后连接对应顶点得到:
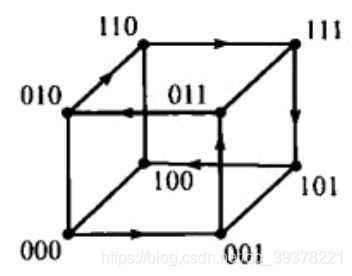
通过箭头方向的遍历我们得到 3 3 3阶级 G r a y Gray Gray码:
000 001 011 010 110 111 101 100 000\\ 001\\ 011\\ 010\\ 110\\ 111\\ 101\\ 100 000001011010110111101100
我们可以持续地以这种方式对任意的整数 n ≥ 1 n\ge 1 n≥1递归地构建 n n n阶 G r a y Gray Gray码。用这种方式构建的 G r a y Gray Gray称为反射 G r a y Gray Gray码
3.1 递归生成反射 G r a y Gray Gray码
递归定义:
- 1 1 1阶反射 G r a y Gray Gray码是 0 1 \begin{matrix}0\\1\end{matrix} 01
- 假设 n > 1 n\gt 1 n>1且已经构建好了 n − 1 n-1 n−1阶反射 G r a y Gray Gray码。为了构建 n n n阶反射 G r a y Gray Gray码,首先,以 n − 1 n-1 n−1阶反射 G r a y Gray Gray码所给出的顺序列出 0 , 1 0,1 0,1的 ( n − 1 ) (n-1) (n−1)元组,并把一个 0 0 0添加到每个 ( n − 1 ) (n-1) (n−1)元组左边,然后再以 ( n − 1 ) (n-1) (n−1)阶反射 G r a y Gray Gray码所给顺序的相反顺序列出 0 , 1 0,1 0,1的 ( n − 1 ) (n-1) (n−1)元组,并把一个 1 1 1添加到每个 ( n − 1 ) (n-1) (n−1)元组左边。
下面使用字符串的形式实现了一下这个递归生成反射 G r a y Gray Gray码算法:
def Gray_recursive(n):
if n == 1:
return ["0", "1"]
arr0 = Gray_recursive(n - 1)
arr1 = copy.deepcopy(arr0)
for i in range(2**(n-1)):
arr0[i] = "0" + arr0[i]
arr1[i] = "1" + arr1[i]
return arr0 + arr1[::-1]
输入:4
输出:
0000
0001
0011
0010
0110
0111
0101
0100
1100
1101
1111
1110
1010
1011
1001
1000
3.2 迭代生成反射 G r a y Gray Gray码
递归的方法依赖于 n − 1 n-1 n−1阶的反射 G r a y Gray Gray码,下面给出反射 G r a y Gray Gray码在从一个 n n n元组走到下一个 n n n元组时,需要在哪个地方改变。首先定义:
σ ( a n − 1 ⋯ a 1 a 0 ) = a n − 1 + ⋯ + a 1 + a 0 \sigma(a_{n-1}\cdots a_1a_0)=a_{n-1}+\cdots +a_1+a_0 σ(an−1⋯a1a0)=an−1+⋯+a1+a0
即 1 1 1的个数。
算法步骤:从 n n n元组 a n − 1 ⋯ a 1 a 0 = 0 ⋯ 00 a_{n-1}\cdots a_1a_0=0\cdots 00 an−1⋯a1a0=0⋯00开始,当 a n − 1 ⋯ a 1 a 0 ≠ 10 ⋯ 0 a_{n-1}\cdots a_1a_0 \ne10\cdots 0 an−1⋯a1a0=10⋯0时执行下面操作:
- 计算 σ ( a n − 1 ⋯ a 1 a 0 ) \sigma(a_{n-1}\cdots a_1a_0) σ(an−1⋯a1a0)
- 如果 σ ( a n − 1 ⋯ a 1 a 0 ) \sigma(a_{n-1}\cdots a_1a_0) σ(an−1⋯a1a0)是偶数,则改变 a 0 a_0 a0
- 如果 σ ( a n − 1 ⋯ a 1 a 0 ) \sigma(a_{n-1}\cdots a_1a_0) σ(an−1⋯a1a0)是奇数,确定这样的 j j j使得 a j = 1 a_j=1 aj=1且对满足 j > i j\gt i j>i的所有 i i i有 a i = 0 a_i=0 ai=0(即这是从右边开始的第一个 1 1 1),然后,改变 a j + 1 a_{j+1} aj+1。
下面还是以字符串的形式实现了一下这个过程:
def Gray_iterate(n):
res = ["0"*n]
for i in range(1, 2**n):
if res[-1].count("1") % 2 == 0:
if res[-1][-1] == "0":
res.append(res[-1][:-1] + "1")
else:
res.append(res[-1][:-1] + "0")
else:
j = res[-1].rindex("1")
if res[-1][j-1] == "0":
res.append(res[-1][:j-1] + "1" + res[-1][j:])
else:
res.append(res[-1][:j-1] + "0" + res[-1][j:])
return res
输入:4
输出:
0000
0001
0011
0010
0110
0111
0101
0100
1100
1101
1111
1110
1010
1011
1001
1000
4 参考资料
- 《组合数学》第五版 P60-P67