111. Minimum Depth of Binary Tree
这道题看上去很简单,求的是到叶子节点最短路径的节点的个数,其实并不是,当一个节点只有一个子节点的时候,如果按照求路径长度的求解方式的话,得到的长度会是1,因为有一边是0。但此时并不是到达了叶子节点。因此对于只有一个叶子节点的情况,我们要让这一边的长度变为一个很大的数,确保我们返回的是另一个叶子节点的路径长度。
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public int minDepth(TreeNode root) {
if(root==null)
return 0;
if(root.left == null && root.right == null)
return 1;
int left = root.left!=null ? minDepth(root.left):0xfffffff;
int right = root.right!= null ?minDepth(root.right):0xfffffff;
return Math.min(left,right) + 1;
}
}
112. Path Sum
回溯法
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public boolean hasPathSum(TreeNode root, int sum) {
if(root==null)
return false;
return subPathSum(root,sum,root.val);
}
public boolean subPathSum(TreeNode root,int sum,int subsum){
if(subsum == sum && root.left == null && root.right == null){
return true;
}
if(root.left != null)
if(subPathSum(root.left,sum,subsum + root.left.val))
return true;
if(root.right !=null)
if(subPathSum(root.right,sum,subsum + root.right.val))
return true;
return false;
}
}
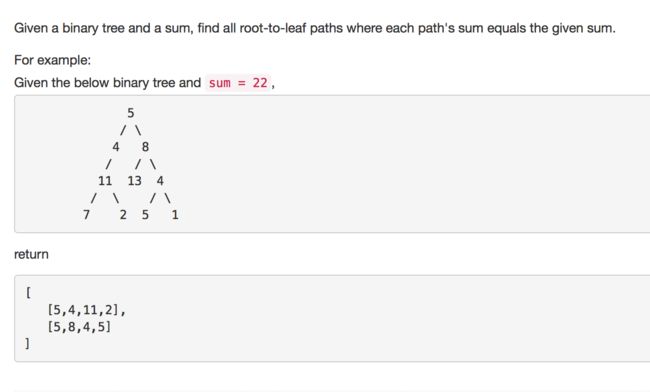
113. Path Sum II
回溯法
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public List> pathSum(TreeNode root, int sum) {
List> res = new ArrayList>();
if(root==null)
return res;
addPath(res,root,sum,new ArrayList());
return res;
}
public void addPath(List> res,TreeNode root,int sum,List arr){
if(root.val==sum && root.left==null && root.right==null){
arr.add(root.val);
res.add(new ArrayList(arr));
arr.remove(arr.size()-1);
return;
}
if(root.left!=null){
arr.add(root.val);
addPath(res,root.left,sum-root.val,arr);
arr.remove(arr.size()-1);
}
if(root.right!=null){
arr.add(root.val);
addPath(res,root.right,sum-root.val,arr);
arr.remove(arr.size()-1);
}
}
}
114. Flatten Binary Tree to Linked List
递归的思路,先处理右子树,如果有左子树的话,首先找到左子树的最后一个节点,然后将左子树拼接到根节点和右子树之间。
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public void flatten(TreeNode root) {
if(root==null)
return;
flatten(root.right);
if(root.left!=null){
flatten(root.left);
TreeNode lefttail = root.left;
while(lefttail.right!=null)
lefttail = lefttail.right;
lefttail.right = root.right;
root.right = root.left;
root.left = null;
}
}
}
115. Distinct Subsequences
回溯法,超时
class Solution {
int count = 0;
public int numDistinct(String s, String t) {
if(s==null || s.length()==0)
return count;
backtracking(s,t,0,0);
return count;
}
public void backtracking(String s,String t,int start1,int start2){
if(start2==t.length()){
count++;
return;
}
for(int i=start1;i<(s.length()-t.length()+start2+1);i++){
if(s.charAt(i)==t.charAt(start2))
backtracking(s,t,i+1,start2+1);
}
}
}
动态规划法
维护一个二维表格。
class Solution {
public int numDistinct(String s, String t) {
int[][] res = new int[s.length()+1][t.length()+1];
res[0][0] = 1;
for(int i=1;i116. Populating Next Right Pointers in Each Node
层次遍历的思路:
/**
* Definition for binary tree with next pointer.
* public class TreeLinkNode {
* int val;
* TreeLinkNode left, right, next;
* TreeLinkNode(int x) { val = x; }
* }
*/
public class Solution {
public void connect(TreeLinkNode root) {
if(root==null)
return;
Queue queue = new LinkedList();
Queue row = new LinkedList();
queue.offer(root);
while(!queue.isEmpty()){
while(!queue.isEmpty()){
row.offer(queue.poll());
}
while(!row.isEmpty()){
TreeLinkNode t = row.poll();
if(t.left!=null)
queue.offer(t.left);
if(t.right!=null)
queue.offer(t.right);
t.next = row.peek()==null?null:row.peek();
}
}
}
}
117. Populating Next Right Pointers in Each Node II
层次遍历的思路同样适用:
/**
* Definition for binary tree with next pointer.
* public class TreeLinkNode {
* int val;
* TreeLinkNode left, right, next;
* TreeLinkNode(int x) { val = x; }
* }
*/
public class Solution {
public void connect(TreeLinkNode root) {
if(root==null)
return;
Queue queue = new LinkedList();
Queue row = new LinkedList();
queue.offer(root);
while(!queue.isEmpty()){
while(!queue.isEmpty()){
row.offer(queue.poll());
}
while(!row.isEmpty()){
TreeLinkNode t = row.poll();
if(t.left!=null)
queue.offer(t.left);
if(t.right!=null)
queue.offer(t.right);
t.next = row.peek()==null?null:row.peek();
}
}
}
}
118. Pascal's Triangle
class Solution {
public List> generate(int numRows) {
List> res = new ArrayList>();
for(int i=1;i<=numRows;i++){
List row = new ArrayList();
if(i==1)
row.add(1);
else if(i==2){
row.add(1);
row.add(1);
}
else{
row.add(1);
for(int j=1;j 119. Pascal's Triangle II
这里要注意的是,我们只能用常数空间,所以用一个大小为k的数组保存结果,每走一行更新一次,但是要注意,我们不能从前面更新,举例来说,第二行为[1,2,1],在更新第三行时,使用公式 list[j] = list[j-1] + list[j],那么会变成[1,3,4,1],而正确的结果应该是[1,3,3,1],这是因为在得到第二个3时,本来的list[j-1]已经由2变为3了,所以我们要从后往前更新。
class Solution {
public List getRow(int rowIndex) {
int[] list = new int[rowIndex+1];
for(int i=0;i=1;j--)
list[j] = list[j-1] + list[j];
list[i] = 1;
}
}
List res = new ArrayList();
int index = 0;
while(index<=rowIndex && list[index]!=0)
res.add(list[index++]);
return res;
}
}
120. Triangle
使用动态规划的方法。
class Solution {
public int minimumTotal(List> triangle) {
if(triangle==null || triangle.size()==0)
return 0;
int[][] res = new int[triangle.size()][triangle.size()];
int min = 0xfffffff;
for(int i=0;i