Andres_Lionel
Andres_Lionel

牛牛的等差数列【线段树】

牛牛的等差数列【线段树】_第1张图片

题目链接

  这里的突破口在于小于等于25且大于等于3的质数连乘在1e8左右，所以，我们可以在操作上，将其看作对1e8去求模，而不是对每个都进行预处理。

时间复杂度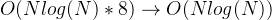O(N log(N) * 8)\rightarrow O(N log(N))。也就是说，我们排除这个预处理之后，直接就是降了10倍左右的复杂度。

  然后，给区间一个等差数列，可以看成给这段区间赋一个基础值和递增一个值，所以我们在线段树上操作的时候，维护两个懒标记，分别是基础值，和等差值。因为存在累加（线性）关系，所以直接利用累加即可。

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
//#include 
//#include 
#define lowbit(x) ( x&(-x) )
#define pi 3.141592653589793
#define e 2.718281828459045
#define INF 0x3f3f3f3f
#define Big_INF 0x3f3f3f3f3f3f3f3f
#define eps 1e-8
#define HalF (l + r)>>1
#define lsn rt<<1
#define rsn rt<<1|1
#define Lson lsn, l, mid
#define Rson rsn, mid+1, r
#define QL Lson, ql, qr
#define QR Rson, ql, qr
#define myself rt, l, r
#define MP(a, b) make_pair(a, b)
using namespace std;
typedef unsigned long long ull;
typedef unsigned int uit;
typedef long long ll;
const int maxN = 2e5 + 7;
const ull mod[8] = {3, 5, 7, 11, 13, 17, 19, 23};
const ull MOD = 3 * 5 * 7 * 11 * 13 * 17 * 19 * 23;
inline int _ID(ull mx) { return (int)(lower_bound(mod, mod + 8, mx) - mod); }
int N, Q;
ull a[maxN], tree[maxN << 2], sum[maxN << 2], del[maxN << 2];
bool lazy[maxN << 2] = {false};
inline void pushup(int rt) { tree[rt] = (tree[lsn] + tree[rsn]) % MOD; }
void buildTree(int rt, int l, int r)
{
    if(l == r) { tree[rt] = a[l] % MOD; return; }
    int mid = HalF;
    buildTree(Lson); buildTree(Rson);
    pushup(rt);
}
inline void pushdown(int rt, int l, int r)
{
    if(lazy[rt])
    {
        int mid = HalF; ull len_L = mid - l + 1, len_R = r - mid;
        lazy[lsn] = lazy[rsn] = true;
        sum[lsn] = (sum[lsn] + sum[rt]) % MOD;
        del[lsn] = (del[lsn] + del[rt]) % MOD;
        tree[lsn] = (tree[lsn] + sum[rt] * len_L + (len_L - 1LL) * len_L / 2LL % MOD * del[rt] % MOD) % MOD;
        sum[rsn] = (sum[rsn] + sum[rt] + del[rt] * len_L) % MOD;
        del[rsn] = (del[rsn] + del[rt]) % MOD;
        tree[rsn] = (tree[rsn] + (sum[rt] + del[rt] * len_L) % MOD * len_R + (len_R - 1LL) * len_R / 2LL % MOD * del[rt]) % MOD;
        sum[rt] = del[rt] = 0;
        lazy[rt] = false;
    }
}
void update(int rt, int l, int r, int ql, int qr, ull val, ull d)
{
    if(ql <= l && qr >= r)
    {
        ull fir_v = (val + d * (l - ql)) % MOD;
        lazy[rt] = true;
        sum[rt] = (sum[rt] + fir_v) % MOD;
        del[rt] = (del[rt] + d) % MOD;
        tree[rt] = (tree[rt] + fir_v * (r - l + 1) % MOD + (ull)(r - l) * (r - l + 1) / 2LL * d) % MOD;
        return;
    }
    pushdown(myself);
    int mid = HalF;
    if(qr <= mid) update(QL, val, d);
    else if(ql > mid) update(QR, val, d);
    else { update(QL, val, d); update(QR, val, d); }
    pushup(rt);
}
ull query(int rt, int l, int r, int ql, int qr, int op)
{
    if(ql <= l && qr >= r) return tree[rt] % mod[op];
    pushdown(myself);
    int mid = HalF;
    if(qr <= mid) return query(QL, op);
    else if(ql > mid) return query(QR, op);
    else return (query(QL, op) + query(QR, op)) % mod[op];
}
int main()
{
    scanf("%d", &N);
    for(int i=1; i<=N; i++) scanf("%lld", &a[i]);
    buildTree(1, 1, N);
    scanf("%d", &Q); int op, l, r, v, d;
    while(Q--)
    {
        scanf("%d", &op);
        if(op == 1)
        {
            scanf("%d%d%d%d", &l, &r, &v, &d);
            update(1, 1, N, l, r, v, d);
        }
        else
        {
            scanf("%d%d%d", &l, &r, &d);
            printf("%lld\n", query(1, 1, N, l, r, _ID(d)));
        }
    }
    return 0;
}

 

你可能感兴趣的:(数据结构,线段树)

  • 数组去重 好奇的猫猫猫
    整理自js中基础数据结构数组去重问题思考？如何去除数组中重复的项例如数组：[1,3,4,3,5]我们在做去重的时候，一开始想到的肯定是，逐个比较，外面一层循环，内层后一个与前一个一比较，如果是久不将当前这一项放进新的数组，挨个比较完之后返回一个新的去过重复的数组不好的实践方式上述方法效率极低，代码量还多，思考？有没有更好的方法这时候不禁一想当然有了！！！hashtable啊，通过对象的hash办法
  • 回溯算法-重新安排行程 chirou_ 算法数据结构图论c++图搜索
    leetcode332.重新安排行程这题我还没自己ac过，只能现在凭着刚学完的热乎劲把我对题解的理解记下来。本题我认为对数据结构的考察比较多，用什么数据结构去存数据，去读取数据，都是很重要的。classSolution{private:unordered_map>targets;boolbacktracking(intticketNum,vector&result){//1.确定参数和返回值//2
  • Redis系列：Geo 类型赋能亿级地图位置计算 Ly768768 redisbootstrap数据库
    1前言我们在篇深刻理解高性能Redis的本质的时候就介绍过Redis的几种基本数据结构，它是基于不同业务场景而设计的：动态字符串(REDIS_STRING)：整数(REDIS_ENCODING_INT)、字符串(REDIS_ENCODING_RAW)双端列表(REDIS_ENCODING_LINKEDLIST)压缩列表(REDIS_ENCODING_ZIPLIST)跳跃表(REDIS_ENCODI
  • Faiss：高效相似性搜索与聚类的利器 网络·魚 大数据faiss
    Faiss是一个针对大规模向量集合的相似性搜索库，由FacebookAIResearch开发。它提供了一系列高效的算法和数据结构，用于加速向量之间的相似性搜索，特别是在大规模数据集上。本文将介绍Faiss的原理、核心功能以及如何在实际项目中使用它。Faiss原理：近似最近邻搜索：Faiss的核心功能之一是近似最近邻搜索，它能够高效地在大规模数据集中找到与给定查询向量最相似的向量。这种搜索是近似的，
  • 数据结构之哈希表 X同学的开始 数据结构数据结构散列表
    哈希表(散列表)出现的原因在顺序表中查找时，需要从表头开始，依次遍历比较a[i]与key的值是否相等，直到相等才返回索引i；在有序表中查找时，我们经常使用的是二分查找，通过比较key与a[i]的大小来折半查找，直到相等时才返回索引i。最终通过索引找到我们要找的元素。但是，这两种方法的效率都依赖于查找中比较的次数。我们有一种想法，能不能不经过比较，而是直接通过关键字key一次得到所要的结果呢？这时，
  • Python开发常用的三方模块如下： 换个网名有点难 python开发语言
    Python是一门功能强大的编程语言，拥有丰富的第三方库，这些库为开发者提供了极大的便利。以下是100个常用的Python库，涵盖了多个领域：1、NumPy，用于科学计算的基础库。2、Pandas，提供数据结构和数据分析工具。3、Matplotlib，一个绘图库。4、Scikit-learn，机器学习库。5、SciPy，用于数学、科学和工程的库。6、TensorFlow，由Google开发的开源机
  • 数据结构 | 栈和队列 TT-Kun 数据结构与算法数据结构栈队列C语言
    文章目录栈和队列1.栈：后进先出（LIFO）的数据结构1.1概念与结构1.2栈的实现2.队列：先进先出（FIFO）的数据结构2.1概念与结构2.2队列的实现3.栈和队列算法题3.1有效的括号3.2用队列实现栈3.3用栈实现队列3.4设计循环队列结论栈和队列在计算机科学中，栈和队列是两种基本且重要的数据结构，它们在处理数据存储和访问顺序方面有着独特的规则和应用。本文将详细介绍栈和队列的概念、结构、实
  • [Python] 数据结构 详解及代码 AIAdvocate 算法python数据结构链表
    今日内容大纲介绍数据结构介绍列表链表1.数据结构和算法简介程序大白话翻译,程序=数据结构+算法数据结构指的是存储,组织数据的方式.算法指的是为了解决实际业务问题而思考思路和方法,就叫:算法.2.算法的5大特性介绍算法具有独立性算法是解决问题的思路和方式,最重要的是思维,而不是语言,其(算法)可以通过多种语言进行演绎.5大特性有输入,需要传入1或者多个参数有输出,需要返回1个或者多个结果有穷性,执行
  • 4.C_数据结构_队列 荣世蓥 数据结构数据结构
    概述什么是队列：队列是限定在两端进行插入操作和删除操作的线性表。具有先入先出(FIFO)的特点相关名词：队尾：写入数据的一段队头：读取数据的一段空队：队列中没有数据，队头指针=队尾指针满队：队列中存满了数据，队尾指针+1=队头指针循环队列1、基本内容循环队列是以数组形式构成的队列数据结构。循环队列的结构体如下：typedefintdata_t;//队列数据类型#defineN64//队列容量typ
  • C++八股 Petrichorzncu 八股总结c++开发语言
    这里写目录标题C++内存管理C++的构造函数，复制构造函数，和析构函数深复制与浅复制：构造函数和析构函数哪个能写成虚函数，为什么？C++数据结构内存排列结构体和类占用的内存：==虚函数和虚表的原理==虚函数虚表（Vtable）虚函数和虚表的实现细节==内存泄漏==指针的工作原理函数的传值和传址new和delete与malloc和freeC++内存区域划分C++11新特性C++常见新特性==智能指针
  • 【树一线性代数】005入门 Owlet_woodBird 算法
    Index本文稍后补全，推荐阅读：https://blog.csdn.net/weixin_60702024/article/details/141874376分析实现总结本文稍后补全，推荐阅读：https://blog.csdn.net/weixin_60702024/article/details/141874376已知非空二叉树T的结点值均为正整数，采用顺序存储方式保存，数据结构定义如下:t
  • python获取子进程返回值_Python对进程Multiprocessing子进程返回值 weixin_39752157 python获取子进程返回值
    在实际使用多进程的时候，可能需要获取到子进程运行的返回值。如果只是用来存储，则可以将返回值保存到一个数据结构中；如果需要判断此返回值，从而决定是否继续执行所有子进程，则会相对比较复杂。另外在Multiprocessing中，可以利用Process与Pool创建子进程，这两种用法在获取子进程返回值上的写法上也不相同。这篇中，我们直接上代码，分析多进程中获取子进程返回值的不同用法，以及优缺点。初级用法
  • 【数据结构-一维差分】力扣2848. 与车相交的点 hlc@ 数据结构数据结构leetcode算法
    给你一个下标从0开始的二维整数数组nums表示汽车停放在数轴上的坐标。对于任意下标i，nums[i]=[starti,endi]，其中starti是第i辆车的起点，endi是第i辆车的终点。返回数轴上被车任意部分覆盖的整数点的数目。示例1：输入：nums=[[3,6],[1,5],[4,7]]输出：7解释：从1到7的所有点都至少与一辆车相交，因此答案为7。示例2：输入：nums=[[1,3],[5
  • JavaScript `Map` 和 `WeakMap`详细解释 跳房子的前端 JavaScript原生方法javascript前端开发语言
    在JavaScript中，Map和WeakMap都是用于存储键值对的数据结构，但它们有一些关键的不同之处。MapMap是一种可以存储任意类型的键值对的集合。它保持了键值对的插入顺序，并且可以通过键快速查找对应的值。Map提供了一些非常有用的方法和属性来操作这些数据对：set(key,value):将一个键值对添加到Map中。如果键已经存在，则更新其对应的值。get(key):获取指定键的值。如果键
  • 【高阶数据结构】并查集 椿融雪 数据结构与算法数据结构并查集
    文章目录一、并查集原理二、并查集实现三、并查集应用一、并查集原理在一些应用问题中，需要将n个不同的元素划分成一些不相交的集合。开始时，每个元素自成一个单元素集合，然后按一定的规律将归于同一组元素的集合合并。在此过程中要反复用到查询某一个元素归属于那个集合的运算。适合于描述这类问题的抽象数据类型称为并查集(union-findset)。比如：某公司今年校招全国总共招生10人，西安招4人，成都招3人，
  • python中文版软件下载-Python中文版 编程大乐趣
    python中文版是一种面向对象的解释型计算机程序设计语言。python中文版官网面向对象编程，拥有高效的高级数据结构和简单而有效的方法，其优雅的语法、动态类型、以及天然的解释能力，让它成为理想的语言。软件功能强大，简单易学，可以帮助用户快速编写代码，而且代码运行速度非常快，几乎可以支持所有的操作系统，实用性真的超高的。python中文版软件介绍：python中文版的解释器及其扩展标准库的源码和编
  • 开发游戏的学习规划 杰克逊的日记 游戏学习
    第一阶段：●C#语言快速系统地学习一遍（基础的语法、面向对象、基础的数据结构、基础的设计模式）●Unity的2D和3D部分及UI、动画、物理系统●阶段性测验：需要去用前面所学的这些基础知识来完成一个简单的2d或者3d的案例，将通过一个自制的《Flappybird》游戏案例讲解游戏开发的思想及方法，并将《Flappybird》这个游戏进一步改造成一个横版射击类游戏《Crazybird》以巩固并且升华
  • 六、全局锁和表锁：给表加个字段怎么有这么多阻碍 nieniemin
    数据库锁设计的初衷是处理并发问题。作为多用户共享的资源，当出现并发访问的时候，数据库需要合理地控制资源的访问规则。而锁就是用来实现这些访问规则的重要数据结构。根据加锁的范围，MySQL里面的锁大致可以分成全局锁、表级锁和行锁三类。6.1全局锁全局锁就是对整个数据库实例加锁。MySQL提供了一个加全局读锁的方法，命令是Flushtableswithreadlock(FTWRL)。当你需要让整个库处于
  • Golang Channel PandaSkr golang
    Channel解析1.Channel源码分析1.1Channel数据结构typehchanstruct{qcountuint//channel的元素数量dataqsizuint//channel循环队列长度bufunsafe.Pointer//指向循环队列的指针elemsizeuint16//元素大小closeduint32//channel是否关闭0-未关闭elemtype*_type//元素类
  • ⭐算法入门⭐《归并排序》简单01 —— LeetCode 21. 合并两个有序链表 英雄哪里出来 《LeetCode算法全集》算法数据结构链表c++归并排序
    饭不食，水不饮，题必须刷C语言免费动漫教程，和我一起打卡！《光天化日学C语言》LeetCode太难？先看简单题！《C语言入门100例》数据结构难？不存在的！《数据结构入门》LeetCode太简单？算法学起来！《夜深人静写算法》文章目录一、题目1、题目描述2、基础框架3、原题链接二、解题报告1、思路分析2、时间复杂度3、代码详解三、本题小知识一、题目1、题目描述  将两个不降序链表合并为一个新的不降
  • 数据结构 1 五花肉村长 数据结构算法开发语言c语言visualstudio
    1.什么是数据结构数据结构（DataStructure）是计算机存储和组织数据的方式，是指相互之间存在的一种或多种特定关系的数据元的集合。2.什么是算法算法（Algorithm）就是定义良好的计算过程，他取一个或一组的值为输入，并产生出一个或一组值作为输出。简单来说算法就是一系列的计算步骤，用来将输入数据转化成输出结果。3.数据结构和算法的书籍资料学习完数据结构知识，可以去看《剑指offer》和《
  • 【数据结构和算法实践-树-LeetCode113-路径总和Ⅱ】 NeVeRMoRE_2024 数据结构与算法实践数据结构算法leetcodeb树
    数据结构和算法实践-树-LeetCode113-路径总和Ⅱ题目MyThought代码示例JAVA-8题目给你二叉树的根节点root和一个整数目标和targetSum，找出所有从根节点到叶子节点路径总和等于给定目标和的路径。叶子节点是指没有子节点的节点输入：root=[5,4,8,11,null,13,4,7,2,null,null,5,1],targetSum=22输出：[[5,4,11,2],[
  • 【Python】数据结构,链表,算法详解 AIAdvocate python数据结构链表排序算法广度优先深度优先
    今日内容大纲介绍自定义代码-模拟链表删除节点查找节点算法入门-排序类的冒泡排序选择排序插入排序快速排序算法入门-查找类的二分查找-递归版二分查找-非递归版分线性结构-树介绍基本概述特点和分类自定义代码-模拟二叉树1.自定义代码-模拟链表完整版"""案例:自定义代码,模拟链表.​背景: 顺序表在存储数据的时候,需要使用到连续的空间,如果空间不够,就会导致扩容失败,针对于这种情况,我们可以通过链表实现
  • AI教你学Python 第4天：函数和模块 凡人的AI工具箱 AI教你学Pythonpython开发语言人工智能AIGC
    第四天：数据结构一、什么是数据结构？数据结构是计算机科学中用于组织和存储数据的特定方式。良好的数据结构能够提高数据的访问效率、修改频率和管理能力。Python提供了多种内置数据结构，如列表、元组、字典和集合，便于开发者更有效地处理数据。二、Python中的基本数据结构1.列表（List）定义：列表是一个有序的可变集合，允许重复元素。使用方括号[]表示。#示例：定义一个列表fruits=['appl
  • 互联网 Java 工程师面试题（Java 面试题四） 苹果酱0567 面试题汇总与解析java中间件开发语言springboot后端
    下面列出这份Java面试问题列表包含的主题多线程，并发及线程基础数据类型转换的基本原则垃圾回收（GC）Java集合框架数组字符串GOF设计模式SOLID抽象类与接口Java基础，如equals和hashcode泛型与枚举JavaIO与NIO常用网络协议Java中的数据结构和算法正则表达式JVM底层Java最佳实JDBCDate,Time与CalendarJava处理XMLJUnit编程现在是时候给
  • C# Tuple、ValueTuple 語衣 C#知识补充c#
    栏目总目录TupleTuple是C#4.0引入的一个新特性，主要用于存储一个固定数量的元素序列，且这些元素可以具有不同的类型。Tuple是一种轻量级的数据结构，非常适合用于临时存储数据，而无需定义完整的类或结构体。优点简便性：可以快速创建一个包含多个不同类型数据的对象，而无需定义新的类或结构体。灵活性：元素数量和类型在编译时确定，但可以在不同上下文中重复使用不同元素的Tuple。缺点性能：作为引用
  • Rust中的所有权和借用规则详解 代码云1 rust开发语言后端
    Rust是一种系统编程语言，其设计目标包括内存安全、并发安全以及性能。为了实现这些目标，Rust引入了一系列独特的编程概念，其中最为核心的就是所有权（Ownership）和借用（Borrowing）规则。本文将详细解释Rust中的所有权和借用规则，以及它们如何确保内存安全和并发安全。一、所有权规则在Rust中，每一个值都有一个与之关联的所有者。这个所有者可以是变量、数据结构或者是其他形式的存储。所
  • BZOJ 五月胡乱补题 nike0good 其他屯题bzoj博客补档
    旧博客搬运部分格式还没来得及改T_T【BZOJ4806:炮】同BZOJ1801【BZOJ3242:[Noi2013]快餐店】树形dp，要么最远点在同一颗树上（dp），要么在不同树上，此时答案=去掉任何一条边后形成的树的答案的最小值，我们枚举去掉的那条边。由于答案=s[i]-s[j]+dis[i]+dis[j]，i，j可以分开考虑，也可以用线段树解决。【BZOJ4878:[Lydsy2017年5月月
  • 二叉树--python 电子海鸥 Python数据结构与算法python开发语言数据结构
    二叉树一、概述1、介绍是一种非线性数据结构，将数据一分为二，代表根与叶的派生关系，和链表的结构类似，二叉树的基本单元是结点，每个节点包括值和左右子节点引用。每个节点都有两个引用（类似于双向链表），分别指向左子节点和右子节点，该节点被称为这两个子节点的父节点。当给定一个二叉树的结点时，我们将在该节点的左子节点以及其以下结点所形成的树称为左子树，同理，右子节点的部分被称为右子树。在二叉树中，除了叶节点
  • 使用WAF防御网络上的隐蔽威胁之反序列化攻击 baiolkdnhjaio 网络安全
    什么是反序列化反序列化是将数据结构或对象状态从某种格式转换回对象的过程。这种格式通常是二进制流或者字符串（如JSON、XML），它是对象序列化（即对象转换为可存储或可传输格式）的逆过程。反序列化的安全风险反序列化的安全风险主要来自于处理不受信任的数据源时的不当反序列化。如果应用程序反序列化了恶意构造的数据，攻击者可能能够执行代码、访问敏感数据、进行拒绝服务攻击等。这是因为反序列化过程中可能会自动触
  • 用MiddleGenIDE工具生成hibernate的POJO（根据数据表生成POJO类） AdyZhang POJOeclipseHibernateMiddleGenIDE
    推荐:MiddlegenIDE插件,   是一个Eclipse   插件.     用它可以直接连接到数据库,   根据表按照一定的HIBERNATE规则作出BEAN和对应的XML ，用完后你可以手动删除它加载的JAR包和XML文件!     今天开始试着使用
  • .9.png Cb123456 android
      “点九”是andriod平台的应用软件开发里的一种特殊的图片形式，文件扩展名为：.9.png 　　智能手机中有自动横屏的功能,同一幅界面会在随着手机(或平板电脑)中的方向传感器的参数不同而改变显示的方向,在界面改变方向后,界面上的图形会因为长宽的变化而产生拉伸,造成图形的失真变形。 　　我们都知道android平台有多种不同的分辨率，很多控件的切图文件在被放大拉伸后，边
  • 算法的效率 天子之骄 算法效率复杂度最坏情况运行时间大O阶平均情况运行时间
    算法的效率 效率是速度和空间消耗的度量。集中考虑程序的速度，也称运行时间或执行时间，用复杂度的阶(O)这一标准来衡量。空间的消耗或需求也可以用大O表示，而且它总是小于或等于时间需求。   以下是我的学习笔记：   1.求值与霍纳法则，即为秦九韶公式。   2.测定运行时间的最可靠方法是计数对运行时间有贡献的基本操作的执行次数。运行时间与这个计数成正比。
  • java数据结构 何必如此 java数据结构
    Java 数据结构 Java工具包提供了强大的数据结构。在Java中的数据结构主要包括以下几种接口和类： 枚举（Enumeration） 位集合（BitSet） 向量（Vector） 栈（Stack） 字典（Dictionary） 哈希表（Hashtable） 属性（Properties） 以上这些类是传统遗留的，在Java2中引入了一种新的框架-集合框架(Collect
  • MybatisHelloWorld 3213213333332132
    //测试入口TestMyBatis package com.base.helloworld.test; import java.io.IOException; import org.apache.ibatis.io.Resources; import org.apache.ibatis.session.SqlSession; import org.apache.ibat
  • Java|urlrewrite|URL重写|多个参数 7454103 javaxmlWeb工作
     个人工作经验！ 如有不当之处，敬请指点 1.0  web -info 目录下建立     urlrewrite.xml  文件 类似如下： <?xml version="1.0" encoding="UTF-8" ?>   <!DOCTYPE u
  • 达梦数据库+ibatis darkranger sqlmysqlibatisSQL Server
    --插入数据方面 如果您需要数据库自增... 那么在插入的时候不需要指定自增列. 如果想自己指定ID列的值, 那么要设置 set identity_insert  数据库名.模式名.表名; ----然后插入数据; example: create table zhabei.test( id bigint identity(1,1) primary key, nam
  • XML 解析 四种方式 aijuans android
    XML现在已经成为一种通用的数据交换格式,平台的无关性使得很多场合都需要用到XML。本文将详细介绍用Java解析XML的四种方法。 XML现在已经成为一种通用的数据交换格式,它的平台无关性,语言无关性,系统无关性,给数据集成与交互带来了极大的方便。对于XML本身的语法知识与技术细节,需要阅读相关的技术文献,这里面包括的内容有DOM(Document Object
  • spring中配置文件占位符的使用 avords
    1.类 <?xml version="1.0" encoding="UTF-8"?><!DOCTYPE beans PUBLIC "-//SPRING//DTD BEAN//EN" "http://www.springframework.o
  • 前端工程化-公共模块的依赖和常用的工作流 bee1314 webpack
    题记： 一个人的项目，还有工程化的问题嘛？   我们在推进模块化和组件化的过程中，肯定会不断的沉淀出我们项目的模块和组件。对于这些沉淀出的模块和组件怎么管理？另外怎么依赖也是个问题？ 你真的想这样嘛？   var BreadCrumb = require(‘../../../../uikit/breadcrumb’); //真心ugly。  
  • 上司说「看你每天准时下班就知道你工作量不饱和」，该如何回应？ bijian1013 项目管理沟通IT职业规划
    问题：上司说「看你每天准时下班就知道你工作量不饱和」，如何回应         正常下班时间6点，只要是6点半前下班的，上司都认为没有加班。   Eno-Bea回答，注重感受，不一定是别人的         虽然我不知道你具体从事什么工作与职业，但是我大概猜测，你是从事一项不太容易出现阶段性成果的工作
  • TortoiseSVN，过滤文件 征客丶 SVN
    环境： TortoiseSVN 1.8 配置： 在文件夹空白处右键 选择  TortoiseSVN -> Settings 在 Global ignote pattern 中添加要过滤的文件： 多类型用英文空格分开 *name ： 过滤所有名称为 name 的文件或文件夹 *.name ： 过滤所有后缀为 name 的文件或文件夹 --------
  • 【Flume二】HDFS sink细说 bit1129 Flume
    1. Flume配置   a1.sources=r1 a1.channels=c1 a1.sinks=k1 ###Flume负责启动44444端口 a1.sources.r1.type=avro a1.sources.r1.bind=0.0.0.0 a1.sources.r1.port=44444 a1.sources.r1.chan
  • The Eight Myths of Erlang Performance bookjovi erlang
    erlang有一篇guide很有意思： http://www.erlang.org/doc/efficiency_guide 里面有个The Eight Myths of Erlang Performance： http://www.erlang.org/doc/efficiency_guide/myths.html   Myth: Funs are sl
  • java多线程网络传输文件(非同步)-2008-08-17 ljy325 java多线程socket
    利用 Socket 套接字进行面向连接通信的编程。客户端读取本地文件并发送；服务器接收文件并保存到本地文件系统中。 使用说明:请将TransferClient, TransferServer, TempFile三个类编译，他们的类包是FileServer. 客户端: 修改TransferClient: serPort, serIP, filePath, blockNum,的值来符合您机器的系
  • 读《研磨设计模式》-代码笔记-模板方法模式 bylijinnan java设计模式
    声明： 本文只为方便我个人查阅和理解，详细的分析以及源代码请移步 原作者的博客http://chjavach.iteye.com/ import java.sql.Connection; import java.sql.DriverManager; import java.sql.PreparedStatement; import java.sql.ResultSet;
  • 配置心得 chenyu19891124 配置
    时间就这样不知不觉的走过了一个春夏秋冬，转眼间来公司已经一年了，感觉时间过的很快，时间老人总是这样不停走，从来没停歇过。 作为一名新手的配置管理员，刚开始真的是对配置管理是一点不懂，就只听说咱们公司配置主要是负责升级，而具体该怎么做却一点都不了解。经过老员工的一点点讲解，慢慢的对配置有了初步了解，对自己所在的岗位也慢慢的了解。 做了一年的配置管理给自总结下： 1.改变 从一个以前对配置毫无
  • 对“带条件选择的并行汇聚路由问题”的再思考 comsci 算法工作软件测试嵌入式领域模型
    2008年上半年，我在设计并开发基于”JWFD流程系统“的商业化改进型引擎的时候，由于采用了新的嵌入式公式模块而导致出现“带条件选择的并行汇聚路由问题”(请参考2009-02-27博文)，当时对这个问题的解决办法是采用基于拓扑结构的处理思想，对汇聚点的实际前驱分支节点通过算法预测出来，然后进行处理，简单的说就是找到造成这个汇聚模型的分支起点，对这个起始分支节点实际走的路径数进行计算，然后把这个实际
  • Oracle 10g 的clusterware 32位 下载地址 daizj oracle
    Oracle 10g 的clusterware 32位 下载地址 http://pan.baidu.com/share/link?shareid=531580&uk=421021908 http://pan.baidu.com/share/link?shareid=137223&uk=321552738 http://pan.baidu.com/share/l
  • 非常好的介绍：Linux定时执行工具cron dongwei_6688 linux
    Linux经过十多年的发展，很多用户都很了解Linux了，这里介绍一下Linux下cron的理解，和大家讨论讨论。cron是一个Linux 定时执行工具，可以在无需人工干预的情况下运行作业，本文档不讲cron实现原理，主要讲一下Linux定时执行工具cron的具体使用及简单介绍。 新增调度任务推荐使用crontab -e命令添加自定义的任务（编辑的是/var/spool/cron下对应用户的cr
  • Yii assets目录生成及修改 dcj3sjt126com yii
    assets的作用是方便模块化，插件化的，一般来说出于安全原因不允许通过url访问protected下面的文件，但是我们又希望将module单独出来，所以需要使用发布，即将一个目录下的文件复制一份到assets下面方便通过url访问。 assets设置对应的方法位置 \framework\web\CAssetManager.php   assets配置方法 在m
  • mac工作软件推荐 dcj3sjt126com mac
    mac上的Terminal + bash ＋ screen组合现在已经非常好用了，但是还是经不起iterm＋zsh＋tmux的冲击。在同事的强烈推荐下，趁着升级mac系统的机会，顺便也切换到iterm＋zsh＋tmux的环境下了。 我为什么要要iterm2 切换过来也是脑袋一热的冲动，我也调查过一些资料，看了下iterm的一些优点： * 兼容性好，远程服务器 vi 什么的低版本能很好兼
  • Memcached(三)、封装Memcached和Ehcache frank1234 memcachedehcachespring ioc
    本文对Ehcache和Memcached进行了简单的封装，这样对于客户端程序无需了解ehcache和memcached的差异，仅需要配置缓存的Provider类就可以在二者之间进行切换，Provider实现类通过Spring IoC注入。 cache.xml <?xml version="1.0" encoding="UTF-8"?>
  • Remove Duplicates from Sorted List II hcx2013 remove
    Given a sorted linked list, delete all nodes that have duplicate numbers, leaving only distinct numbers from the original list. For example,Given 1->2->3->3->4->4->5,
  • Spring4新特性——注解、脚本、任务、MVC等其他特性改进 jinnianshilongnian spring4
    Spring4新特性——泛型限定式依赖注入 Spring4新特性——核心容器的其他改进 Spring4新特性——Web开发的增强 Spring4新特性——集成Bean Validation 1.1(JSR-349)到SpringMVC  Spring4新特性——Groovy Bean定义DSL Spring4新特性——更好的Java泛型操作API  Spring4新
  • MySQL安装文档 liyong0802 mysql
      工作中用到的MySQL可能安装在两种操作系统中，即Windows系统和Linux系统。以Linux系统中情况居多。   安装在Windows系统时与其它Windows应用程序相同按照安装向导一直下一步就即，这里就不具体介绍，本文档只介绍Linux系统下MySQL的安装步骤。   Linux系统下安装MySQL分为三种：RPM包安装、二进制包安装和源码包安装。二
  • 使用VS2010构建HotSpot工程 p2p2500 HotSpotOpenJDKVS2010
    1. 下载OpenJDK7的源码：      http://download.java.net/openjdk/jdk7      http://download.java.net/openjdk/      2. 环境配置     ▶
  • Oracle实用功能之分组后列合并 seandeng888 oracle分组实用功能合并
    1       实例解析 由于业务需求需要对表中的数据进行分组后进行合并的处理，鉴于Oracle10g没有现成的函数实现该功能，且该功能如若用JAVA代码实现会比较复杂，因此，特将SQL语言的实现方式分享出来，希望对大家有所帮助。如下： 表test 数据如下： ID,SUBJECTCODE,DIMCODE,VALUE 1&nbs
  • Java定时任务注解方式实现 tuoni javaspringjvmxmljni
    Spring 注解的定时任务，有如下两种方式： 第一种： <?xml version="1.0" encoding="UTF-8"?> <beans xmlns="http://www.springframework.org/schema/beans"  xmlns:xsi="http
  • 11大Java开源中文分词器的使用方法和分词效果对比 yangshangchuan word分词器ansj分词器Stanford分词器FudanNLP分词器HanLP分词器
    本文的目标有两个： 1、学会使用11大Java开源中文分词器 2、对比分析11大Java开源中文分词器的分词效果 本文给出了11大Java开源中文分词的使用方法以及分词结果对比代码，至于效果哪个好，那要用的人结合自己的应用场景自己来判断。 11大Java开源中文分词器，不同的分词器有不同的用法，定义的接口也不一样，我们先定义一个统一的接口： /** * 获取文本的所有分词结果, 对比
按字母分类： ABCDEFGHIJKLMNOPQRSTUVWXYZ其他