浅显易懂的并查集简介 - 合并不相交的集合

前言

最近想了解一下并查集的概念，网上搜了很多资料都不满意，无意中看到一篇英文博客，写的非常浅显易懂，于是我花时间把它翻译成了中文，希望对想了解并查集的朋友有所帮助。想查看英文原版的朋友，可以直接移步：
https://www.hackerearth.com/zh/practice/notes/disjoint-set-union-union-find/ 。

简介

算法的效率有时会依赖于所使用的数据结构的效率。一个高效的数据结构可以减少算法的执行时间，而并查集就是这一类数据结构。

假设有一个集合，集合中包含N个元素，并且这个集合被分成若干子集。并查集被用来查询一个特定子集中每个元素之间的连通性，或者
各个子集之间的连通性。

这里给出一个例子：假设有5个人A，B，C，D和E。A是B的朋友，B是C的朋友，D是E的朋友。我们可以得到：

1. A，B和C是互相连通的。
2. D和E是互相连通的。

根据上面的推论，我们可以得到两个不相交的子集{A,B,C}和{D,E},并且可以用并查集来确定一个人与另一个人是否是连通（认识）的。

这里体现了并查集（Union Find）的两种主要操作：

1. Union(A,B)：连接元素A和B;
2. Find(A,B)：确认A与B是否连通。

另一个栗子：有一个集合S={0,1,2,3,4,5,6,7,8,9}，包含10个元素（即N=10）。我们可以使用一个数组Arr来管理各个元素之间的连通性。
Arr[]的大小为N，我们可以直接用集合S的元素作为索引来提取Arr[]中的数据（详见图例）。

假设：A和B是连通的，当且仅当Arr[A]=Arr[B]。

现在我们实现并查集的两种主要操作（如果看不懂可以直接看下面的栗子）：

1. Union(A,B)：与A连通的元素，其在Arr中的值都等于Arr[A]，与B连通的元素，其在Arr中的值都等于Arr[B]; 为了连接A和B，我们把所有Arr中所有等于Arr[A]的值改为Arr[B]。
2. Find(A,B)：检查是否Arr[A]=Arr[B]。

图例解析

刚开始的时候集合S中有10个子集，每个子集有单个元素，像下面这样：

相应的，数组Arr像下面这样：

现在执行操作Union(2,1)：

Arr变为：

接着执行操作Union(4,3)，Union(8,4)和Union(9,3)：

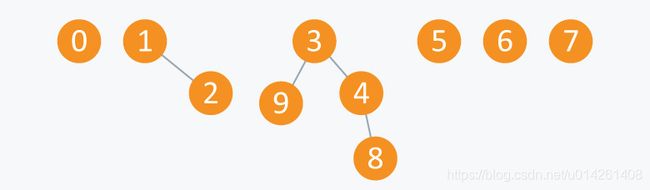
Arr变为：

执行操作Union(6,5)：

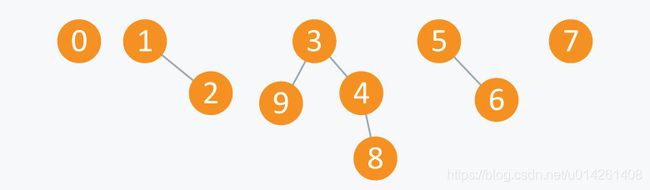
Arr变为：

在执行几个Union(A,B)操作之后，你可以看到S中有5个子集，分别为{3,4,8,9}，{1,2}，{5,6}，{0}和{7}。所有这些子集称为连通分量（Connected Component）。

从这里，我们可以看出并查集非常适用于图数据，例如连接节点，查找连通分量等等。

现在我们执行一些Find(A,B)操作：

1. Find(0,7)：0和7不连通，结果返回false。
2. Find(8,9)：8和9并不直接相连，但是存在一条路径连接8和9，因此结果返回true。

当我们从连通分量的角度看时：

1. Union(A,B)：合并两个包含A和B的连通分量;
2. Find(A,B)：确认A与B是否在同一个连通分量中。

因此，当我们执行操作Union(5,2)时，连通分量看起来像下面这样：

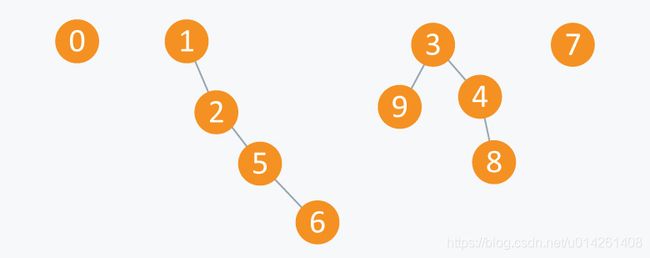
Arr变为：

代码实现

刚开始时有N个子集，每个子集包含单个元素，因此使用initialize()函数初始化：

void initialize( int Arr[ ], int N) {
    for(int i = 0;i

在union()函数中，连接两个元素需要遍历Arr[]。如果对所有元素执行union()操作，则时间复杂度为$O(N^2)$，效率比较低。

我们可以尝试另一种优化方案。

优化 1

主要思想：Arr[A]是A的父节点。

我们可以给每个子集设置一个根节点R，并且Arr[R]=R，即根节点的父节点是它自身。

为了解释优化算法，考虑一个集合S={0,1,2,3,4,5}。刚开始每个元素是它自己的根节点，即Arr[i]=i，可以表示为root(i)=i：

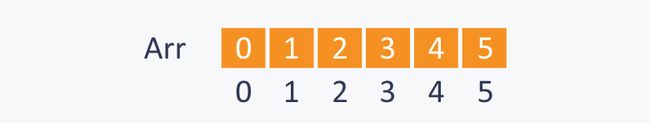
执行Union(1,0)之后，会把root(0)设置为root(1)的父节点。因为root(1)=1，root(0)=0，所以Arr[1]的值会从1变成0：

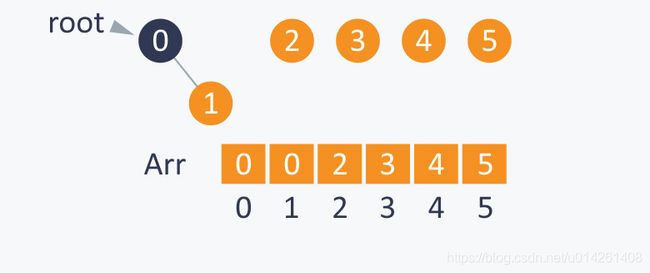
执行Union(0,2)之后，会把root(2)设置为root(0)的父节点，这一操作会间接地连通0和2。因为root(2)=2，root(0)=0，所以Arr[0]的值会从0变成2，子集{2,0,1}的根节点是2：

相似地，操作Union(3,4)会把root(4)设置为root(3)的父节点，Arr[3]的值会从3变成4，子集{3,4}的根节点是4：

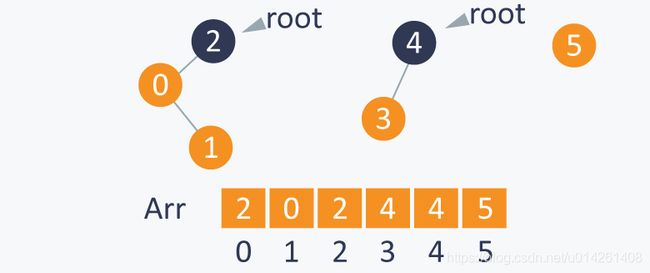
执行Union(1,4)之后，会把root(4)设置为root(1)的父节点。因为root(4)=4，root(1)=2，所以Arr[2]的值
会从2变成4，现在4变成了子集{0,1,2,3,4}的根节点：

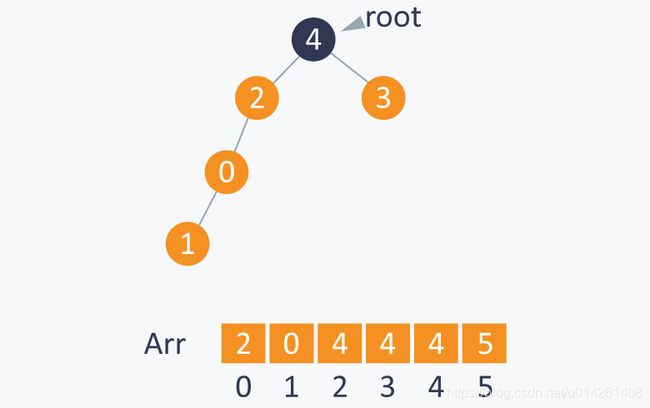
在执行了所有Union(A,B)的操作之后，我们可以通过Find(A,B)来查看A和B是否是连通的，即查看A和B的根节点是否相同。

那么问题来了，如何计算一个元素的根节点呢?

我们知道Arr[i]是元素i的父节点，那么i的根节点是Arr[Arr[...Arr[i]...]]]，我们可以循环查找i的父节点，直到找到一个元素k，k的父节点是它自己，那么k就是i的根节点。

注意：只有在子集的元素之间不存在环时才可使用循环查找。

1. Find(1,4)：1和4有相同的根节点4，结果返回true。
2. Find(3,5)：3的根节点root(3)=4，而5的根节点root(5)=5，因此结果返回false。

实现：

前文代码中初始化函数initialize()不变。

//finding root of an element.
int root(int Arr[ ],int i){
    //chase parent of current element until it reaches root.
    while(Arr[ i ] != i) {
        i = Arr[ i ];
    }
    return i;
}

/*modified union function where we connect the elements by changing the root of one of the element */
int union(int Arr[ ] ,int A ,int B){
    int root_A = root(Arr, A);       
    int root_B = root(Arr, B);  
    //setting parent of root(A) as root(B).
    Arr[ root_A ] = root_B ;  
}

bool find(int A,int B){
    //if A and B have same root,means they are connected.
    if( root(A)==root(B) )       
        return true;
    else
        return false;
}

如你所见，连接两个元素的union()函数，其时间复杂度为$O(N)$。最坏情况下，本算法的运算时间相当于上文的遍历算法。
另一个缺点是，我们在连接两个子集时并没有检查哪个子集里的元素比较多。因此root()函数在最坏情况下也会遍历整个数组。

我们可以避免这种情况！现在我们记录每个子集的元素个数，在连接两个元素时，我们总是将元素个数比较少的子集的根连接到元素个数较多的子集根节点上。

优化 2

栗子：

如下图所示，如果需要执行操作Union(1,5)，我们连接子集A（包含1）的根到子集B（包含5）的根上，因为子集A包含的元素更少。

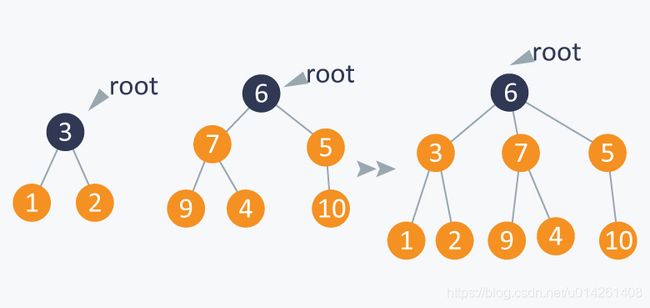
通过这些合并操作，我们最后会得到一棵平衡树。这些操作称为带权重的合并（weighted_union）操作。

实现：

初始化时，前文的initialize()函数运行逻辑不变，我们现在要添加一个数组size[]来记录每个子集的大小：

//modified initialize function:
void initialize( int Arr[ ], int N){
    for(int i = 0;i

前文中root()和find()函数保持不变。

现在我们要根据元素的个数来连接两个子集，修改union()函数如下：

void weighted-union(int Arr[ ],int size[ ],int A,int B){
    int root_A = root(A);
    int root_B = root(B);
    if(size[root_A] < size[root_B ]){
        Arr[ root_A ] = Arr[root_B];
        size[root_B] += size[root_A];
    }
    else{
        Arr[ root_B ] = Arr[root_A];
        size[root_A] += size[root_B];
    }
}

栗子：

我们给定集合S={0,1,2,3,4,5}：初始化时共6个子集，每个子集有单个元素，每个元素的根是它自身。size[]数组长这样：

执行Union(0,1)，因为包含0和1的两个子集大小相同，因此连接的次序可以随意。假设连接之后，0变成1的根节点，则相应的size[0]从1变成2：

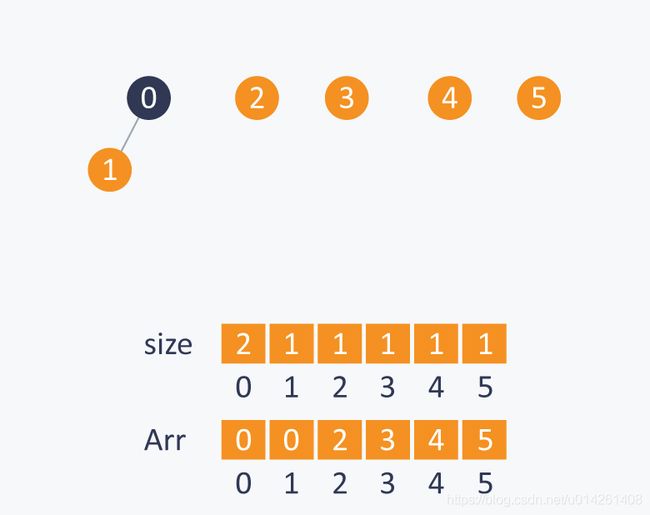
在执行Union(1,2)时，我们连接root(2)到root(1)，因为包含2的子集更小：

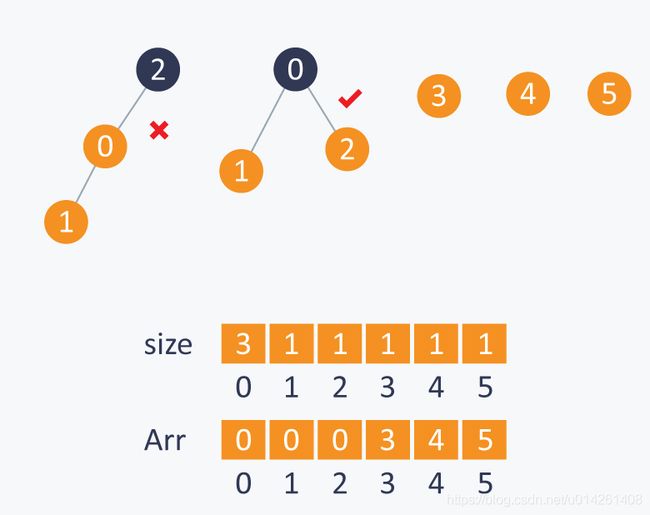
相似地，在执行Union(3,2)时，我们连接root(3)到root(2)，因为包含3的子集更小：

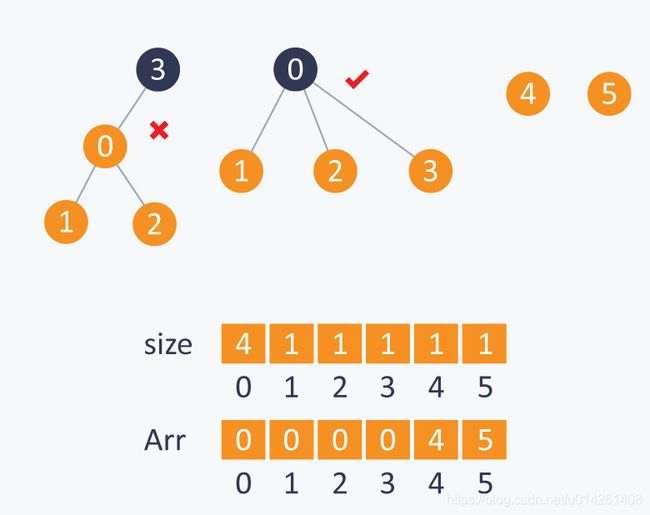
如上所述，通过维持一棵平衡树，我们将union和find的时间复杂度从$O(N)$降至$O(lo{g}_{2}N)$。

我们还能做得更好吗？

优化 3

路径压缩：当计算A的根节点时，设置元素i指向其祖父节点（因此可以将路径长度减半），其中i是在运行root(A)时经过的中间节点。

// modified root function.
int root (int Arr[ ] ,int i){
    while(Arr[ i ] != i){
        Arr[ i ] = Arr[ Arr[ i ] ] ; 
        i = Arr[ i ]; 
    }
    return i;
}

当我们同时使用带权重的合并和路径压缩技术时，每一个union_find操作的时间复杂度为$O(log\ast (N))$，其中N是集合中元素的总个数。

注：$O(log\ast (N))$为$O[log(log(...log(N)))]$的简写，意为重复$log$许多次直到把N缩减为小于等于1。

例如$N=2^{65536}$，则$O(log\ast (N))=5$，意为重复5次$log$，即进行5次迭代。$O(log\ast (N))$增长极度缓慢，远比$log(N)$优秀，全宇宙中的原子数目也不过$N=2^{65536}$（数据未经证实hahaha）。

应用

1. 如前所述，并查集可以用来确定图中的连通分量。我们可以利用并查集来确定是否两个节点在同一个连通分量中。通过带权重的合并操作和路径优化技术，我们可以把并查集的时间复杂度优化到极致，因此在一个非常大且密集的图里，并查集也是一个表现非常优秀的数据结构。
2. 并查集可以用来检测图中的环。当往图里添加一条边时，我们可以通过并查集来确定是否该操作会在图中形成环。在计算最小生成树的Kruskal算法中，我们可以用并查集来查找环，以此来加快算法的执行速度。