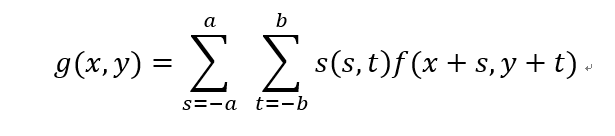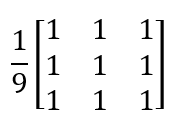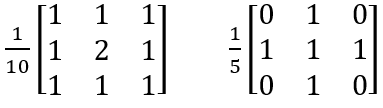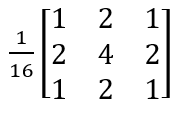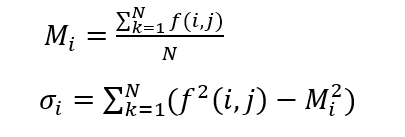图像处理之图像预处理
在对图像进行边缘检测、分割等操作之前,都要对原始的图像进行增强处理,从而消除无关信息,改善图像效果,突出图像特征,便于计算机进行识别和分析。
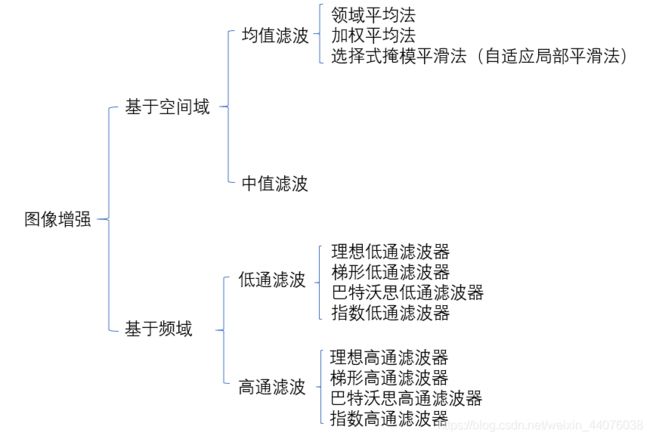
根据图像处理所在空间的不同,可以分为基于空间域的增强方法和基于频率域的增强方法,空间域即图像本身,这种方法直接对图像的像素进行处理,频率域则是以修改图像的傅里叶变换为基础。
一、空间滤波
空间滤波是采用滤波进行图像增强,以卷积运算为基础。目的是去除高频噪声,边缘增强、线性增强、去模糊等。
如图所示,空间滤波主要包括三个步骤:
1)建立掩模
2)再图像上逐点移动掩模
3)在每一点进行卷积运算,R=w(-1,-1)f(x-1,y-1)+w(-1,0)f(x-1,y)+......+w(1,1)f(x+1,x+1)
| f(x-1,y-1) | f(x-1,y) | f(x-1,y+1) |
| f(x,y-1) | f(x,y) | f(x,y+1) |
| f(x+1,Y-1) | f(x+1,y) | f(x+1,y+1) |
模板对应的图像像素
| w(-1,-1) | w(-1,0) | w(-1,1) |
| w(0,-1) | w(0,0) | w(0,1) |
| w(1,-1) | w(1,0) | w(1,1) |
模板系数
在M*N的图像f上,用m*n的滤波器进行线性滤波的公式如下:
其中m=2a+1,n=2b+1,a,b为非负整数,x=0,1,2,...,M-1,y=0,1,2,...,N-1.
1、均值滤波
(1)领域平均法
最简单的平滑滤波是将原图的像素和周围的8个像素灰度值相加求平均值(除以9)作为新图中该像素的灰度值。领域平均法的模板为:
在实际应用中,可以根据不同需要选择不同尺寸的模板,如3x3,5x5,7x7等。领域平均法是以图像模糊为代价降低噪声的,模板尺寸越大,噪声降低越明显,图像越模糊。其原理是:假设(i,j)是噪声点,其灰度与相邻像素相差很大,采用领域平均法就是用领域的平均值来代替它,从而起到平滑的作用。
(2)加权平均法
对于同一尺寸的模板,可以根据不同的位置选择不同的数值。一般来说,离中心像素越近的点对滤波贡献较大,所以权重较大,离中心像素越远权重越小。通常取模板周边最小的系数为1,内部的系数成比例增加,中心系数最大。常用的模板有:
还有一种是根据二维高斯分布来确定各个系数值,称为高斯模板。
与领域平均法相比,加权平均法使得掩模中心位置的像素比其他位置的像素权重要大,使得距离中心较远的点贡献度降低,减小了平滑带来的模糊效应,使得图像的边缘要相对清晰一点。在实际应用中,可以根据图像结构确定模板,使得加权值成为自由调节的参数,应用比较灵活。但是由于模板不能分解,所以计算效率不高。
(3)选择式掩模平滑法(自适应局部平滑法)
该算法也是以模板运算为基础,下面以5x5模板窗口为例子。首先制作下面9种模板。
9种模板
以中心像素(i,j)为基准点,分别计算每个模板下窗口内的平均值和方差。
其中N为掩模对应的像素个数。
由于含有边沿的区域,方差比平缓区域大,所以用方差最小条件下的的模板进行平均化。这样在滤波的同时不会破坏边缘的细节。克服了领域平均法和加权平均法在消除噪声同时所存在的平均化的缺陷。
2、中值滤波
中值滤波一般采用含有奇数个点的滑动窗口,用窗口中各个像素点灰度值的中值来代替制定点的灰度。中值滤波也是一种典型的低通滤波,主要用来抑制脉冲噪声,能够彻底消除尖波干扰,也能很好的保护图像边缘。但是对于点线等细节太多的图像不合适。
中值滤波过程(205为中值)
中值滤波的计算在于滑动窗口内像素的排序。较快的排序法是冒泡排序法,假设窗口内有m个像素,那么每个窗口需要做
m(m-2)/2次比较。这种做法包含了大量重复计算,比较费时。可以通过快速并行的中值滤波方法,避免大量重复比较。
(==未完待续==)