【专题总结】 网络流
day1 (最大流)
一、问题导向:
1)有网络模型
2)问题的可行性
3)n^2迷之复杂度
二、模板理解
1)EK算法
一个基础:增广路。
只要能实现更正之前的操作,枚举完所有情况得到的一定是最优解(之一)
更正实现:建立反向弧(增减与原边相反的反向边)
e[1]== u->v c(capacity)
e[2]== v->u 0
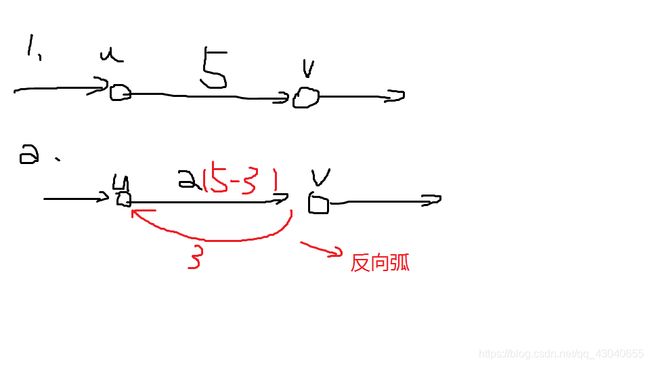
为何反向弧能实现更改?
可以和匈牙利算法相比较。 匈牙利直接修改之前的情况,每一种方案可看成左右两个点连接一条边,只用修改一条边,O(1)!

但网络中的方案远不止一条边,所以直接修改时间空间复杂度都很高。
其他的点反着走一遍,相当于抵消了正着的流量。
所以增加反向弧,修改的过程就是走一遍的过程。
(自己举个例子看一看)
EK算法:
由于是bfs,不能分叉
struct edge{
int u,v,nxt,c,f;
}e[maxm];
int head[maxn],cnt=1;
int n,m;
int S,T;
int path[maxn];
int a[maxn];
inline void diadd(int u,int v,int c){
e[++cnt]=(edge){u,v,head[u],c,0};
head[u]=cnt;
e[++cnt]=(edge){v,u,head[v],0,0};
head[v]=cnt;
}
inline int BFS(int s,int t){
memset(a,0,sizeof a);
memset(path,-1,sizeof path);
//path记录前驱边
//a记录当前点可以获得的最大流量(也可以判断是否访问过)
queue <int> q;
q.push(s);
a[s]=InF;
while(!q.empty()){
int u=q.front();q.pop();
for(int i=head[u];i;i=e[i].nxt){
edge x=e[i];
if(!a[x.v]&&x.f<x.c){
path[x.v]=i;
a[x.v]=min(a[u],x.c-x.f);
q.push(x.v);
}
}
if(a[t])return a[t];
}
return 0;
}
inline int EK(int s,int t){
int flow=0;
while(1){
int tmp=BFS(s,t);
if(!tmp)break;//如果更新不动了,就break(无法继续增广)
for(int i=t;i!=s;i=e[path[i]].u){
e[path[i]].f+=tmp;
e[path[i]^1].f-=tmp;
}
flow+=tmp;
}
return flow;
}
dinic:
每一次做都先把图分层
相当于用dep(层次),同层跳过,优化了EK的同层多余枚举
此时dfs要先求出可流通的最大值,再加减(回溯)、
相当于"分叉"
inline bool BFS(){
queue <int>q;
q.push(S);
//memset(dep+1,-1,n<<2);//源点标记为0
for(int i=0;i<=n;++i)dep[i]=-1;
dep[S]=0;
while(!q.empty()){
int u=q.front();q.pop();
for(int i=head[u];i;i=e[i].nxt){
edge x=e[i];
if(x.c>0&&dep[x.v]==-1){
dep[x.v]=dep[u]+1;
if(x.v==T)return 1;
q.push(x.v);
}
}
}
return 0;
}
int DFS(int u,int f){
if(u==T||f==0)return f;
int out=0;//当前成功流出的流量
for(int &i=cur[u];i;i=e[i].nxt){//&: 当前弧优化
int v=e[i].v,&c=e[i].c;
if(e[i].c&&dep[v]==dep[u]+1){
int w=DFS(v,min(c,f));
if(!w)continue;
f-=w,out+=w;
c-=w,e[i^1].c+=w;
if(f==0)break;//很重要,这样当前可用弧的优化才正确
}
}
if(!out)dep[u]=-1;
//减枝,相当于这个点不能流入源点就舍弃
return out;
}
inline int dinic(){
int mflow=0;
while(BFS()){
for(int i=0;i<=n;++i)cur[i]=head[i];
//源点是0
mflow+=DFS(S,INF);
}
return mflow;
}
建图:
1.和二分图类比
用入点,出点流量控制“每一个点只能被匹配一次“
例题:
woj#2303 「网络流 24 题」搭配飞行员
描述
飞行大队有若干个来自各地的驾驶员,专门驾驶一种型号的飞机,这种飞机每架有两个驾驶员,需一个正驾驶员和一个副驾驶员。由于种种原因,例如相互配合的问题,有些驾驶员不能在同一架飞机上飞行,问如何搭配驾驶员才能使出航的飞机最多呢?
P.S.因为驾驶工作分工严格,两个正驾驶员或两个副驾驶员都不能同机飞行。
2<=n<=100;
#include2.拆点(控制“点”的使用(进入)限制)
例题:
#2351 [USACO07OPEN]吃饭Dining
描述
农夫JOHN为牛们做了很好的食品,但是牛吃饭很挑食. 每一头牛只喜欢吃一些食品和饮料而别的一概不吃.虽然他不一定能把所有牛喂饱,他还是想让尽可能多的牛吃到他们喜欢的食品和饮料.
农夫JOHN做了F (1 <= F <= 100) 种食品并准备了D (1 <= D <= 100) 种饮料. 他的N (1 <= N <= 100)头牛都以决定了是否愿意吃某种食物和喝某种饮料. 农夫JOHN想给每一头牛一种食品和一种饮料,使得尽可能多的牛得到喜欢的食物和饮料.
每一件食物和饮料只能由一头牛来用. 例如如果食物2被一头牛吃掉了,没有别的牛能吃食物2.
#include