TOYS POJ - 2318（计算几何向量叉乘）

POJ—2318
Calculate the number of toys that land in each bin of a partitioned toy box.
Mom and dad have a problem - their child John never puts his toys away when he is finished playing with them. They gave John a rectangular box to put his toys in, but John is rebellious and obeys his parents by simply throwing his toys into the box. All the toys get mixed up, and it is impossible for John to find his favorite toys.

John’s parents came up with the following idea. They put cardboard partitions into the box. Even if John keeps throwing his toys into the box, at least toys that get thrown into different bins stay separated. The following diagram shows a top view of an example toy box.

For this problem, you are asked to determine how many toys fall into each partition as John throws them into the toy box.
Input
The input file contains one or more problems. The first line of a problem consists of six integers, n m x1 y1 x2 y2. The number of cardboard partitions is n (0 < n <= 5000) and the number of toys is m (0 < m <= 5000). The coordinates of the upper-left corner and the lower-right corner of the box are (x1,y1) and (x2,y2), respectively. The following n lines contain two integers per line, Ui Li, indicating that the ends of the i-th cardboard partition is at the coordinates (Ui,y1) and (Li,y2). You may assume that the cardboard partitions do not intersect each other and that they are specified in sorted order from left to right. The next m lines contain two integers per line, Xj Yj specifying where the j-th toy has landed in the box. The order of the toy locations is random. You may assume that no toy will land exactly on a cardboard partition or outside the boundary of the box. The input is terminated by a line consisting of a single 0.
Output
The output for each problem will be one line for each separate bin in the toy box. For each bin, print its bin number, followed by a colon and one space, followed by the number of toys thrown into that bin. Bins are numbered from 0 (the leftmost bin) to n (the rightmost bin). Separate the output of different problems by a single blank line.
Sample Input
5 6 0 10 60 0
3 1
4 3
6 8
10 10
15 30
1 5
2 1
2 8
5 5
40 10
7 9
4 10 0 10 100 0
20 20
40 40
60 60
80 80
5 10
15 10
25 10
35 10
45 10
55 10
65 10
75 10
85 10
95 10
0
Sample Output
0: 2
1: 1
2: 1
3: 1
4: 0
5: 1

0: 2
1: 2
2: 2
3: 2
4: 2
Hint
As the example illustrates, toys that fall on the boundary of the box are “in” the box.

题意
有一个玩具盒，被n个隔板分开成左到u右n+1个区域，然后给每个玩具的坐标，求每个区域有几个玩具。

题解
依次用叉积判断玩具在每个隔板左边还是右边。

知识

设a⃗ =(x1,y1),b⃗ =(x2,y2)。

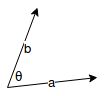
点乘：内积（数量积），a⃗ ⋅b⃗ =|a||b|cosθ=x1⋅x2+y1⋅y2

叉乘：外积（向量积），|c⃗ |=|a⃗ ×b⃗ |=|a||b|sinθ=x1⋅y2−x2⋅y1

向量积的结果是一个向量，方向用“右手法则”判断（四指为a的方向，朝手心方向摆动到b的方向，大拇指就是c的方向）

几何意义：

点乘的几何意义是：是一条边向另一条边的投影乘以另一条边的长度

叉乘的几何意义是：两个矢量围成的平行四边形的面积

代码一：

#include 
#define N 50001
int n,m;
int x1,y1,x2,y2,u[N],l[N];
int ans[N];
int xmul(int x1,int y1,int x2,int y2){
    return (x1*y2)-(x2*y1);
}
int main(){
    while(scanf("%d",&n),n){
        scanf("%d%d%d%d%d",&m,&x1,&y1,&x2,&y2);
        for(int i=0;i<n;++i)
            scanf("%d%d",u+i,l+i),ans[i]=0;
        ans[n]=0;
        for(int i=0,j,x,y;i<m;++i){
            scanf("%d%d",&x,&y);
            for(j=0;j<n;++j)
                if(xmul(x-l[j],y-y2,u[j]-l[j],y1-y2)<=0)
                    break;
            ++ans[j];
        }
        for(int i=0;i<=n;++i)
            printf("%d: %d\n",i,ans[i]);
        puts("");
    }
}

代码二：

#include 
#include 
#include 
using namespace std;
typedef long long ll;
const int maxn=5e3+10;
 
ll up[maxn],down[maxn],x[maxn],y[maxn];
int ans[maxn];
ll x1,x2,y1,y2;
int n,m;
 
ll getval(ll x1,ll y1,ll x2,ll y2)
{
    return x1*y2-x2*y1;
}
 
int judge(ll xx,ll yy,int pos)
{
    ll res1,res2;
    res1=getval(xx-down[pos],yy-y1,up[pos]-down[pos],y2-y1);
    res2=getval(xx-down[pos+1],yy-y1,up[pos+1]-down[pos+1],y2-y1);
    if(res1*res2<0) return 0;
    else{
        if(res1<0) return -1;
        else return 1;
    }
}
 
int main()
{
    int i,l,r,mid,res,p;
    while(scanf("%d",&n)!=EOF){
        if(n==0) break;
        scanf("%d%lld%lld%lld%lld",&m,&x1,&y1,&x2,&y2);
        swap(y1,y2);
        up[0]=x1,down[0]=x1;
        up[n+1]=x2,down[n+1]=x2;
        for(i=1;i<=n;i++){
            scanf("%lld%lld",&up[i],&down[i]);
        }
        for(i=1;i<=m;i++){
            scanf("%lld%lld",&x[i],&y[i]);
        }
        for(i=0;i<=n;i++) ans[i]=0;
        for(i=1;i<=m;i++){
            if(x[i]==x1) ans[0]++;
            else if(x[i]==x2) ans[n]++;
            else{
                l=0,r=n;
                while(l<=r){
                    mid=(l+r)/2;
                    res=judge(x[i],y[i],mid);
                    if(res==0){
                        p=mid;
                        break;
                    }
                    else if(res==-1) r=mid-1;
                    else l=mid+1;
                }
                ans[p]++;
            }
        }
        for(i=0;i<=n;i++){
            printf("%d: %d\n",i,ans[i]);
        }
        printf("\n");
    }
    return 0;
}