线性代数与matlab中方程组求解

摘要

之前已经发布过几篇线性代数相关知识的文章作为学习matlab方程组求解的前期知识铺垫。如果对线性代数知识还不是比较熟悉，可以参考一下文章：
[补充内容]关于使用matlab进行方程组求解的线性代数相关知识补充——行列式
[补充内容]关于使用matlab进行方程组求解的线性代数相关知识补充——矩阵
[补充内容]关于使用matlab进行方程组求解的线性代数相关知识补充——n维向量
[补充内容]关于使用matlab进行方程组求解的线性代数相关知识补充——线性方程组
[补充内容]关于使用matlab进行方程组求解的线性代数相关知识补充——特征值与特征向量
[补充内容]关于使用matlab进行方程组求解的线性代数相关知识补充——二次型
本文会包含大量的个人观念及看法，由于本人非数学专业出身，查阅的资料未必全是正确的，自己的观点也不可能不会出错。如在在理论观点上有论述错误，欢迎斧正！！！

数组与矩阵

matlab中无论是多项式、方程组，它的系数都存在矩阵当中。但在matlab中两者的格式很相似，但这俩确实不是一个东西。
数组全称数组数据结构，实际的作用是存储数据，作用类似于一个表格。
矩阵是由m行n列排列组成的矩形阵列，用于存储数字、符号、表达式。
两者比较不难看出区别，数组涵盖的范围更广，数组可以存储非数字、符号、表达式的内容，例如字符串等。但对存储数字、符号、表达式而言，两者应该可以近似等同，二维数组就可以被称为矩阵。

多项式？方程组？

多项式的系数也是放在矩阵当中的，但是要注意多项式之间的转化应该是这样子的：

因为matlab中数据以数组方式存储，所以才会以这种形式输入各项系数。第二个矩阵中虽然有五个元素，但实际上都是x，是一个变量。
方程组则是这样的：

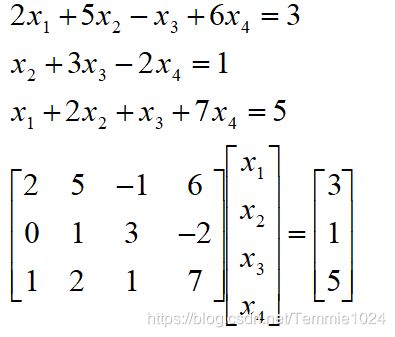
这里面x₁x₂x₃x₄就是不同的变量。
在输入你的数组时想明白你到底是在计算多项式还是方程组

matlab中特有的左除 \

平时除法计算用的是/右除号，被除数a在左，除数b在右，写作a/b；左除是除数在左，被除数在右，写作b\a等价于a/b。
个人认为添加左除的目的是方便简化软件的计算过程，对于方程组而言，它的系数组成了一个矩阵，而对矩阵的乘除，位置不同，结果也不同，因此除也变成了左右之分，对于一个含有一个未知数的方程而言左除右除没有区别，但对于矩阵来讲就有所差异了。

一些线性方程组的名词

对于方程组个数与未知数个数的比较，方程组分为了以下三类
方阵方程组：当未知数与方程个数相等时（就是n行n列，必须为方阵）
     非奇异系数矩阵：系数矩阵满秩，意味着有唯一解（唯一解的条件是方程的增广矩阵[A|b]的秩=[A]的秩，即：r(A)=r($\overline{\text{A}}$)=n，A已经满秩，所以非奇异系数矩阵所构成的方程必有唯一解）。
     奇异系数矩阵：系数矩阵不满秩，意味着有无穷多解或者无解，这取决于增广矩阵与系数矩阵的秩的关系（若r(A)≠r($\overline{\text{A}}$)则无解，若r(A)=r($\overline{\text{A}}$)）。
超定方程组：当未知数小于方程个数时（这种情况依旧要根据秩进行分析，若r(A)=r($\overline{\text{A}}$)=n则有唯一解；若r(A)≠r($\overline{\text{A}}$)则无解；若r(A)=r($\overline{\text{A}}$)）
欠定方程组：当未知数大于方程个数时，显然解不唯一。

matlb是怎样表示线性方程组的？

首先，先了解线性方程组的概念：线性方程组是各个方程关于未知量均为一次的方程组。
在线性代数的学习中，我们解到线性方程组中包含线性齐次方程组AX=0与线性非齐次方程组AX=b,
根据矩阵的乘法，上面的方程组与下面的矩阵形式等价。

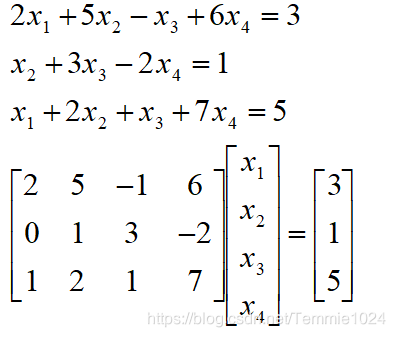
方程组解法

对于AX=0的线性其次方程，只需要使用null函数就可以求解

接下来主要介绍非齐次方程的特解求法：
对应前面讲到的三种解的情况以及未知数与方程个数的情况，将解决方法分为下面几种。

秩的关系\未知数与方程关系	相等（方阵）	小于（超定）	大于（欠定）
r(A)=r($\overline{\text{A}}$)=n唯一解	非奇异 x=A\b	你添加了可消去的方程	不存在
r(A)≠r($\overline{\text{A}}$)无解	奇异	x=A\b但结果是最小二乘解	无解
r(A)=r($\overline{\text{A}}$)	奇异，x= pinv(A)*b	你添加了可消去的方程	x=A\b求得最小范数解

注意：对于非奇异矩阵使用的A\b若用在奇异矩阵上会出现警告。
   pin(A)是指A的伪逆，因为可逆意味着矩阵对应的行列式的值不等于0，即矩阵满秩。
   对于方阵奇异无穷多解的情况，还分有精确解与无精确解，无精确解的方程组结果是通过最小二乘法找到的最接近原方程结果的值。验证解是否是精确解可以通过A*pinv(A)*b是否能重新返回b的值来判断，能返回就是精确值，否则就是无精确。
   这里面超定方程的范围要比一般定义的广泛，超定方程组的定义：是指方程个数大于未知量个数的方程组;我显然把重复的方程也算在了其中，而这些方程有些时候是可以在输入前化简掉的。考虑到有时候列式化简未必能做到完全，所以我也把这类放到了超定方程组里进行讨论。（也就是说，一般的超定方程组是存在矛盾方程一般是在进行拟合时才会出现的，因为拟合曲线不能完全与原曲线重合，出现了一些点并不在方程上的现象，所以会有矛盾。）
   最小范数解应该就是指在这无穷多的结果中以向量表示最小的解。（大概，这个定义看完有点蒙）
另外，对于系数矩阵的解法，matlab也提供了相应的函数，这里不在说明，详见帮助。

matlab中求解的实际效果

根据上面所讲，我编写了一个名为 LEC 的线性非齐次方程组运算函数。.m文件我也上传了，需要的自取。
LEC函数文件
A与A|b秩的计算文件

	[rankA,rankAB]=rank_test(A,b)
	[c1,result,conlusion]=LEC(A,b)

function [conclusion,result,c1] = LEC(A,b)
%UNTITLED 此处显示有关此函数的摘要
%   此处显示详细说明
ra=rank(A);%系数矩阵的秩
ra1=rank([A,b]);%增广矩阵的秩
[m,n]=size(A);%求出系数矩阵的行列值，列数=未知数个数
if m==n
    c1='方程组为方阵方程组';
    if (ra==n&&ra1==n)
        result=A\b;
        conclusion='方程有唯一解';
    elseif ra~=ra1
      	result=pinv(A)*b;
        conclusion='方程无解,但通过最小二乘法可以获得非精确解';
    else
        result=pinv(A)*b;
        conclusion='方程有无穷解，但有精确解';
    end
elseif m>n
    c1='方程组为超定方程组或含有多余方程';
    if (ra==n&&ra1==n)
        result=A\b;
        conclusion='含有多余方程,方程有唯一解';
    elseif ra~=ra1
      	result=A\b;
        conclusion='方程组有最小二乘解';
    else
        result=pinv(A)*b;
        conclusion='含有多余方程,方程有无穷解，但有精确解';
    end
else
    c1='方程组为欠定方程组';
    if (ra==n&ra1==n)
        result='错误';
        conclusion='怎么可能出现这个结果';
    elseif ra~=ra1
      	result='无解';
        conclusion='方程无解';
    else
        result=A\b;
        conclusion='方程有无穷解，此结果为最小范数解';
    end
end

根据帮助文档中以及自己编写的例子，我们将数据输入，查看运行效果是否与结论一致。
方阵唯一解

	x1=3 x2=4 x3=6 编写方程
	A=[1 1 1;1 2 0;7 1 -4];b=[13;11;1];

我们先来检查一下秩的条件是否满足

调用函数运算，结果一致。

方阵无解
使用帮助文档给的例子

具体的数值如下

	A=[1 3 7;-1 4 4;1 10 18];b=[3;6;0];

验证秩是否满足条件

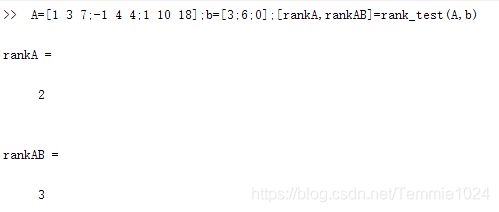
运行结果(帮助中没有给出实际结果，而是向下求了一步，我也同样添加这一步)结果一致


方阵无穷解
使用帮助文档给的例子

具体数值如下

	A=[1 3 7;-1 4 4;1 10 18];b=[5;2;12];

验证秩是否满足条件

运行结果

与帮助答案一致。

超定唯一解

	x1=3 x2=4 x3=6 编写方程
	A=[1 1 1;1 2 0;7 1 -4;2 2 2];b=[13;11;1;26];

我们先来检查一下秩的条件是否满足

运行结果，与设定答案一致

超定无解
使用帮助的例子

具体数据如下

	A=[1 1;1 0.7408;1 0.4493;1 0.3329;1 0.2019;1 0.1003];b=[0.82;0.72;0.63;0.6;0.55;0.5];

我们先来检查一下秩的条件是否满足

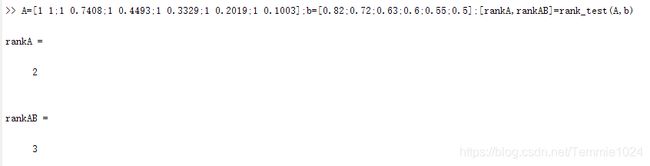
运行结果，与答案相差0.0001应该为计算精度或者进借位的原因


超定无穷解

	将方阵无穷解添加一行线性相关的方程
	A=[1 3 7;-1 4 4;1 10 18;2 6 14];b=[5;2;12;10];

我们先来检查一下秩的条件是否满足

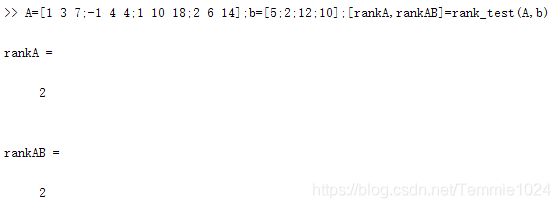
运行结果，一致，虽然加了一行，但在程序中所走的路线完全不同。

欠定无穷解
使用帮助的例子

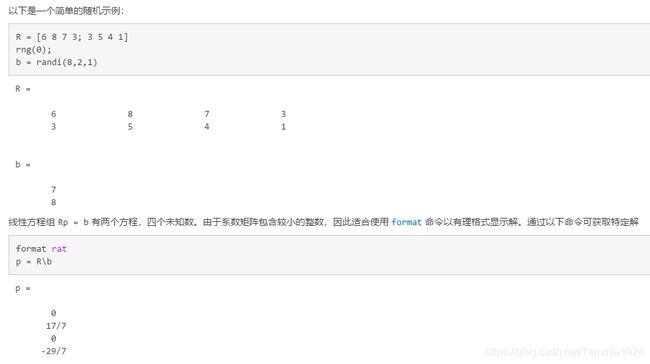
具体数据如下

	A=[6 8 7 3;3 5 4 1];b=[7;8];

这个例子可以很容易看出秩的关系，这里不在通过程序验证
运行结果，因为程序中未设置显示格式，默认显示为小数，实际结果一致。