MATLAB数据分析与多项式计算

1.

对多项式f(x)与g(x)做加、减、乘、除运算，并计算它们的商的导函数。

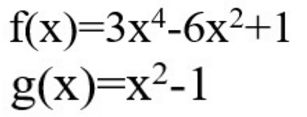
>> f=[3,0,-6,0,1];g=[1,0,-1];g1=[0,0,g];
>> f+g1    %加
ans =
     3     0    -5     0     0
>> f-g1    %减
ans =
     3     0    -7     0     2
>> conv(f,g)  %乘
ans =
     3     0    -9     0     7     0    -1
>> [Q,r]=deconv(f,g)  %商和余数
Q =
     3     0    -3
r =
     0     0     0     0    -2
>> conv(g,Q)+r
ans =
     3     0    -6     0     1
>> [p,q]=polyder(f,g)  %多项式导数
p =
     6     0   -12     0    10     0
q =
     1     0    -2     0     1

2.

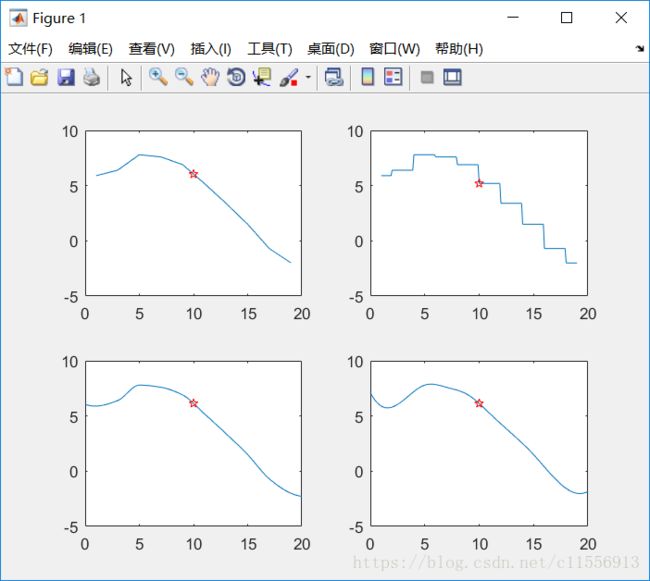
在某未知函数关系中，y值随x值的变化而变化。已知当x取值为[1，3，5，7，9，11，13，15，17，19]时，y的取值为[5.9，6.4，7.8，7.6，6.9，5.2，3.4，1.5，-0.7，-2]，用四种数据插值的方法估算当x取值为10时y的值。

x=[1,3,5,7,9,11,13,15,17,19];
y=[5.9,6.4,7.8,7.6,6.9,5.2,3.4,1.5,-0.7,-2];
x1=0:0.1:20;
y1=interp1(x,y,x1,'linear');  %线性插值
subplot(2,2,1)
a=find(x1==10);
y1(a)
plot(x1,y1,x1(a),y1(a),'rp')
y2=interp1(x,y,x1,'nearest');  %最近点插值
subplot(2,2,2)
b=find(x1==10);
y2(b)
plot(x1,y2,x1(b),y2(b),'rp')
y3=interp1(x,y,x1,'pchip');  %分段3次埃尔米特插值
subplot(2,2,3)
c=find(x1==10);
y3(c)
plot(x1,y3,x1(c),y3(c),'rp')
y4=interp1(x,y,x1,'spline');  %3次样条插值
subplot(2,2,4)
d=find(x1==10);
y4(d)
plot(x1,y4,x1(d),y4(d),'rp')

四种不同的方式结果如下：
ans =
    6.0500

ans =
    5.2000

ans =
    6.1446

ans =
    6.1361

3.

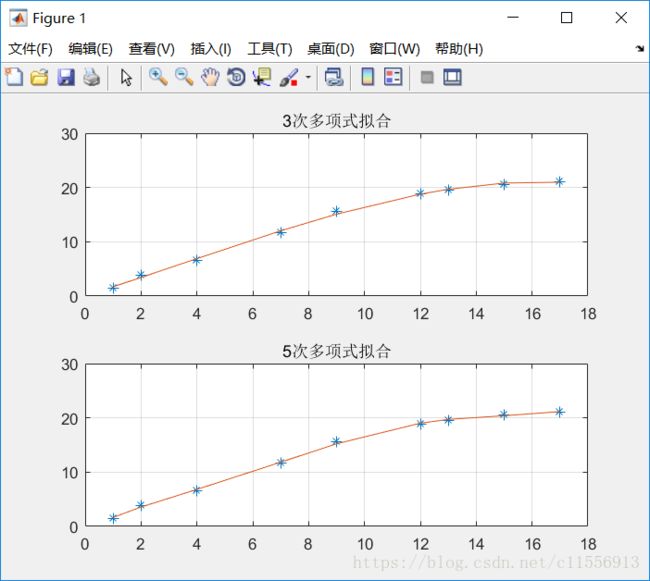
已知向量x和y，其中x=[1，2，4，7，9，12，13，15，17]，y=[1.5，3.9，6.6，11.7，15.6，18.8，19.6，20.6，21.1]，y值随x值的变化而变化。请分别用3次和5次多项式进行拟合，并绘制拟合曲线。

x=[1,2,4,7,9,12,13,15,17];
y=[1.5,3.9,6.6,11.7,15.6,18.8,19.6,20.6,21.1];
p=polyfit(x,y,3);
subplot(2,1,1)
plot(x,y,'*',x,polyval(p,x))
title('3次多项式拟合')
grid on
p=polyfit(x,y,5);
subplot(2,1,2)
plot(x,y,'*',x,polyval(p,x))
title('5次多项式拟合')
grid on