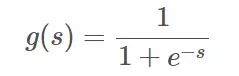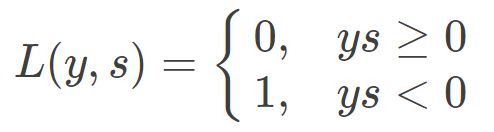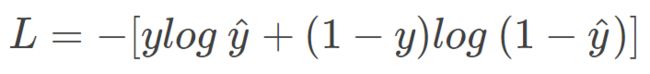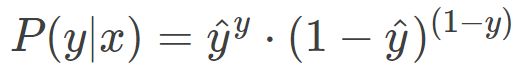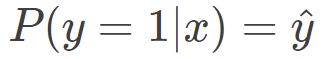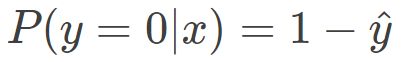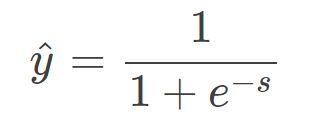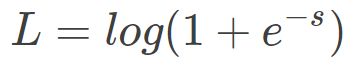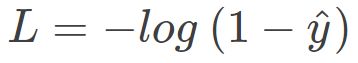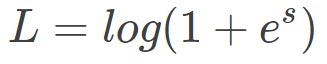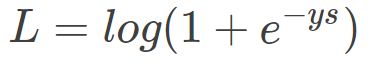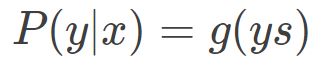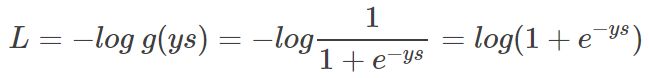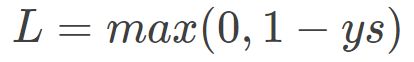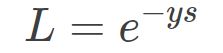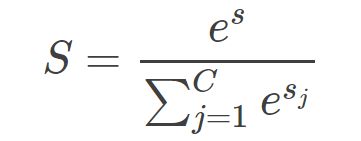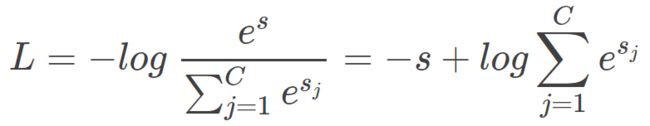确定不收藏?机器学习必备的分类损失函数速查手册
关键时刻,第一时间送达!
阅读本文需要 10 分钟
在监督式机器学习中,无论是回归问题还是分类问题,都少不了使用损失函数(Loss Function)。损失函数(Loss Function)是用来估量模型的预测值 f(x) 与真实值 y 的不一致程度。若损失函数很小,表明机器学习模型与数据真实分布很接近,则模型性能良好;若损失函数很大,表明机器学习模型与数据真实分布差别较大,则模型性能不佳。我们训练模型的主要任务就是使用优化方法来寻找损失函数最小化对应的模型参数。
在上一篇文章中,红色石头已经给大家详细介绍了回归问题常用的三个损失函数,并使用 Python 代码,感性上比较了它们之间的区别。传送门:
机器学习大牛是如何选择回归损失函数的?
今天,我们继续来了解一下分类问题中常用的损失函数,不妨一看!
0
模型输出
在讨论分类问题的损失函数之前,我想先说一下模型的输出 g(s)。一般来说,二分类机器学习模型包含两个部分:线性输出 s 和非线性输出 g(s)。其中,线性输出一般是模型输入 x 与 参数 w 的乘积,简写成:s = wx;非线性输出一般是 Sigmoid 函数,其表达式如下:
经过 Sigmoid 函数,g(s) 值被限定在 [0,1] 之间,若 s ≥ 0,g(s) ≥ 0.5,则预测为正类;若 s < 0,g(s) < 0.5,则预测为负类。
关于正类和负类的表示,通常有两种方式:一种是用 {+1, -1} 表示正负类;另一种是用 {1, 0} 表示正负类。下文默认使用 {+1, -1},因为这种表示方法有种好处。如果使用 {+1, -1} 表示正负类,我们来看预测类别与真实类别的四种情况:
s ≥ 0, y = +1: 预测正确
s ≥ 0, y = -1: 预测错误
s < 0, y = +1: 预测错误
s < 0, y = -1: 预测正确
发现了吗?显然,上面四个式子可以整合成直接看 ys 的符号即可:
若 ys ≥ 0,则预测正确
若 ys < 0,则预测错误
这里的 ys 类似与回归模型中的残差 s - y。因此,在比较分类问题的各个损失函数的时候,我们就可以把 ys 当作自变量 x 轴即可,这样更加方便。
1
0-1 Loss
0-1 Loss 是最简单也是最容易直观理解的一种损失函数。对于二分类问题,如果预测类别 y_hat 与真实类别 y 不同,则 L=1;如果预测类别 y_hat 与 真实类别 y 相同,则 L=0(L 表示损失函数)。0-1 Loss 的表达式为:
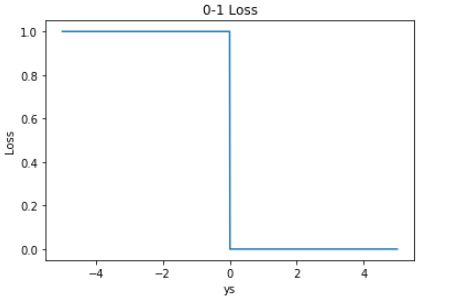
0-1 Loss 的曲线如下图所示:
0-1 Loss 的特点就是非常直观容易理解。但是它存在两个缺点:
0-1 Loss 对每个错分类点都施以相同的惩罚(损失为 1),这样对犯错比较大的点(ys 远小于 0)无法进行较大的惩罚,所有犯错点都同等看待,这不符合常理,不太合适。
0-1 Loss 不连续、非凸、不可导,难以使用梯度优化算法。
因此,实际应用中,0-1 Loss 很少使用。
2
Cross Entropy Loss
Cross Entropy Loss 是非常重要的损失函数,也是应用最多的损失函数之一。二分类问题的交叉熵 Loss 主要有两种形式,下面分别详细介绍。
第一种形式是基于输出标签 label 的表示方式为 {0,1},也最为常见。它的 Loss 表达式为:
这个公式是如何推导的呢?很简单,从极大似然性的角度出发,预测类别的概率可以写成:
我们可以这么来看,当真实样本标签 y = 1 时,上面式子第二项就为 1,概率等式转化为:
当真实样本标签 y = 0 时,上面式子第一项就为 1,概率等式转化为:
我们希望的是概率 P(y|x) 越大越好。首先,我们对 P(y|x) 引入 log 函数,因为 log 运算并不会影响函数本身的单调性。则有:
我们希望 log P(y|x) 越大越好,反过来,只要 log P(y|x) 的负值 -log P(y|x) 越小就行了。那我们就可以引入损失函数,且令 Loss = -log P(y|x) 即可。则得到损失函数为:
我们来看,当 y = 1 时:
因为,
所以,代入到 L 中,得:
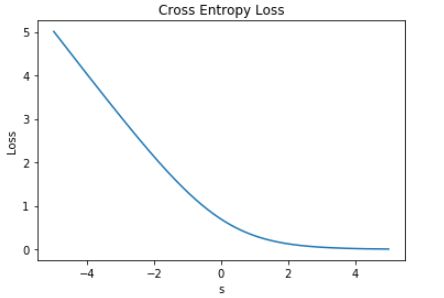
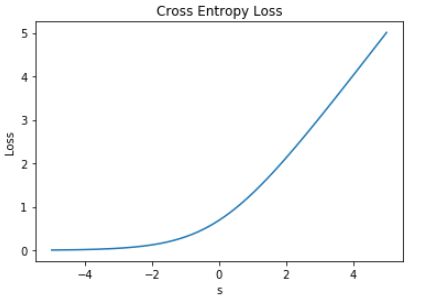
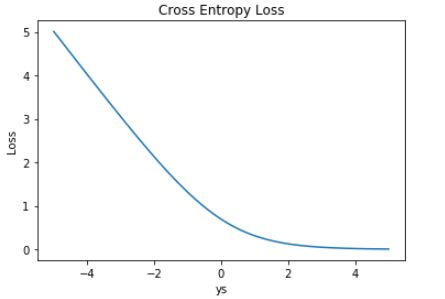
这时候,Loss 的曲线如下图所示:
从图中明显能够看出,s 越大于零,L 越小,函数的变化趋势也完全符合实际需要的情况。
当 y = 0 时:
对上式进行整理,同样能得到:
这时候,Loss 的曲线如下图所示:
从图中明显能够看出,s 越小于零,L 越小,函数的变化趋势也完全符合实际需要的情况。
第二种形式是基于输出标签 label 的表示方式为 {-1,+1},也比较常见。它的 Loss 表达式为:
下面对上式做个简单的推导,我们在 0 小节说过,ys 的符号反映了预测的准确性。除此之外,ys 的数值大小也反映了预测的置信程度。所以,从概率角度来看,预测类别的概率可以写成:
分别令 y = +1 和 y = -1 就能很容易理解上面的式子。
接下来,同样引入 log 函数,要让概率最大,反过来,只要其负数最小即可。那么就可以定义相应的损失函数为:
这时候,我们以 ys 为横坐标,可以绘制 Loss 的曲线如下图所示:
其实上面介绍的两种形式的交叉熵 Loss 是一样的,只不过由于标签 label 的表示方式不同,公式稍有变化。标签用 {-1,+1} 表示的好处是可以把 ys 整合在一起,作为横坐标,容易作图且具有实际的物理意义。
总结一下,交叉熵 Loss 的优点是在整个实数域内,Loss 近似线性变化。尤其是当 ys << 0 的时候,Loss 更近似线性。这样,模型受异常点的干扰就较小。 而且,交叉熵 Loss 连续可导,便于求导计算,是使用最广泛的损失函数之一。
3
Hinge Loss
Hinge Loss,又称合页损失,其表达式如下:
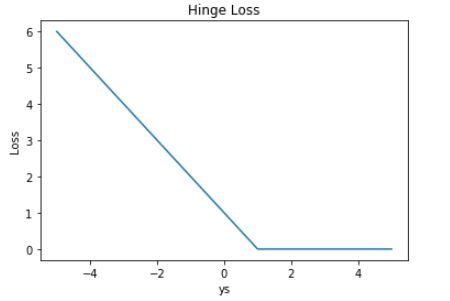
Hinge Loss 的曲线如下图所示:
Hinge Loss 的形状就像一本要合上的书,故称为合页损失。显然,只有当 ys < 1 时,Loss 才大于零;对于 ys > 1 的情况,Loss 始终为零。
Hinge Loss 一般多用于支持向量机(SVM)中,体现了 SVM 距离最大化的思想。而且,当 Loss 大于零时,是线性函数,便于梯度下降算法求导。
Hinge Loss 的另一个优点是使得 ys > 0 的样本损失皆为 0,由此带来了稀疏解,使得 SVM 仅通过少量的支持向量就能确定最终超平面。
4
Exponential Loss
Exponential Loss,又称指数损失,其表达式如下:
可以对上式进行一个直观的理解,类似于上文提到的第二种形式的交叉熵 Loss,去掉 log 和 log 中的常数 1,并不影响 Loss 的单调性。因此,推导得出了 Exponential Loss 的表达式。
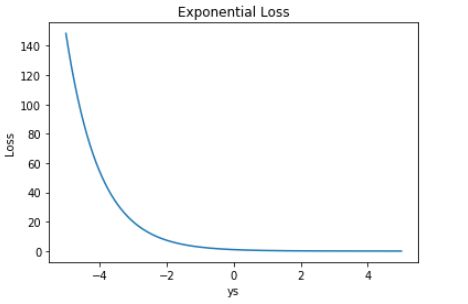
Exponential Loss 的曲线如下图所示:
Exponential Loss 与交叉熵 Loss 类似,但它是指数下降的,因此梯度较其它 Loss 来说,更大一些。
Exponential Loss 一般多用于AdaBoost 中。因为使用 Exponential Loss 能比较方便地利用加法模型推导出 AdaBoost算法。
5
Modified Huber Loss
在之前介绍回归损失函数的一篇文章里,我们介绍过 Huber Loss,它集合了 MSE 和 MAE 的优点。Huber Loss 也能应用于分类问题中,称为 Modified Huber Loss,其表达是如下:
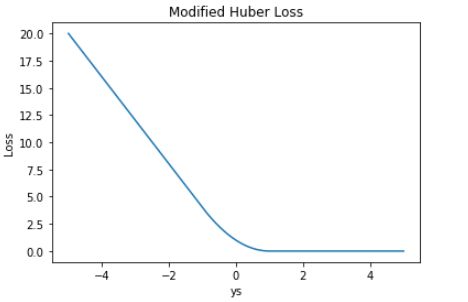
Modified Huber Loss 的曲线如下图所示:
从表达式和 Loss 图形上看,Modified Huber Loss 结合了 Hinge Loss 和 交叉熵 Loss 的优点。一方面能在 ys > 1 时产生稀疏解提高训练效率;另一方面对于 ys < −1 样本的惩罚以线性增加,这意味着受异常点的干扰较少。scikit-learn 中的 SGDClassifier 就使用了 Modified Huber Loss。
6
Softmax Loss
对于多分类问题,也可以使用 Softmax Loss。
机器学习模型的 Softmax 层,正确类别对于的输出是:
其中,C 为类别个数,小写字母 s 是正确类别对应的 Softmax 输入,大写字母 S 是正确类别对应的 Softmax 输出。
由于 log 运算符不会影响函数的单调性,我们对 S 进行 log 操作。另外,我们希望 log(S) 越大越好,即正确类别对应的相对概率越大越好,那么就可以对 log(S) 前面加个负号,来表示损失函数:
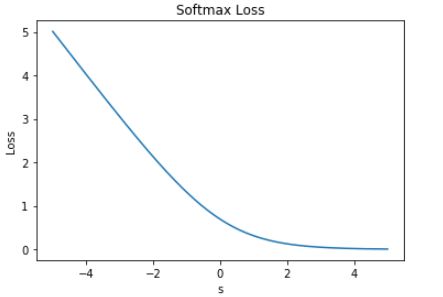
Softmax Loss 的曲线如下图所示:
上图中,当 s << 0 时,Softmax 近似线性;当 s>>0 时,Softmax 趋向于零。Softmax 同样受异常点的干扰较小,多用于神经网络多分类问题中。
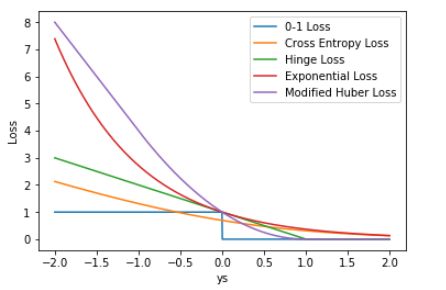
最后,我们将 0-1 Loss、Cross Entropy Loss、Hinge Loss、Exponential Loss、Modified Huber Loss 画在一张图中:
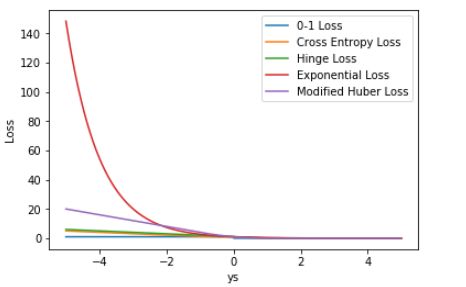
上图 ys 的取值范围是 [-2,+2],若我们把 ys 的坐标范围取得更大一些,上面 5 种 Loss 的差别会更大一些,见下图:
显然,这时候 Exponential Loss 会远远大于其它 Loss。从训练的角度来看,模型会更加偏向于惩罚较大的点,赋予其更大的权重。如果样本中存在离群点,Exponential Loss 会给离群点赋予更高的权重,但却可能是以牺牲其他正常数据点的预测效果为代价,可能会降低模型的整体性能,使得模型不够健壮(robust)。
相比 Exponential Loss,其它四个 Loss,包括 Softmax Loss,都对离群点有较好的“容忍性”,受异常点的干扰较小,模型较为健壮。
好了,以上就是红色石头总结的几个常用的分类问题的损失函数,知道这些细节和原理,对我们是很有帮助的。希望本文对你有所帮助~
推荐阅读
机器学习大牛是如何选择回归损失函数的?
我的深度学习入门路线
【干货】我的机器学习入门路线图
![]()