洛谷P3398 仓鼠找sugar - lca - 树剖

两人走路方向不同，可能一个由底到顶 一个由顶到底，但因为找的是公共点而不是相遇点，所以没有影响
先想想这个题的过程，过程有什么坑点，把坑点及时记录在注释上 这样打代码的时候不会忘
注意是棵树，是棵树 找不同情况/反例时切记贴合题意
树是种优美的结构，一个点只有一个父节点 你不能从把一个另点插到这个点上方
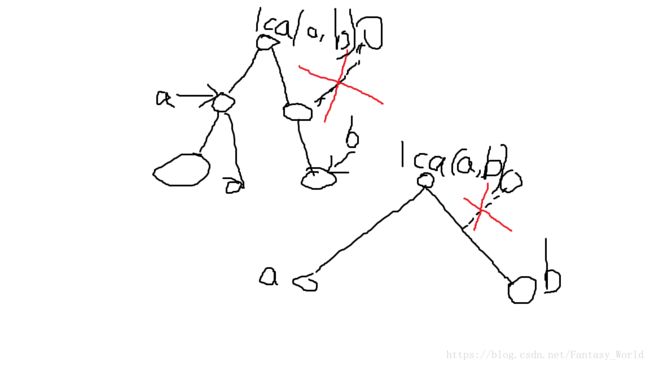
总之 不能有如下情况

应该由特殊例子找到普遍规律，再把普遍规律应用于一般例子来检验
我一开始想：cd的lca为e 那么e和a或b的lca为lca(a,b)可以吗？ 不行
一棵树非常大的时候，a b这段路处于树的中央 在检验普遍规律时，不能只画出a -> lca - >b
应该把这棵子树上下的节点都画画

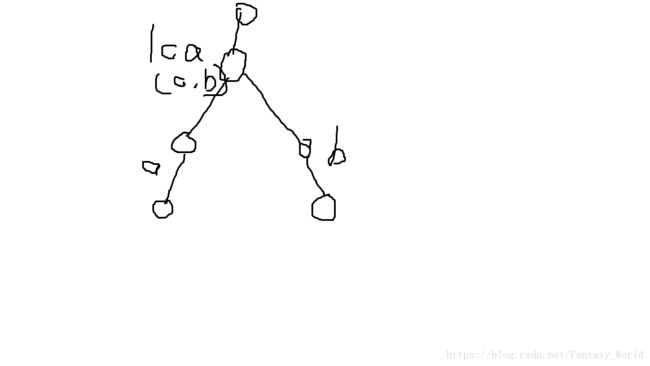
发现当cd位于a下方时不对
然后为了不陷入思维怪圈，要明确一点，ab和cd路径 没有先后之分，我们考虑的是ab和cd路径的关系 可以先固定ab路径，看什么样的cd路径能和ab路径有公共点，但这样可能在某些情况中考虑不到ab路径应该满足什么性质，而陷入死板地求解，没能灵活地看待问题，因为abcd无先后之分，所以还要固定cd找ab 就是让一条边尽量往另一条边上“靠”
所以要经常地“跳出来”重新换角度理解问题，就能走出思维怪圈，找到解法。

需要找到一个普遍的规律，那么普遍意义就说明不论是ab满足cd还是cd满足ab都要服从这个普遍规律
发现当cd的lca位于ab路径上时，路径一定相交，那么既然abcd无先后之分 同样当ab的lca位于cd路径上时 也会相交
（把自己画的图中的cd和ab位置互换即可）

现在问题转化为如何判断一个点是否在一条路径上，可以暴力爬树，但是有点难写。。。还不如一开始就打差分得暴力分
但是可以发现一个点p在s,t路径上（设lca(s,t)为q）那么p一定比q更深，p是q的子节点，并且p要么属于a-lca 要么属于lca-b 这样的话分两种可能，若p在a-lca，考虑到这是一棵树，一个点向上走只能走出来一条链，并且都是他的祖先，那么实际上就是a向上走的过程中“碰到了p”，换句话说p是a的祖先，既然谈到祖先了，不妨用一下lca，毕竟lca就是在求祖先，那么有lca(a, p) = p

灵活运用一下lca有哪些性质就可以了

也可以树剖做。。。对一段路径进行标记（标记为++tot），查询另一段路径上是否有标记，为了避免每次清空，可以比较两端路径被标记上的最大值，若相等则有公共点

#include 
#include 
#include 
#include 
using namespace std;
#define debug(x) cerr << #x << "=" << x << endl;
const int MAXN = 100000 + 10;
int f[MAXN][22],n,pat[3][MAXN],tepa[MAXN],vis[MAXN],g[MAXN][22],ans;
int q,fa[MAXN],last[MAXN],depth[MAXN],tot,tot1,tot2,tetot,dif[MAXN];
struct query{
    int a,b,c,d;
}qu[MAXN];
struct Edge{
    int u,v,to;
    Edge(){}
    Edge(int u, int v, int to) : u(u), v(v), to(to) {}
}e[MAXN * 2];
inline void add(int u, int v) {
    e[++tot] = Edge(u,v,last[u]);
    last[u] = tot;
}
void lca_dfs(int x) {
    for(int i=last[x]; i; i=e[i].to) {
        int v = e[i].v;
        if(depth[v]) continue;
        depth[v] = depth[x] + 1;
        f[v][0] = x;
        lca_dfs(v);
    }
}
void lca_init() {
    depth[1] = 1;
    lca_dfs(1);
    for(int k=1; k<=20; k++) {
        for(int i=1; i<=n; i++) {
            f[i][k] = f[f[i][k-1]][k-1];
        }
    }
}
int lca(int x, int y) {
    if(depth[x] < depth[y]) swap(x, y); //x??y
    for(int k=20; k>=0; k--) {
        if(depth[f[x][k]] >= depth[y]) x = f[x][k];
    } 
    if(x == y) return x;
    for(int k=20; k>=0; k--) {
        if(f[x][k] != f[y][k]) x = f[x][k], y = f[y][k];
    }
    return f[x][0];
}
void dfs(int x) {
    vis[x] = 1;
    for(int i=last[x]; i; i=e[i].to) {
        int v = e[i].v;
        if(vis[v]) continue;
        vis[v] = 1;
        dfs(v);
        fa[x] += fa[v];
    }
}
void solve1() {//树上差分暴力分
    for(int i=1; i<=q; i++) {
        int a = qu[i].a, b = qu[i].b, c = qu[i].c, d = qu[i].d;
        int lcca = lca(a,b);//写lcc1不如写lcca
        int lccc = lca(c,d);
        memset(vis, 0, sizeof(vis));
        memset(fa, 0 ,sizeof(fa));//多组询问清空该清空的数组
        fa[a]++, fa[b]++, fa[f[lcca][0]]-=1,fa[lcca]-=1;
        fa[c]++, fa[d]++, fa[f[lccc][0]]-=1,fa[lccc]-=1;//让该为0的为0
        dfs(1);
        bool flg = false;//注意每次重置
        for(int i=1; i<=n; i++) {
            if(fa[i] >= 2) flg = true;
        }
        if(flg) printf("Y\n");
        else printf("N\n");
    }
}
void solve2() {
    for(int i=1; i<=q; i++) {
        int a = qu[i].a, b = qu[i].b, c = qu[i].c, d = qu[i].d;
        int lab = lca(a, b);
        int lcd = lca(c, d);
        if(depth[lcd] >= depth[lab]) {
            if(lca(a, lcd) == lcd || lca(b, lcd) == lcd) {
                printf("Y\n");
                continue;
            }
        } else {
            if(lca(c, lab) == lab || lca(d, lab) == lab) {
                printf("Y\n");
                continue;
            }
        }
        printf("N\n");
    }
}
int main() {
    scanf("%d %d", &n, &q);
    for(int i=1; iint u,v;
        scanf("%d %d", &u, &v);
        add(u,v);
        add(v,u);
    }
    lca_init(); 
    for(int i=1; i<=q; i++) {
        int a,b,c,d;
        scanf("%d %d %d %d", &qu[i].a, &qu[i].b, &qu[i].c, &qu[i].d);
    }
    solve2();
    return 0;
}