对斜率优化的一点理解(围绕图讲解)
P3195 [HNOI2008]玩具装箱
这道题作为斜率优化入门真是再好不过了,我也不例外
普 通 的 转 移 方 程 普通的转移方程 普通的转移方程
d p [ i ] = d p [ j ] + ( s u m [ i ] − s u m [ j ] + i − j − 1 − l ) 2 dp[i]=dp[j]+(sum[i]-sum[j]+i-j-1-l)^2 dp[i]=dp[j]+(sum[i]−sum[j]+i−j−1−l)2
这 是 n 2 的 算 法 , 考 虑 如 何 O ( 1 ) 找 到 前 面 最 优 的 j 转 移 这是n^2的算法,考虑如何O(1)找到前面最优的j转移 这是n2的算法,考虑如何O(1)找到前面最优的j转移
Ⅰ . 化 简 d p 方 程 \color{Red}Ⅰ.化简dp方程 Ⅰ.化简dp方程
令 A = s u m n [ i ] + i , 因 为 现 在 是 在 转 移 i , 所 以 A 是 个 定 值 令A=sumn[i]+i,因为现在是在转移i,所以A是个定值 令A=sumn[i]+i,因为现在是在转移i,所以A是个定值
令 B = s u m n [ j ] + j + l + 1 , 因 为 j 不 固 定 , 所 以 B 是 个 变 化 的 量 令B=sumn[j]+j+l+1,因为j不固定,所以B是个变化的量 令B=sumn[j]+j+l+1,因为j不固定,所以B是个变化的量
那 么 代 入 得 那么代入得 那么代入得
d p [ i ] = d p [ j ] + ( A − B ) 2 dp[i]=dp[j]+(A-B)^2 dp[i]=dp[j]+(A−B)2
化简得到
d p [ i ] = d p [ j ] + A 2 + B 2 − 2 A B dp[i]=dp[j]+A^2+B^2-2AB dp[i]=dp[j]+A2+B2−2AB
移项得到
d p [ j ] + B 2 = 2 A B + d p [ i ] − A 2 dp[j]+B^2=2AB+dp[i]-A^2 dp[j]+B2=2AB+dp[i]−A2
如 果 把 y 看 成 d p [ j ] + B 2 , 把 x 看 成 B 如果把y看成dp[j]+B^2,把x看成B 如果把y看成dp[j]+B2,把x看成B
那 么 这 条 直 线 得 斜 率 已 经 确 定 , 是 2 A , 是 定 值 那么这条直线得斜率已经确定,是2A,是定值 那么这条直线得斜率已经确定,是2A,是定值
现 在 的 目 标 是 去 前 面 找 一 个 j 点 , 来 确 定 x 和 y 让 截 距 最 小 现在的目标是去前面找一个j点,来确定x和y让截距最小 现在的目标是去前面找一个j点,来确定x和y让截距最小
为 啥 ? 截 距 是 d p [ i ] − A 2 , A 是 定 值 , 截 距 最 小 就 是 d p [ i ] 最 小 为啥?截距是dp[i]-A^2,A是定值,截距最小就是dp[i]最小 为啥?截距是dp[i]−A2,A是定值,截距最小就是dp[i]最小
Ⅱ . 怎 么 找 前 面 最 优 的 j \color{Red}Ⅱ.怎么找前面最优的j Ⅱ.怎么找前面最优的j
我 们 知 道 前 面 每 个 j 对 应 一 个 点 ( B j , d p [ j ] + B j 2 ) 我们知道前面每个j对应一个点(B_j,dp[j]+B_j^2) 我们知道前面每个j对应一个点(Bj,dp[j]+Bj2)
所 以 只 有 下 凸 包 上 的 点 才 有 可 能 作 为 最 优 的 j 来 转 移 , 至 于 为 什 么 所以只有下凸包上的点才有可能作为最优的j来转移,至于为什么 所以只有下凸包上的点才有可能作为最优的j来转移,至于为什么
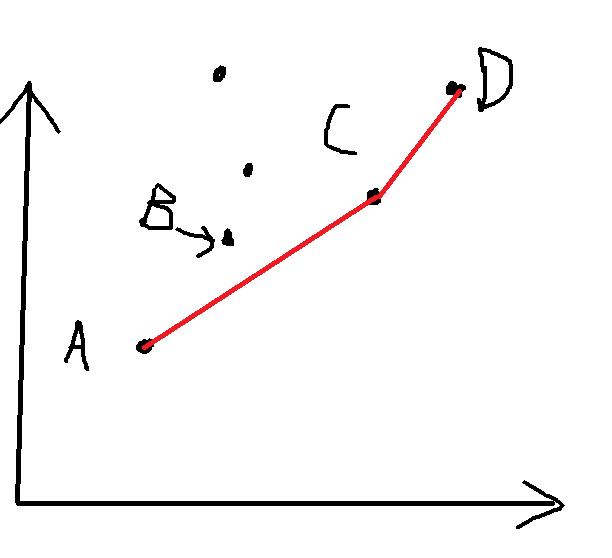
比 如 这 么 多 点 , 只 需 要 维 护 下 凸 包 A C D 即 可 , 为 什 么 不 需 要 B ? 比如这么多点,只需要维护下凸包ACD即可,为什么不需要B? 比如这么多点,只需要维护下凸包ACD即可,为什么不需要B?
当 2 A 大 于 C A 的 斜 率 时 , 选 C 点 的 截 距 明 显 小 于 选 B 的 截 距 当2A大于CA的斜率时,选C点的截距明显小于选B的截距 当2A大于CA的斜率时,选C点的截距明显小于选B的截距
当 2 A 小 于 C A 的 斜 率 时 , 选 A 点 的 截 距 明 显 小 于 选 B 的 截 距 当2A小于CA的斜率时,选A点的截距明显小于选B的截距 当2A小于CA的斜率时,选A点的截距明显小于选B的截距
所 以 不 在 下 凸 包 的 点 完 全 无 用 , 直 接 丢 掉 就 好 了 ( 怎 么 丢 , 下 面 讲 ) 所以不在下凸包的点完全无用,直接丢掉就好了(怎么丢,下面讲) 所以不在下凸包的点完全无用,直接丢掉就好了(怎么丢,下面讲)
那 下 凸 包 上 哪 个 j 最 优 ? 那下凸包上哪个j最优? 那下凸包上哪个j最优?
显 然 , 当 下 凸 包 相 邻 两 点 的 斜 率 小 于 2 A 时 , 越 右 边 的 j 形 成 的 截 距 越 小 显然,当下凸包相邻两点的斜率小于2A时,越右边的j形成的截距越小 显然,当下凸包相邻两点的斜率小于2A时,越右边的j形成的截距越小
但 是 当 斜 率 大 于 2 A 时 , 形 成 的 截 距 反 而 大 ( 红 线 是 斜 率 2 A ) 但是当斜率大于2A时,形成的截距反而大(红线是斜率2A) 但是当斜率大于2A时,形成的截距反而大(红线是斜率2A)

如 上 图 , B C 是 刚 好 大 于 2 A 的 直 线 , 所 以 B 点 截 距 最 小 , 最 优 如上图,BC是刚好大于2A的直线,所以B点截距最小,最优 如上图,BC是刚好大于2A的直线,所以B点截距最小,最优
所以具体做法是开个单调队列维护下凸包上的点
一直弹出队首元素直到斜率大于2A,那就是最优的j
但 是 同 时 我 们 要 维 护 单 调 队 列 中 只 存 在 下 凸 包 上 的 点 , 这 该 怎 么 办 ? 但是同时我们要维护单调队列中只存在下凸包上的点,这该怎么办? 但是同时我们要维护单调队列中只存在下凸包上的点,这该怎么办?
怎 样 把 不 在 下 凸 包 上 的 点 排 除 ? 怎样把不在下凸包上的点排除? 怎样把不在下凸包上的点排除?
就 是 根 据 斜 率 来 判 断 , 下 凸 包 就 是 相 邻 两 点 的 斜 率 递 增 就是根据斜率来判断,下凸包就是相邻两点的斜率递增 就是根据斜率来判断,下凸包就是相邻两点的斜率递增
那 么 就 在 单 调 队 列 找 最 近 的 两 个 在 队 列 的 点 ( 也 就 是 从 队 尾 找 ) 那么就在单调队列找最近的两个在队列的点(也就是从队尾找) 那么就在单调队列找最近的两个在队列的点(也就是从队尾找)
如 果 斜 率 不 满 足 递 增 , 就 一 直 弹 出 如果斜率不满足递增,就一直弹出 如果斜率不满足递增,就一直弹出
然 后 把 当 前 的 i 放 入 队 尾 即 可 然后把当前的i放入队尾即可 然后把当前的i放入队尾即可
附 上 代 码 附上代码 附上代码
#include
using namespace std;
const int maxn=5e5+10;
int n,l;
int head,tail,q[maxn];
double sumn[maxn],dp[maxn];
double a(int i){
return i+sumn[i];
}
double b(int i){
return sumn[i]+i+l+1;
}
double x(int i){
return b(i);
}
double y(int i){
return dp[i]+b(i)*b(i);
}
double xie(int i,int j){
return (y(i)-y(j) )/( x(i)-x(j) );
}
int main()
{
cin >> n >> l;
for(int i=1;i<=n;i++)
{
cin >> sumn[i];
sumn[i]+=sumn[i-1];
}
head=tail=1;
for(int i=1;i<=n;i++)
{
while( head