机器学习.png
Kmeans是最简单的一种分类算法，其基本思想是基于距离的思想。即一个待分类的东西，假设要归类为A类或者B类，则根据这个东西离A类和B类哪个距离更近来决定，离A近就是A类，离B近就是B类。当然你可能不止只有两类，但n类的情况也是一样的，离哪个类近就是那类。
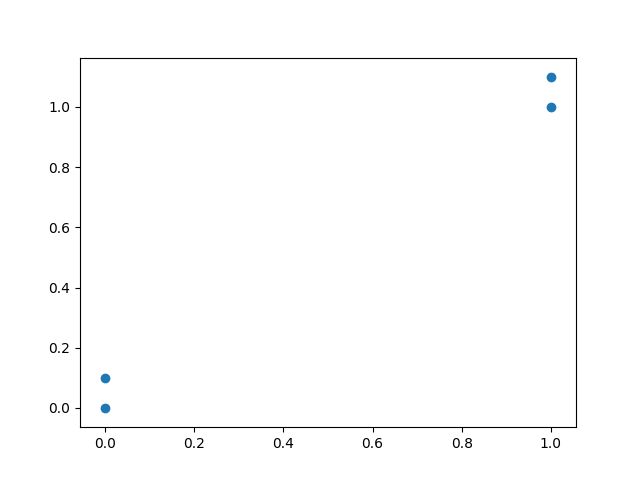
以最简单的二维坐标为例子讲一下，下面这个图，有四个点[1,1.1], [1,1], [0,0], [0,0.1]
Paste_Image.png
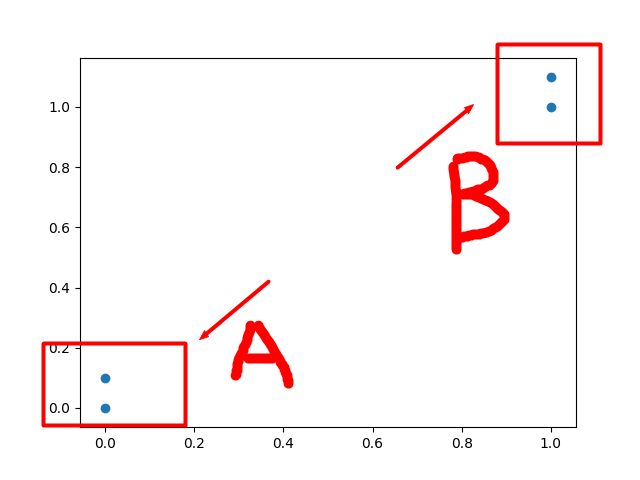
我们可以很合理的认为左下角两个点是一类，叫A类。
右上角的两个点是一类，叫B类。
分类图.png
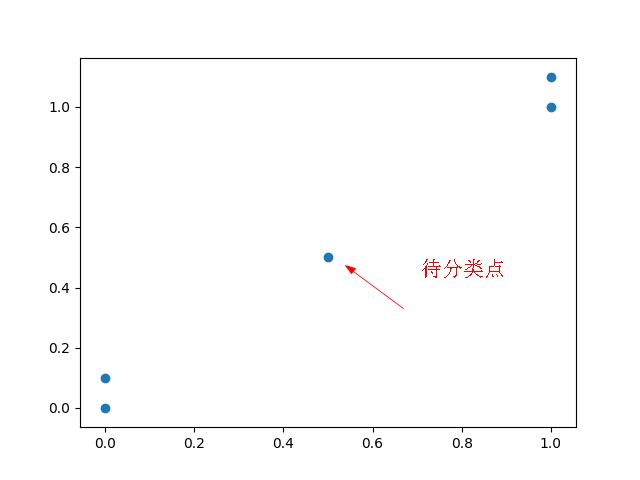
那如果我们这时来了一个点[0.5,0.5]，如何给这个点分类呢，是A类还是B类呢？有没有什么衡量的标准呢？很简单，根据距离就可以了。找出距离这个点最近的k个点，k个点中A中的点多，就属于A类，B中的点多，就属于B类。
待分类点.png
距离计算，直接是用矩阵减法，然后再平方就行。像下面这样。
矩阵计算.png
如果kmean算法选择k=3，这最近的三点距离是0.4，0.5，0.5。对应的分类是B，B，A。B的数量大于A。说明待分类的点属于B类。分类完成。
下面是Python的实现。部分摘自《机器学习实战》，为了更好看，我把他整成一个文件了。
from numpy import *
import operator
def createDataSet():
group = array([[1.0,1.1],[1.0,1.0],[0,0],[0,0.1]])
labels = ['A','A','B','B']
return group, labels
def classify0(inX, dataSet, labels, k):
dataSetSize = dataSet.shape[0]
diffMat = tile(inX, (dataSetSize,1)) - dataSet ##矩阵相减
sqDiffMat = diffMat**2 ##差值平方
sqDistances = sqDiffMat.sum(axis=1)
sortedDistIndicies = sqDistances.argsort() ##对距离进行排序
classCount={} ##新建字典，字典常用于排序
for i in range(k): ##对字典进行排序，字典以labal作为key，数值为kmean的数值
voteIlabel = labels[sortedDistIndicies[i]]
classCount[voteIlabel] = classCount.get(voteIlabel,0) + 1
sortedClassCount = sorted(classCount.iteritems(), key=operator.itemgetter(1), reverse=True)
print("dictionary",sortedClassCount)
return sortedClassCount[0][0]
group,labels=createDataSet()
result=classify0([0.5,0.5], group, labels, 3)
print(result) ##显示结果
上面的程序大家可以打一下log，跟踪一下矩阵的变化。
最后打印结果是,分类为B，字典中B有两个，A有一个。说明要分类为B。
('dictionary', [('B', 2), ('A', 1)])
B