【全部译文】Deep-Waveform: A Learned OFDM Receiver Based on Deep Complex Convolutional Networks

翻译I-III部分参考以下博客，剩余部分由本人借助百度翻译完成，有翻译错误的地方请评论指出，谢谢。
https://blog.csdn.net/snowsnowsnow1991/article/details/106787644#commentBox
论文PDF下载
论文中原图下载–点击sources

Abstract

Recent explorations of Deep Learning in the physical layer (PHY) of wireless communication have shown the capabilities of Deep Neuron Networks in tasks like channel coding, modulation, and parametric estimation. However, it is unclear if Deep Neuron Networks could also learn the advanced waveforms of current and next-generation wireless networks, and potentially create new ones. In this paper, a Deep Complex Convolutional Network (DCCN) without explicit Discrete Fourier Transform (DFT) is developed as an Orthogonal FrequencyDivision Multiplexing (OFDM) receiver. Compared to existing deep neuron network receivers composed of fully-connected layers followed by non-linear activations, the developed DCCN not only contains convolutional layers but is also almost (and could be fully) linear. Moreover, the developed DCCN not only
learns to convert OFDM waveform with Quadrature Amplitude Modulation (QAM) into bits under noisy and Rayleigh channels, but also outperforms expert OFDM receiver based on Linear Minimum Mean Square Error channel estimator with prior channel knowledge in the low to middle Signal-to-Noise Ratios of Rayleigh channels. It shows that linear Deep Neuron Networks could learn transformations in signal processing, thus master advanced waveforms and wireless channels. Index Terms Wireless Communications, Physical Layer, Deep Learning, Artificial Neuron Networks, OFDM, Modulation.

近年来对无线通信物理层深度学习的研究表明，深度神经元网络在信道编码、调制和参数估计等方面具有良好的性能。然而，目前还不清楚深层神经元网络是否也能学习当前和下一代无线网络的先进波形，并有可能创造出新的波形。在本文中，开发了一种没有明确的离散傅里叶变换（DFT）的深度复数卷积网络（DCCN）作为正交频分复用（OFDM）接收器。与现有的由全连接层和非线性激活组成的深度神经元网络接收器相比，所开发的DCCN不仅包含卷积层，而且几乎是（可能是完全）线性的。此外，所开发的DCCN不仅能够学习在噪声和瑞利信道下将正交幅度调制（QAM）的OFDM波形转换为比特，而且在瑞利信道的中、低信噪比下，其性能也优于基于线性最小均方误差信道估计器的专业OFDM接收机。结果表明，线性深度神经元网络能够学习信号处理中的变换，从而掌握高级波形和无线信道。

I. INTRODUCTION

Despite the great success of Deep Learning in a number of fields, its application in wireless communication, especially the physical layer (PHY), was explored only very recently [1]–[9]. Many considered that phenomenons in the physical layer of over-the-air wireless communication, such as noise, fading, channel impairment, etc, have been understood, and addressed by well-established theories of signal and coding. On the other hand, although some progresses, such as signal classification, have been achieved in recent works [1]–[9], it is yet unclear if Deep Learning (DL), known as a black box approach good at structured tasks those are easy for human while hard for traditional analytical approaches, would be able to outperform white-box approaches, such as signal and coding theories.

尽管深度学习在许多领域取得了巨大的成功，但其在无线通信中的应用，尤其是物理层（PHY）的应用是最近才被探索出来的[1]-[9]。许多人认为，空中无线通信物理层的现象，如噪声、衰落、信道损伤等，已经被理解，并由成熟的信号和编码理论解决。另一方面，虽然在最近的工作中取得了一些进展，如信号分类[1]-[9]，但深度学习(Deep Learning，DL)作为一种黑盒方法，擅长于人类容易而传统分析方法难以完成的结构化任务，是否能够胜过信号和编码理论等白盒方法，目前还不清楚。

Currently, the applications of DL in wireless communications are mostly focused on enhancing certain functionalities [7], [10]. Above the PHY level, DL is applied in resource management, such as traffic prediction on network level [11], interference alignment [12], as well as decision makings such as power control and spectrum sharing [13]. Among the researches of DL in PHY, many works focus on enhancing certain components in wireless system [7], such as signal classification [1], [2], detection [8], channel coding [3], [5], channel estimation [8], [14], [15], Direction-of-Arrival (DoA) estimation [14], or control problems such as antenna titling. Another thread of researches attempt to establish a novel, end-to-end, communication architecture entirely based on Deep Neuron Networks (DNN) [4], [6], [7].

目前，DL在无线通信中的应用多集中在增强某些功能上[7]、[10]。在PHY层以上，DL应用于资源管理，如网络层的流量预测[11]、干扰配准[12]，以及功率控制和频谱共享等决策[13]。在物理场域DL的研究中，许多工作集中在增强无线系统的某些组件[7]，如信号分类[1]、[2]、检测[8]、信道编码[3]、[5]、信道估计[8]、[14]、[15]、到达方向(DoA)估计[14]或控制问题如天线滴定。另一条研究线索是试图建立一个完全基于深度神经元网络（DNN）的新型端到端通信架构[4]，[6]，[7]。

Among these efforts, building a DL-based end-to-end wireless communication architecture is the most aggressive attempt that could potentially transform the field that is largely based on expert knowledge and models. In [4], [6], the end-to-end wireless PHY is viewed as an autoencoder (AE), as illustrated in Fig. 1. Compared to a typical AE in the DL field that processes structured data such as image and natural language, as shown in Fig. 1, a communication AE has two unique characters: First, the objective of communication AE is to find latent coding that can carry information over detrimental wireless channel, generally by increasing the redundancy, while typical AE is intended to find compact representations of structured data in lower-dimensional latent space without concern of pollution of the code. Second, communication AE is designed to learn the inherit behaviors of channel rather than the structure of data. Data in a communication AE–input and output bits–is considered unstructured and incompressible. Therefore, an communication AE should be trained over a set of channel(s) with random data.

在这些努力中，构建基于DL的端到端无线通信架构是最积极的尝试，它有可能改变这个主要基于专家知识和模型的领域。在[4]、[6]中，端到端无线PHY被看作是一个自动编码器（AE），如图1所示。与DL领域典型的处理图像、自然语言等结构化数据的AE相比，通信AE具有两个独特的特点，如图1所示。第一，通信AE的目标是寻找能够在不利的无线信道上携带信息的隐藏编码，一般是通过增加冗余度来实现，而典型AE的目的是在低维的潜伏空间中寻找结构化数据的紧凑表示，而不担心编码的污染。其次，通信AE的目的是学习信道的继承行为，而不是数据的结构。通信AE中的数据–输入和输出位–被认为是非结构化和不可压缩的。因此，通信AE应该在一组随机数据的通道上进行训练。

Numerical and experimental evaluations in [4], [6] demonstrate the capability of DNN in learning key PHY functionalities all together, e.g. channel coding, modulation, carrier synchronization. QAM-like constellations different from those designed by experts are created by their AEs. However, none of these works have shown the ability of DNN in mastering advanced waveforms in modern wireless networks, such as the family of Orthogonal Frequency Division Modulation (OFDM). Furthermore, AEs in [4], [6] have not outperformed expert-designed wireless communication systems.

在[4]、[6]中的数值和实验评估证明了DNN在学习关键的PHY功能方面的能力，例如信道编码、调制、载波同步等。由其AE创建了不同于专家设计的QAM-like星图。然而，这些工作都没有显示出DNN在掌握现代无线网络中高级波形的能力，如正交频分调制系列 (OFDM)。此外，[4]、[6]中的AE也没有优于专家设计的无线通信系统。

Building an DNN that work with OFDM signal without using explicit Discrete Fourier Transform (DFT) module is a clear demonstration of the capability of DL in learning (and potentially creating) advanced waveforms. Waveform generation relies on various complex convolutions, such as filter and DFT, on digital base-band signal that is typically represented as complex number–the In-Phase and Quadrature (IQ) data. However, complex convolution is not currently supported by popular Deep Learning platforms, such as TensorFlow [16], Keras [17]. On the other hand, due to the lack of theoretical guidance on using non-linear activations, the extensive usages of Rectified Linear Unit (Relu) [4], [6], [8] seems to contradict with existing, generally linear, signal processing techniques.

在不使用明确的离散傅里叶变换(DFT)模块的情况下，建立一个能处理OFDM信号的DNN是DL在学习(和潜在的创造)高级波形方面的能力的一个明显证明。波形的生成依赖于各种复数的卷积，如滤波器和DFT，在数字基带信号上，通常以复数表示–同相和正交（IQ）数据。然而，目前流行的深度学习平台并不支持复数卷积，如TensorFlow[16]、Keras[17]。另一方面，由于缺乏使用非线性激活的理论指导，线性修正单元（Relu）[4]、[6]、[8]的大量使用似乎与现有的、一般线性的信号处理技术相矛盾。

In this paper, an OFDM receiver entirely based on Deep Complex Convolutional Network (DCCN) is developed without using any FFT/IFFT modules. The DCCN receiver contains a basic OFDM receiver and a separated channel equalizer. Following the principle of signal processing, the developed DCCN model is significantly different from existing works [4], [6], [8] that only use Fully-Connected hidden layers with Rectified Linear Unit (Relu) activation. Our model contains both dense and convolutional layers which are mostly linearactivated, and new structures of residual and skip connections. Moreover, complex convolutional layer is implemented within Tensorflow [16] to process complex IQ data, instead of treating it as two independent real numbers. The DCCN-based OFDM receiver achieves similar bit error rate (BER) of an expert receiver on 2,4,8, and 16 QAMs in AWGN channel, and learns to exploit the Cyclic Prefix to outperform an LMMSE channel estimator with prior channel information in Rayleigh channels over low to middle SNRs. This work shows the capabilities of Deep Learning in complex signal transformations that are key to master waveforms and channel behaviors.

本文在不使用任何FFT/IFFT模块的情况下，开发了一种完全基于深度复数卷积网络(DCCN)的OFDM接收机。DCCN接收器包含一个基本的OFDM接收器和一个分离的信道均衡器。遵循信号处理的原理，所开发的DCCN模型与现有的作品[4]、[6]、[8]仅使用线性修正单元(Relu)激活的全连接隐藏层有很大不同。我们的模型包含了稠密层和卷积层，而卷积层大多是线性激活的，同时还包含了residual connections 和 skip connections的新结构。此外，复数卷积层是在Tensorflow[16]内实现的，用于处理复数的IQ数据，而不是将其作为两个独立的实数处理。在AWGN信道中，基于DCCN的OFDM接收机在 2,4,8和16 QAMs上实现了与专家接收机相似的误码率(BER)，并且学会了利用循环前缀，在中低信噪比的Rayleigh信道中优于使用事先信道信息的LMMSE信道估计器。这项工作显示了深度学习在复数信号变换中的能力，而这是主波形和信道行为的关键。

The rest of this paper is organized as follows: Related work is discussed in Section II. OFDM communication system is introduced in Section III. In Section IV, the model and training approaches of DCCN receiver and equalizer are introduced. Numerical evaluation results are presented in Sections V. Finally, the paper is concluded in Section VI.

本文其余部分组织如下: 第二节讨论了相关工作。第三节介绍了OFDM通信系统。在第四节中，介绍了DCCN接收器和均衡器的模型和训练方法。数值评估结果在第五节中介绍，最后，第六节对本文做了总结。

II. RELATED WORK

A. Deep Learning in PHY of Wireless Communications

Deep learning for wireless communication in physical layeremerged only lately. In surveys [7], [10], it is pointed out that Deep learning could be used for modulation recognition, channel decoding, and detection to enhance existing wireless communication system, and can also be used to construct novel communication architecture, extend existing expert knowledge, for multi-user and MIMO. In [1], a convolutional (Conv) network is developed to classify the modulation of radio signal. In [2], a Radio Transformer Network (RTN) based on Conv and FC layers with Relu activations is developed for parametric estimation and recover signal, e.g. from Carrier Frequency Offset (CFO). Despite Complex Convolutional (CConv) layer is introduced in [2], it is not used in RTN, in which complex number is represented by power and phase but real and imaginary parts. For many tasks, this representation could be problematic as the phases of two nearby samples may jump from m π to π. An end-to-end wireless communication architecture based entirely on DNN is introduced in [4], where the entire PHY is viewed as an autoencoder trained by unsupervised learning. The Deep Learning PHY is expanded to multiple-input multiple output (MIMO) system in [5] by introducing spatial-temporal coding. The DNN models in [4], [5] are both based on dense (Fully-Connected (FC)) layers, normalization, and activations such as Relu and Softmax. Channel State Information (CSI) is estimated in [5] via FC layers with Relu activation at the receiver. In [3], Deep Learning based channel encoding is explored in AWGN channel with impairment. Comparison in [3] shows that DNN networks (Fully-Connected Layers) always outperform or equal to CNN networks (network with Convolutional (Conv) layers). In [6], an DL based end-to-end communication system is developed, where dense layers with Relu are used at both transmitter and receiver. However, the resulted BER performance in [6] underperforms existing DQPSK in both AWGN simulation and real channels. In [18], an OFDM end-to-end autoencoder based on FC layers and DFT/IDFT is claimed to outperform the QPSK with MMSE channel estimation in block error rate (BLER). However, to the best of our knowledge, learning advanced waveforms have not been addressed in all those works.

深度学习在物理层无线通信中的应用是最近才出现的，在调查[7]，[10]中指出深度学习可以用于调制识别、信道解码和检测，增强现有的无线通信系统，也可以用于构建新型的通信架构。在调查[7]、[10]中指出，深度学习可用于调制识别、信道解码和检测，以增强现有的无线通信系统，也可用于构建新颖的通信架构，扩展现有的专家知识，用于多用户和MIMO。在[1]中，开发了卷积(Conv)网络来对无线电信号的调制进行分类。在[2]中，开发了一个基于Conv和FC层的包含Relu激活的无线电变换网络(RTN)，用于参数化估计和恢复信号，例如从载波频率偏移(CFO)。尽管在[2]中引入了复数卷积层(Convolutional, CConv)，但它并没有在RTN中使用，在RTN中，复数是由功率和相位来表示的，而是由实部和虚部来表示的。对于许多任务来说，这种表示方式可能会有问题，因为附近两个样本的相位可能会从mπ跳到π。 [4]中介绍了一种完全基于DNN的端到端无线通信架构，整个PHY被看作是一个由无监督学习训练的自动编码器。在[5]中，通过引入空间-时间编码，将深度学习PHY扩展为多输入多输出（MIMO）系统。[4]、[5]中的DNN模型都是基于密集(Fully-Connected，FC)层、归一化和激活，如Relu和Softmax。在[5]中，信道状态信息(CSI)是通过FC层与接收机的Relu激活来估计的。在[3]中，探讨了基于深度学习的信道编码在AWGN信道中的损伤。在[3]中的比较表明，DNN网络(全连接层)的性能总是优于或等于CNN网络(带有卷积(Conv)层的网络)。在[6]中，开发了一种基于DL的端到端通信系统，在发射机和接收机上都使用了Relu的密集层。然而，[6]中得到的误码率性能在AWGN模拟和实际信道中都低于现有的DQPSK。在[18]中，一种基于FC层和DFT/IDFT的OFDM端到端自动编码器被认为在块误差率(BLER)方面优于带MMSE信道估计的QPSK。然而，据我们所知，所有这些工作中都没有解决学习高级波形的问题。

B. OFDM System and Its Enhancements

OFDM system is the most popular system in modern wireless communication. In [19], [20], the OFDM physical layer and various channel estimation approaches are introduced. Any improvements on OFDM system would significant impact the existing wireless system. Several enhancements is proposed to improve OFDM system, such as , Filter Bank MultiCarrier (FBMC), UFMC, GFDM [21] for next generation communication system such as 5G. These new waveforms are generally modifications of OFDM for better characteristics with regards to various interferences. An constellation enhancement approach [22] and DL-based coding system [23] are proposed to reduce the Peak to Average Power Ratio (PAPR) of OFDM waveform.

OFDM系统是现代无线通信中最流行的系统。在[19]、[20]中，介绍了OFDM物理层和各种信道估计方法。对OFDM系统的任何改进都会对现有的无线系统产生重大影响。提出了几种改进OFDM系统的方法，如 ，滤波器组多载波(FBMC)、UFMC、GFDM [21]，用于5G等下一代通信系统。这些新的波形一般都是OFDM的修改，以获得对各种干扰更好的特性。提出了一种星座增强方法[22]和基于DL的编码系统[23]，以降低OFDM波形的峰均功率比（PAPR）。

At the receiver side, several works explored the use of Cyclic Prefix (CP) to enhance the performance of OFDM receiver [24]–[27]. CP is a redundancy of time-domain OFDM symbol which is necessary to mitigate intersymbol interference (ISI), but takes up a portion of spectrum resource in time domain. A key of exploiting CP is to determine the unpolluted length in CP. Our work is a complementary of existing analytical approaches, such as Maximum Likelihood [24], [26], Factor Graph [25], [27] in exploiting CP.

在接收端，有几项工作探讨了使用循环前缀(CP)来提高OFDM接收机的性能[24]-[27]。CP是时域OFDM符号的冗余，它是缓解符号间干扰(ISI)所必需的，但会占用时域的部分频谱资源。利用CP的一个关键是确定CP中的未污染长度。我们的工作是对现有分析方法的补充，如最大似然[24]，[26]，因子图[25]，[27]为对CP的利用。

Several recent works focus on DL-based enhancements of OFDM receiver [8], [9]. In [8], an 5-layer DNN-based OFDM receiver simultaneously implements channel estimation and modulation symbol recovery. Their model uses Relu activation for hidden layers, and sigmoid for output, and equalization and recovery are trained in 2 stages. However, channel equalizer and receiver are separated in this paper, and our receiver directly output bits instead of IQ data. Moreover, [8] only studies QPSK with a block type pilot, of which could not be replicated for higher order modulation with direct bit output. A DL-based OFDM receiver in [9] is claimed outperforming LMMSE channel estimator by initialized to known model. However, explicit usage of FFT/IFFT [9], [18], [23] could not demonstrate the ability of DNN in learning waveforms.

最近的几项工作都集中在基于DL的OFDM接收器的增强上[8]，[9]。在[8]中，基于DNN的5层OFDM接收机同时实现了信道估计和调制符号恢复。他们的模型对隐藏层使用Relu激活，对输出使用sigmoid，并且均衡和恢复分2个阶段进行训练。然而，在本文中，信道均衡器和接收器是分开的，我们的接收器直接输出位而不是IQ数据。此外，[8]仅研究具有块型导频的QPSK，其中对于直接位输出的高阶调制无法复制。。在[9]中，一种基于DL的OFDM接收机据称性能优于前者。LMMSE信道估计器通过对已知模型进行初始化。然而，FFT/IFFT[9]、[18]、[23]的明确使用无法实现。展示DNN在学习波形方面的能力。

III. OFDM COMMUNICATION SYSTEM

The physical layer (PHY) of OFDM communication is introduced in this section. Specifically, the transmitter, receiver, channel process, and channel equalization in expert system are introduced to serve as the baseline of this paper.

本节将介绍OFDM通信的物理层（PHY）。具体介绍了专家系统中的发射机、接收机、信道过程和信道均衡，作为本文的基线。

A. Physical Layer

The block diagram of the PHY of OFDM communication system is illustrated in Fig. 2(a). Input bits of the OFDM transmitter is first encoded (with redundancy) to reduce errors in specific channels, the encoded bits are mapped into constellation on the In-Phase and Quadrature (IQ) plane via modulation, the resulted IQ data is represented as complex number. Pilot and guard bands are inserted to the IQ data to form frequency-domain OFDM symbol. The frequencydomain OFDM symbol is then transformed into time-domain via Inverse Discrete Fourier Transformation (IDFT), and then converted in to 1 dimensional (1D) via Parallel to Serial (P/S) conversion. Cyclic Prefix (CP), which is a section of timedomain IQ data from the end, is copied to the beginning of time-domain IQ data to form a full time-domain OFDM symbol, as shown in Fig. 2(b). The base-band IQ data stream is then up-converted to radio frequency (RF) and broadcast over-the-air by RF frontend. The radio wave propagated over wireless channel is received and down-converted into baseband digital IQ data by the RF frontend of receiver. A carrier synchronizer recovers time-domain OFDM symbols, and send it to base-band receiver. At the receiver, CP is first removed and rest of the IQ data is transformed to frequency domain via FFT. A channel equalizer estimates the responses of channel, and equalize the received IQ data distorted by the fading channel. Next, the equalized frequency-domain IQ data is demodulated to soft bits (float numbers), which are further decoded by channel decoder into binary bits. The output bit stream is sent to next layer and recovered into packets. Note that channel equalization is for fading rather than AWGN channel. Moreover, channel coding is ignored in this paper in order to focus on the lower PHY.

OFDM通信系统的PHY框图如图2(a)所示。OFDM发射机的输入位首先要进行编码（有冗余），以减少特定信道的误差，编码后的位通过调制在相位和正交（IQ）平面上映射成星座，得到的IQ数据用复数表示。在IQ数据中插入导频和保护频带，形成频域OFDM符号。频域OFDM符号通过反离散傅里叶变换(IDFT)转化为时域，再通过并行到串行(P/S)的转换转化为一维(1D)。循环前缀(Cyclic Prefix，CP)，是将时域IQ数据从末尾的一段复制到时域IQ数据的开头，形成一个完整的时域OFDM符号，如图2(b)所示。然后，基带IQ数据流被向上转换为射频(RF)，并通过RF前端进行空中广播。通过无线信道传播的无线电波被接收机的射频前端接收并下变频为基带数字IQ数据。载波同步器回收时域OFDM符号，并将其发送到基带接收器。在接收机上，首先去除CP，其余的IQ数据通过FFT转换到频域。信道均衡器估计信道的响应，并对接收到的被衰落信道扭曲的IQ数据进行均衡。接下来，经过均衡的频域IQ数据被解调为软位（浮点数），再由信道解码器将其进一步解码为二进制位。输出的比特流被送到下一层，并回收成数据包。请注意，信道均衡是针对衰减而不是加性高斯白噪声（AWGN）信道的。此外，为了关注下层PHY，本文忽略了信道编码。

OFDM communication system is usually based on physical frame composed by multiple OFDM symbols, as illustrated by an example in Fig. 2(b). The notations of parameters in a OFDM frame are defined as follows: OFDM symbol contains N subcarriers, where N is the size of IDFT at transmitter. Among these N subcarriers, there are total of G guard subcarriers at the center (DC guard band) and edge (edge guard band). A OFDM frame contains multiple consecutive OFDM symbols, which is denoted as F. A resource cell refers to a subcarrier of an OFDM symbol. For each OFDM frame, there are P cells allocated as training signals (pilot) known by both transmitter and receiver, and the rest D cells allocated to modulated IQ data. Moreover, in time domain, cyclic prefix (CP), which is a copy of a section of time-domain OFDM symbol, is added to the beginning of each OFDM symbol. As a result, the total length of time-domain OFDM symbol will be increased from N to S. These parameters are usually prescribed according to channel characteristics, such as coherence time, coherence bandwidth, and total channel bandwidth. Meanwhile, for m-ary modulation, each constellation points contains m bits, and there are 2^m constellation points.

OFDM通信系统通常基于由多个OFDM符号组成的物理帧，如图2(b)所示的一个例子。OFDM帧中参数的符号定义如下。OFDM符号包含N个子载波，其中N是发射机处IDFT的大小。在这N个子载波中，中心（DC保护带）和边缘（边缘保护带）共有G个保护子载波。一个OFDM帧包含多个连续的OFDM符号，它被表示为F，资源单元指的是一个OFDM符号的子载波。对于每个OFDM帧，有P个单元被分配为发射机和接收机都知道的训练信号(先导)，其余D个单元被分配为调制IQ数据。此外，在时域中，循环前缀（CP）是时域OFDM符号的一段副本，它被添加到每个OFDM符号的开头。因此，时域OFDM符号的总长度将从N增加到S，这些参数通常是根据信道特性规定的，如相干时间、相干带宽、总信道带宽等。同时，对于m进制调制，每个星座点包含m位，有2的m次方个星座点。

B. Wireless Channel

From the perspective of digital base-band, the wireless channel not only include over-the-air propagation between transmit and receive antennas, but also everything on the RF frontend. However, in this paper, we only consider a wireless channel with fading and noise processes, as a well accepted simplification [20]. The wireless channel is modeled as:

y = x * h + n 从数字基带的角度来看，无线信道不仅包括发射天线和接收天线之间的空中传播，还包括射频前端的一切。然而，在本文中，我们只考虑了一个有衰减和噪声过程的无线信道，这是一个公认的简化[20]。无线信道的模型为： y = x * h + n

where vectors x and y are time-domain transmitted and received signals, vector h is time domain channel coefficient, vector n is time domain white noise, and ∗ stands for convolution. (1) can also be represented in frequency domain as:
Y= X $\odot$ H + N₀

其中向量x和y为时域的发送和接收信号，向量h为时域信道系数，向量n为时域白噪声，∗代表卷积。(1)在频域中也可以表示为：

where the vector X, Y , H, and N₀ are frequency domain transformation of x, y, h, and n, e.g. X = DFT(x). N₀ is still white noise. $\odot$ stands for element wise production. Fading channel is modeled as a tapped delay line, in which channel responses, h, are a train of impulse responses [20]:

其中向量X、Y、H、是x、y、h、n的频域变换，如X=DF T(x)。 N₀ 仍旧是白噪声。$\odot$ 代表按元素相乘（两个向量的第i个元素分别相乘）。衰落信道被建模为一条分接延时线，其中信道响应h是一列脉冲响应[20]：

where the ith tap, h_i(t) is a complex number representing amplitude and phase of the ith path of signal propagation, and $\ \sum_{i=0}^{K-1}||hi(t)|| ^2 \$ = 1. The fading coefficients varies by radio environments. Fading is called slow fading if the channel coefficients keep relatively constant within a frame, vise versa fast fading. Although theoretically, channel coefficient can also change within an OFDM symbol, this situation is usually not considered based on the assumption that the OFDM frame parameters are carefully selected before hand based on prior knowledge of wireless channel.

其中，第i个抽头 h_i(t)是一个复数，代表信号传播第i条路径的振幅和相位，并且满足$\ \sum_{i=0}^{K-1}||hi(t)|| ^2 \$ = 1。衰减系数因无线电环境不同而不同。如果在一帧内信道系数保持相对恒定，则称为慢速衰减，反之则为快速衰减。虽然从理论上讲，信道系数也可以在OFDM符号内变化，但通常不考虑这种情况，因为假设OFDM帧参数是基于对无线信道的先验知识事先精心选择的。

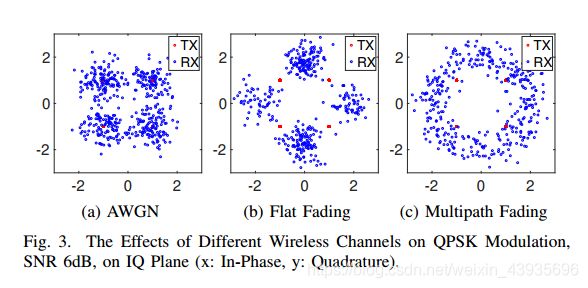
K in (3) stands for number of propagation paths in the channel. For an OFDM symbol, if K = 1, channel coefficients would be constant across all the sub-carriers, the channel is flat fading. If K > 1 (multipath), channel coefficients may vary across sub-carriers, the channel is frequency selective. In Rayleigh channel, the real and imaginary parts of follow identically independent Gaussian distributions, and ||h_i||² follows Rayleigh distribution. The effects of different fading on OFDM frame in frequency domain are illustrated in Fig. 3. Note that only noise and fading are considered, while channel impairment for channel coding is left for future works.

(3)中K代表信道中的传播路径数。对于一个OFDM符号，如果K=1，则所有子载波的信道系数将是恒定的，信道是平坦的衰减。如果K>1(多径)，各子载波的信道系数可能不同，信道具有频率选择性。在Rayleigh信道中，||h_i||² 的实部和虚部遵循完全独立的高斯分布，循Rayleigh分布。频域内不同的衰落对OFDM帧的影响如图3所示。需要注意的是，这里只考虑了噪声和衰落，而信道编码的信道损伤则留待以后的工作。

The multipath propagation introduces Inter-Symbol Interference (ISI) at the receiver, as shown in Fig. 2(b). To mitigate ISI, proper length of Cyclic Prefix is selected such that ISI from OFDM symbol i only stays in the CP of OFDM symbol i+1 in the worst cases. CP is usually dropped out at the OFDM receiver to eliminate ISI. However, not all the CP is polluted by ISI in most cases, therefore, the CP, as a redundancy of main signal, can be exploited to improve the receiver performance. This work shows that except existing analytical approaches [24]–[27], exploiting the CP to enhance receiver performance can be learned by DCCN.

如图2（b）所示，多径传播在接收机处引入了符号间干扰（ISI）。 为了减轻ISI，选择适当的循环前缀长度，使得来自OFDM符号i的ISI在最坏的情况下仅停留在OFDM符号i + 1的CP中。 通常会在OFDM接收器中丢弃CP，以消除ISI。 但是，在大多数情况下，并非所有CP都被ISI污染，因此，可以利用CP作为主信号的冗余来改善接收机性能。 这项工作表明，除了现有的分析方法[24]-[27]，DCCN可以学习利用CP来增强接收机性能。

C. Channel Estimation and Equalization

In communication system, training signal (pilot) is inserted to the frames so that the receiver could estimate the channel responses, based on the assumption that pilot and data are distorted similarly. A proper pilot pattern is designed to meet such assumption. Typical pilot patterns in OFDM system are: block, comb, and scattered, as shown in Fig. 4 [20]. The pilots could be a constant value on IQ plane, or known sequence with low auto-correlation (e.g. LTE system). The simplest channel equalization in OFDM system is based on Least Square (LS) estimator [19], [20]:

在通信系统中，将训练信号（导频）插入帧中，以便接收器可以根据导频和数据类似地失真的假设来估计信道响应。 设计了一种适当的导频模式来满足这种假设。 OFDM系统中的典型导频模式为：块，梳状和分散式，如图4所示[20]。 导频可以是IQ平面上的恒定值，也可以是具有低自相关的已知序列（例如LTE系统）。 OFDM系统中最简单的信道均衡是基于最小平方（LS）估计器[19]，[20]：

where X_P and Y_P are transmitted and received pilots in frequency domain, respectively, X_P and Y_P received data and recovered transmit data, respectively. The channel coefficients of data cells are obtained by interpolation,f(.) , of channel estimates on pilot H_P. Common interpolations include linear, spline, low-pass-filter, and DFT [19], [20]. Other estimators, such as Minimum Mean Square Error (MMSE), Linear MMSE (LMMSE), Maximal likelihood, and parametric channel modeling-based (PCMB) estimator, are based on LS estimation and/or prior channel knowledge [19], [20].

其中X_P和Y_P分别在频域中发送和接收导频，X_P和Y_P分别是接收数据和恢复的发送数据。通过导频上H_P信道估计的插值f(.)获得数据单元的信道系数。常见的插值包括线性插值、样条插值、低通滤波和DFT[19]、[20]。其他估计器，如最小均方误差（MMSE）、线性MMSE（LMMSE）、最大似然和基于参数信道建模（PCMB）的估计器，基于LS估计和/或先验信道知识[19]、[20]。

IV. DCCN-BASED OFDM RECEIVER

In this section, the design and training approaches of the Deep Complex Convolutional Network (DCCN)-based OFDM receiver are introduced. The DCCN-based OFDM receiver contains a basic OFDM receiver without channel equalization, and a separate channel equalizer. The design of the basic OFDM receiver and channel equalizer are inspired by expert OFDM receiver and LS channel equalizer. Therefore, the design of flow-graph is described as function blocks of expert OFDM receiver and LS channel equalizer. However, the actual behavior of each layer of a trained model may be different from the designed purpose. Rather than specifying the functionality of each layer, this design approach is to ensure a basic LS estimator is at least in the search space of deep learning by leveraging field knowledge. In fact, the design is to contain rich computational redundancy, hoping that some unknown solution or phenomenon may be learned or discovered. After training, most redundancy would be removed, and skip connection structure is to give the DCCN model maximal flexibility to achieve best performance.

介绍了基于深复卷积网络（DCCN）的OFDM接收机的设计和训练方法。基于DCCN的OFDM接收机包含一个基本的没有信道均衡的OFDM接收机和一个独立的信道均衡器。基本OFDM接收机和信道均衡器的设计灵感来自于专家OFDM接收机和LS信道均衡器。因此，将流程图的设计描述为专家OFDM接收机和LS信道均衡器的功能模块。然而，训练模型的每一层的实际行为可能与设计目的不同。这种设计方法不是指定每一层的功能，而是通过利用领域知识确保基本LS估计器至少在深度学习的搜索空间中。实际上，这种设计是为了包含丰富的计算冗余，希望能够学习或发现一些未知的解或现象。训练完成后，大部分冗余将被消除，跳转连接结构是为了给DCCN模型以最大的灵活性，以达到最佳的性能。

A. Complex Layers

Currently (Oct, 2018), complex neuron network is not yet supported by popular Deep Learning platforms. For example, Tensorflow [16] and Keras [17] only supports untrainable complex operations, such as FFT, and IFFT, but not supports complex numbers in trainable Neuron Network layers, like fully-connected (FC), and convolutional (Conv) layers. The construction of complex neuron networks is addressed in [28].The major concern is complex multiplication：

目前（2018年10月），复数神经元网络尚未得到流行的深度学习平台的支持。例如，Tensorflow[16]和Keras[17]只支持不可训练的复数运算，如FFT和IFFT，但不支持可训练神经元网络层中的复数，如完全连接（FC）和卷积（Conv）层。复数神经元网络的构造在[28]中有论述。主要的问题是复数乘法：

For a minimal FC complex layer with input and output both of size 1, consider its input as a + bi and weight as c + di. Based on (5), the complex FC layer can be implemented by real FC layer with input and output both of size 2. The 4 weights of the real FC layer are able to be trained to be c, −c, d, −d. Therefore, a real FC layer is capable of implementing a complex FC layer of half size. A complex Conv layer can be implemented by a higher dimensional real conv layer with double filters [1]. As illustrated in Fig. 5, an 1D complex Conv layer of size 8 × 8 × 1 (which stands for 8 filters, each with a size of 8, and channel of 1) can be implemented by a 2D real conv layer of size 16 × (1;8) × 1. In this work, real and imaginary parts of a complex tensor are in the last dimension.

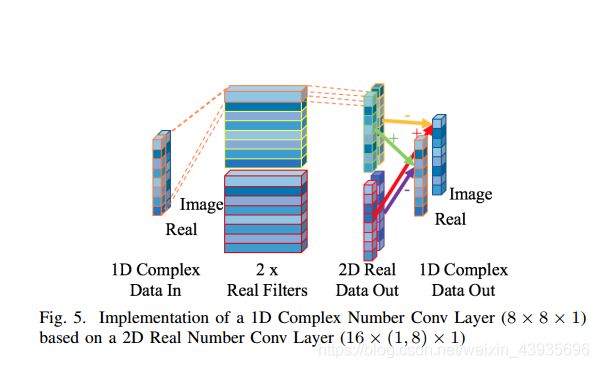
对于输入和输出都为1的最小FC复数层，考虑其输入为a+bi，权重为c+di。在（5）的基础上，复数的FC层可以由输入输出均为2的实际FC层实现。真实FC层的4个权重可以训练为c、−c、d、−d。因此，真实FC层能够实现一半大小的复数FC层。一个复数的Conv层可以由一个高维的实数Conv层来实现，它带有两个滤波器[1]。如图5所示，尺寸为8×8×1的1D复数Conv层（表示8个滤波器，每个滤波器的尺寸为8，信道为1）可以通过尺寸为16×1（1；8）×1的2D实Conv层来实现。在这项工作中，复张量的实部和虚部都在最后一个维中。

Digital Signal Processing in OFDM system is generally linear transformation (on complex numbers). Moreover, the real and imaginary parts of IQ data are in both positive and negative regimes. Therefore, we only use tanh activations for IQ data by treating a complex number as two independent real numbers. Non-linear operations are between bit and IQ domains, such as modulation and demodulation. In demodulation, IQ data is simply viewed as 2 real numbers, and Leaky Rectified Linear Unit (LRelu) is used only for real numbers.

OFDM系统中的数字信号处理一般是线性变换（关于复数）。此外，IQ数据的实部和虚部都处于正态和负态。因此，我们只对IQ数据使用tanh激活，把一个复数当作两个独立的实数。非线性操作是在比特域和IQ域之间进行的，例如调制和解调。在解调中，IQ数据被简单地看作2个实数，而漏整流线性单元（LRelu）仅用于实数

B. Basic DCCN Receiver

The basic DCCN receiver is an OFDM receiver without channel equalizer. The flow graph of basic DCCN receiver is illustrated in Table I. The DCCN receiver model contains three parts: the first part includes first 3 layers, which is intended to transform time domain OFDM symbol into frequency domain. The major component of the first part is a Complex Conv (C-Conv) layer of size N × S(N) × 1. The basic DCCN receiver can take in or drop CP by configuration. Dropping CP is implemented by an optional slice operation before the C-Conv layer. The second part contains layers 4 to 6, which is intended to extract all the data cells of an OFDM frame, this is implemented by a FC layer. Parts 1 and 2 parts are for processing IQ data (complex number), of which the real and imaginary parts are stored in the last dimension of tensors. Part 3 is for demodulation, which is convert the complex IQ data into soft bits. Part 3 treat the real and imaginary parts of complex IQ data as 2 channels of real number. The IQ data is fed to 2 Real Conv (R-Conv) layers with 2m filters, followed by a LRelu activation. A skip connection is designed to combine the original IQ data and the output of LRelu activation, and feed them together to a final FC layer. The FC layer is followed by an LRelu activation and then an softmax activation. The output of softmax activation are soft bits, which represents each bit with 2 real numbers (e.g. Log-Likelihoods of 0 and 1)

基本的DCCN接收机是一个没有信道均衡器的OFDM接收机。基本DCCN接收机的流程图如表1所示。DCCN接收机模型包括三个部分：第一部分包括前3层，用于将时域OFDM符号转换为频域。第一部分的主要组成部分是一个复数的Conv（C-Conv）层，大小为N×S（N）×1。基本的DCCN接收器可以根据配置接收或丢弃CP。删除CP是通过在C-Conv层之前的可选切片操作来实现的。第二部分包括第4到第6层，用于提取OFDM帧的所有数据单元，这是由FC层实现的。第1部分和第2部分用于处理IQ数据（复数），其中实部和虚部存储在张量的最后一个维度中。第三部分是解调，它将复数的IQ数据转换成软比特。第3部分将复IQ数据的实部和虚部视为2个实数通道。IQ数据通过2m滤波器送入2个真实的Conv（R-Conv）层，然后激活LRelu。跳转连接被设计成将原始的IQ数据和LRelu激活的输出相结合，并将它们一起提供给最终的FC层。FC层之后是LRelu激活，然后是softmax激活。softmax激活的输出是软位，用2个实数表示每个位（例如0和1的对数似然）

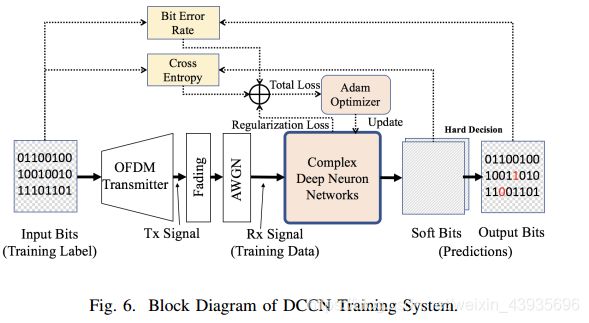
Since channel coding is out of the scope of this paper, we simply use hard decision to get output bits from the soft bits. The cross entropy and bit error rate (BER) are then calculated from soft bits and output bits by comparing with input bits. The cross entropy and BER are used to construct loss function for training of the DCCN models, as shown in Fig. 6.

由于信道编码不在本文的讨论范围之内，我们只需使用硬判决从软比特中获取输出比特。然后根据软比特和输出比特与输入比特进行比较，计算出交叉熵和误码率（BER）。交叉熵和误码率被用来构造训练DCCN模型的损失函数，如图6所示。

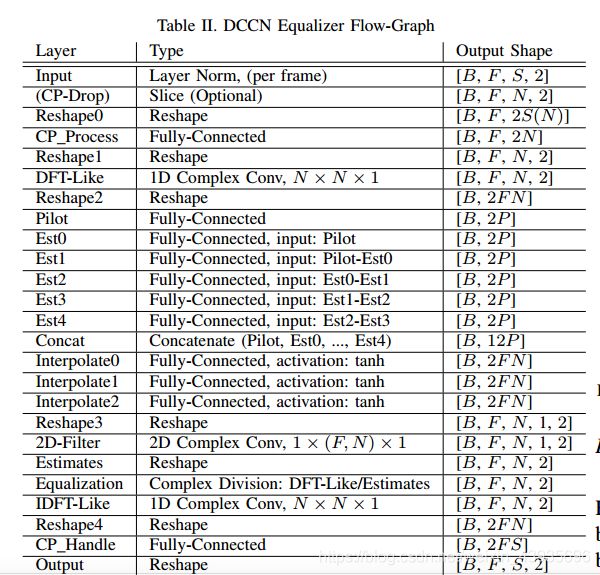
C. DCCN Channel Equalizer

The channel equalizer of OFDM receiver is usually located in frequency domain, (Fig. 2(a)) to avoid convolution operation. In this work, a standalone equalizer is designed before the basic receiver for the convenience of implementing transfer learning (detailed in Section IV-D) in Tensorflow [16]. The flow graph of the equalizer, as presented in Table II, contains 4 parts by design. The first (layer 0-5) and fourth parts (last 4 layers) are DFT/IDFT-like complex Conv layers intended to perform time/frequency domain transformation. Notice that in part 1, a FC layer is placed before the DFT-Like layer to process CP. In part 4, the IDFT-Like layer is followed by a FC layer for adding back CP. Part 2, from layers 6 to 19, is for channel estimation. Part 3, layer 20, is frequency domain channel equalization implemented by complex division: the output of part 1 (frequency domain receive signal) over the output of part 2 (channel estimates)

为了避免卷积运算，OFDM接收机的信道均衡器通常位于频域（图2（a））。在这项工作中，在基本接收机之前设计了一个独立的均衡器，以便在Tensorflow[16]中实现传输学习（详见第IV-D节）。如表二所示，均衡器的流程图由4部分组成。第一部分（第0-5层）和第四部分（最后4层）是用于执行时域/频域变换的类似DFT/IDFT的复数Conv层。请注意，在第1部分中，FC层放在类DFT层之前以处理CP。在第4部分中，类似IDFT的层后面是FC层，用于添加回CP。第2部分（从第6层到第19层）用于信道估计。第3部分，第20层，是通过复除法实现的频域信道均衡：第1部分（频域接收信号）的输出超过第2部分（信道估计）的输出

In part 2, the channel estimator, the first step is extract pilot in a frame with FC layer, followed by a FC layer for LS estimation. Next, 4 layers of FC layers are followed to estimate the residual of previous estimation. The layers of pilot, 1st order LS estimation, and 4 residual estimations are all fed into next Interpolation block through a skip connection structure (Concat). The interpolation block contains 3 FC layers with tanh activation of full frame size, followed by a 2D complex Conv layer of size 1 × (F; N) × 1 (1 fiter with size (F; N) and 1 channel), as 2D-Filter. The output of the 2D Filter is reshaped to match the size of frequency domain signal from part 1. Through experiments, we found that similar model without the residual components and skip connections would have significantly worse performance.

在第二部分信道估计器中，第一步是在具有FC层的帧中提取导频，然后在FC层中进行LS估计。接下来，跟踪4层FC层来估计先前估计的残差。导频层、一阶LS估计和4个残差估计均通过跳接结构（Concat）送入下一个插值块。内插块包含3个FC层，具有全帧大小的tanh激活，然后是尺寸为1×（F；N）×1（1个fiter with size（F；N）和1个通道）的2D复Conv层，作为2D滤波器。对2D滤波器的输出进行整形，以匹配第1部分中的频域信号的大小。通过实验，我们发现相似的模型如果没有残差分量和跳跃连接，性能会明显变差。

For a particular CP option, the same DCCN flow graph is used for all modulations and fading settings, but trained separately, hence end with different parameters. The only difference between CP options is whether or not dropping the CP in part 1 of the DCCN equalizer flow-graph.

对于特定的CP选项，相同的DCCN流图用于所有调制和衰落设置，但单独训练，因此以不同的参数结束。CP选项之间的唯一区别是是否在DCCN均衡器流图的第1部分中删除CP。

D. 2-Stage Training

The training setting of DCCN receiver, as illustrated in Fig. 6, contains an online random generator creating random bits as training labels, a OFDM transmitter translate input bits into time domain OFDM symbols (transmit (Tx) signal). A channel model adds fading and noise to the Tx signal to create receive (Rx) signal. The Rx signal is the training data fed into the DCCN model. The output of DCCN model are soft bits, and output bits are generated by hard decision. The cross entropy and BER are calculated based on training labels and predictions (Soft bits and output bits). The total loss, L, is calculated by sum of the cross entropy (CE), logarithmic BER, and regularization loss © of the model:

两个阶段的训练

如图6所示，DCCN接收机的训练设置包含在线随机发生器，其创建随机比特作为训练标签，OFDM发射机将输入比特转换为时域OFDM符号（发送（Tx）信号）。信道模型在发送信号中加入衰落和噪声以产生接收（Rx）信号。接收信号是输入DCCN模型的训练数据。DCCN模型的输出为软比特，输出比特由硬判决产生。交叉熵和误码率是根据训练标签和预测（软比特和输出比特）计算的。总损耗L由模型的交叉熵（CE）、对数BER和正则化损失（L_reg）之和计算：

The logarithmic BER could prevent diminishing gradient due to tiny changes of CE when BER is very small. With the loss function, Adam optimizer runs back-propagation to optimize randomly initialized DCCN model during training.

当误码率很小时，对数误码率可以防止由于CE的微小变化而导致的梯度减小。利用损失函数，Adam优化器在训练过程中对随机初始化的DCCN模型进行反向传播优化。

The equalized DCCN receiver is too complex to be trained together at one time. At best, it takes several times longer than training them separately. Most likely, it never start to converge. Therefore, transfer learning is adopted to train the DCCN receiver and equalizer in two stages, as illustrated in Fig. 7. In stage 1, the basic DCCN receiver is trained in AWGN channel. Fading is removed from channel model in the generation of training data, Rx Signal. When training is completed, the trained DCCN receiver (flow graph with parameters) is saved, and the TensorFlow session is closed. In stage 2, a second TensorFlow session is first initialized for graph-editing. The pre-trained basic DCCN receiver is loaded, and a new model of DCCN Equalizer is built and inserted before the trained DCCN receiver. Then, the edited flow-graph is saved and the second session is closed because graph editing and training have to be in different sessions. After that, a third session is initialized and the previous flow graph is loaded for training. The same cost function is used in stages 1 and 2. At stage 2, fading is included in the generation of training data, and only the DCCN equalizer is trained. The graph-editing technique enables the DCCN receiver to pass the gradients in back-propagation without being updated in stage 2.

均衡DCCN接收机过于复数，不能同时训练在一起。充其量，这比单独训练他们所花的时间要长几倍。最有可能的是，它从未开始收敛。因此，如图7所示，采用转移学习来分两个阶段训练DCCN接收器和均衡器。在第一阶段，基本的DCCN接收机在AWGN信道中训练。在训练数据Rx信号的生成过程中，去除了信道模型中的衰落。训练完成后，保存训练的DCCN接收器（带参数的流图），并关闭TensorFlow会话。在第2阶段中，首先初始化第二个TensorFlow会话以进行图形编辑。加载预先训练好的基本DCCN接收机，并在训练好的DCCN接收机之前建立并插入一个新的DCCN均衡器模型。然后，保存编辑的流程图并关闭第二个会话，因为图形编辑和培训必须在不同的会话中进行。然后，初始化第三个会话，并加载上一个流图进行训练。第1阶段和第2阶段使用相同的损失函数。在第二阶段，训练数据的产生包括衰落，并且只训练DCCN均衡器。图形编辑技术使DCCN接收机能够在反向传播中通过梯度，而无需在第2阶段中更新。

To improve the training efficiency, several techniques are used. First, the training data is fed to the model in mini batches. The batch size is set to 512 OFDM symbols (64 OFDM Frames). With mini-batch technique, we could leverage the high throughput parallel processing capability of GPU, while minimize its high IO latency. Second, in the programming of NumPy-based OFDM transmitter and fading modules, data processing are vectorized and large loops are avoided. Third, the learning rate is set to 0.001 initially and decay exponentially every 2.5 episodes. This ensures a smaller learning rate for fine-tuning the model at later phase of training. Beside setting a maximum number of training
episodes, we also set an early stop mechanism to end the training if key performance metric (BER) was not improved in a fixed window of most recent episodes. Notice that since we could not use all the possible training labels (246m bits) for training, but generate random bits for each episode, we use episode instead of epoch (an iteration that all training data went through once) throughput this paper.

为了提高训练效率，采用了几种技巧。首先，将训练数据分批输入模型。批处理大小被设置为512个OFDM符号（64个OFDM帧）。利用小批量技术，我们可以利用GPU的高吞吐量并行处理能力，同时最小化其高IO延迟。其次，在基于NumPy的OFDM发射机和衰落模块的编程中，对数据进行了矢量化处理，避免了大的环路。第三，初始学习率设为0.001，每2.5集呈指数衰减。这保证了在后期的训练阶段，对模型进行微调的学习速度更小。除了设置最大训练集数之外，我们还设置了一个早期停止机制，如果在最近几集的固定窗口内关键性能指标（BER）没有改善，则结束训练。注意，由于我们不能使用所有可能的训练标签（246兆比特）进行训练，而是为每一集生成随机位，因此本文使用了episode而不是epoch（所有训练数据经过一次迭代）的吞吐量。

E. Training Signal-to-Noise Ratio

There is no clear guidance of setting the training SNR for a DL-based PHY. SNR of 5dB is recommended in [3]. In this paper, we found that relatively low training SNR (e.g. 3dB EbNo) generally helps to achieve better performance with less training. Noise helps to regularize Artificial Neural Networks to avoid over-fitting. However, only low training SNR may hide some flaws of the model. For example, a flawed model maybe trained to contain an small systematic error which outputs slightly more 1s than 0s. At lower SNRs, this systematic error is hidden by relatively large BER. However, such bias will persist and cause a BER floor in high SNR regime.

训练信噪比
对于基于DL的PHY，如何设置训练SNR没有明确的指导。[3]中建议信噪比为5dB。在本文中，我们发现相对较低的训练信噪比（例如3dB EbNo）通常有助于在较少的训练下获得更好的性能。噪声有助于正则化人工神经网络，以避免过度拟合。然而，只有低的训练信噪比才能掩盖模型的一些缺陷。例如，一个有缺陷的模型可能被训练成包含一个小的系统误差，输出的1s比0s稍多，在低信噪比下，这个系统误差被相对较大的误码率所掩盖。然而，这种偏差将持续存在，并在高信噪比下造成误码率下限。

To minimize systematic error, a combination of low and high SNR setting are used in training. For m-ary modulation, the base SNR is set as 3m dB. At stage 1, for every 8 OFDM frames, there are 4 frames with SNR of 3m dB, 1 frame of 3m−3 dB, and 3 frames of 3m+5 dB. This combination helps to improve the training efficiency while minimize systematic errors. At stage 2, the SNR offsets are [−3; 0; 0; 3; 6; 9; 12; 17] dB for every 8 OFDM frames in training. Under this configuration, the channel estimator is exposed to a wide range of SNR during training. This is because pilot signal carries different amount of channel information at different SNRs, channel estimator trained at a narrow range of SNR is more likely to be over-fitted to a specific SNR range.

为了减小系统误差，训练中采用了低信噪比和高信噪比设置相结合的方法。对于m进制调制，基本信噪比设为3m dB。在第1阶段，每8个OFDM帧中，有4个帧的信噪比为3m dB，1个帧的信噪比为3m−3db，3个帧的信噪比为3m+5db。这种组合有助于提高训练效率，同时最大限度地减少系统误差。在第2阶段，训练中每8个OFDM帧的SNR偏移为[−3；0；0；3；6；9；12；17]dB。在这种结构下，信道估计器在训练过程中会受到很大的信噪比影响。这是因为导频信号在不同的信噪比下携带了不同数量的信道信息，在较窄信噪比范围内训练的信道估计器更容易过拟合到特定的信噪比范围

V. EVALUATION RESULTS

The performance of DCCN receiver is evaluated by its biterror-rate (BER) in different channel and SNR settings. First, the BER of basic DCCN receiver in Additive Gaussian White Noise (AWGN) channel is presented, followed by the BER of equalized DCCN receiver in two Rayleigh fading channels: flat fading and multipath fading. m-QAM modulation (m ≤ 4)are evaluated. There are 2 options for the basic and equalized DCCN receivers: with and without Cyclic Prefix. A model for each modulation and CP option is built, trained, and tested. The DCCN receivers are benchmarked by an expert OFDM receiver, as shown in Fig. 2(a), implemented in Matlab [29].

在不同的信道和信噪比条件下，通过误码率（BER）来评估DCCN接收机的性能。首先给出了基本DCCN接收机在加性高斯白噪声（AWGN）信道中的误码率，然后分析了在平坦衰落和多径衰落两种瑞利衰落信道下的均衡DCCN接收机的误码率。对m-QAM调制（m≤4）进行了评估。基本和均衡DCCN接收机有2个选项：有和没有循环前缀。建立、训练和测试每个调制和CP选项的模型。DCCN接收机由专家OFDM接收机进行基准测试，如图2（a）所示，在Matlab中实现[29]。

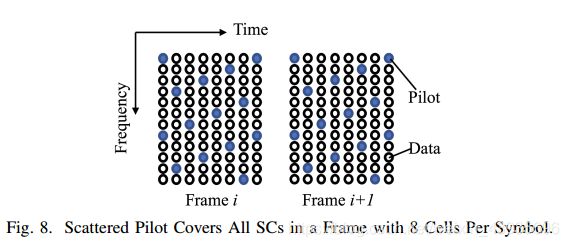
The OFDM system and fading channel are configured as in Table III. The sample rate is 10Mbps. An OFDM frame contains 8 OFDM symbols with FFT size of 64 and Cyclic Prefix (CP) length of 16. Each OFDM symbol has 10 guard subcarriers (SCs) including Direct Current (DC), 8 pilot SCs and 46 data SCs. The numbers of pilot and data cells in each frame are 64 and 368, respectively. Pilots are scattered and spread across all non-guard SCs, as illustrated in Fig. 8. This pilot pattern is efficient in spectrum resources, and ensures consistent performance of benchmark channel estimation algorithms, as apposed to other types [8]. Each pilot has value of 1 + 1i. The maximal power of the constellation for a given modulation is normalized to pilot power. Gray code is applied for mapping between constellation and bits. After the transmitter, the Peak to Average Power Ratio (PAPR) of OFDM waveform is limited to 9dB. The AWGN and Rayleigh channels are tested. Fading channel includes flat fading and multipath fading, the latter is Extended Pedestrian A model (EPA) from 3GPP [30]. Slow fading is considered, in which the channel taps are updated per frame. With EPA model, there would be InterSymbol Interference (ISI) within a frame, but no ISI across frames which could be eliminated by the gap slot between 2 frames. The delay spread of EPA model (450 ns) is shorter than CP (1600 ns). For simplicity, perfect synchronization is considered at receiver, so that time and frequency offsets, as well as Doppler shifts are ignored, which are already addressed in [2], [6]. This configuration emulate a baseline scenario of LTE system. For fading channel, the noise power is set according to SNR based on the average signal power of 64 OFDM frames (512 OFDM Symbols).

OFDM系统和衰落信道配置如表III所示，采样率为10Mbps。一个OFDM帧包含8个OFDM符号，FFT大小为64，循环前缀（CP）长度为16。每个OFDM符号有10个保护子载波（SCs），包括直流（DC）、8个导频SCs和46个数据SCs。每帧中的导频和数据单元的数目分别为64和368。如图8所示，飞行员分散分布在所有非防护SCs上。这种导频模式在频谱资源方面是有效的，并确保基准信道估计算法的一致性能，与其他类型的导频模式相同[8]。每个导频的值为1+1i。给定调制下星座的最大功率被归一化为导频功率。采用灰色编码实现星座与位之间的映射。发射后，OFDM波形的峰均功率比（PAPR）被限制在9dB。对AWGN和Rayleigh信道进行了测试。衰落信道包括平坦衰落和多径衰落，后者是3GPP[30]提出的扩展行人A模型（EPA）。考虑慢衰落，信道抽头每帧更新一次。在EPA模型下，帧内存在码间干扰（ISI），而帧间没有码间干扰，可以通过帧间的缝隙来消除。EPA模型（450ns）的延迟扩展比CP（1600ns）短。为了简单起见，在接收机处考虑了完全同步，因此忽略了时间和频率偏移以及多普勒频移，这在[2]，[6]中已经讨论过。该配置模拟了LTE系统的基线场景。对于衰落信道，根据64个OFDM帧（512个OFDM符号）的平均信号功率，根据SNR设置噪声功率。

The configurations for the training of DCCN receiver and equalizer with m-ary modulation are detailed in Table IV. Stochastic gradient descent-based Adam optimizer with mini batch size of 64 frames are used. For each episode, a new random bit stream (training labels) is generated and converted into corresponding training data by expert OFDM transmitter and channel model. Since training labels are completely random, the total cost for early stop is based on training data rather than a separate test data set. The training ends either when reach to the maximum number of episodes, or the total cost was not improved over the most recent 100 episodes (early stop window). The learning rate is set to 0.001 initially and decayed by 2% every 500 steps or 2.5 episodes. SNR is set per frame based on baseline SNR of 3mdB with different ∆ values per 8 frames. Each training episode contains 200 mini batches, and testing bits of 2000 frames for each of 40 SNR points (-10 to 29 dB with 1dB step)

OFDM系统和衰落信道配置如表III所示，采样率为10Mbps。一个OFDM帧包含8个OFDM符号，FFT大小为64，循环前缀（CP）长度为16。每个OFDM符号有10个保护子载波（SCs），包括直流（DC）、8个导频SCs和46个数据SCs。每帧中的导频和数据单元的数目分别为64和368。如图8所示，飞行员分散分布在所有非防护SCs上。这种导频模式在频谱资源方面是有效的，并确保基准信道估计算法的一致性能，与其他类型的导频模式相同[8]。每个导频的值为1+1i。给定调制下星座的最大功率被归一化为导频功率。采用灰色编码实现星座与位之间的映射。发射后，OFDM波形的峰均功率比（PAPR）被限制在9dB。对AWGN和Rayleigh信道进行了测试。衰落信道包括平坦衰落和多径衰落，后者是3GPP[30]提出的扩展行人A模型（EPA）。考虑慢衰落，信道抽头每帧更新一次。在EPA模型下，帧内存在码间干扰（ISI），而帧间没有码间干扰，可以通过帧间的缝隙来消除。EPA模型（450ns）的延迟扩展比CP（1600ns）短。为了简单起见，在接收机处考虑了完全同步，因此忽略了时间和频率偏移以及多普勒频移，这在[2]，[6]中已经讨论过。该配置模拟了LTE系统的基线场景。对于衰落信道，根据64个OFDM帧（512个OFDM符号）的平均信号功率，根据SNR设置噪声功率。

Training a DCCN model takes from 250 to 1300 episodes, as shown in Fig. 9. The training process starts with a quick fitting followed by a long fine-tuning phase: the cross entropy decreases drastically in the first 10-50 episodes, then slowly but steadily until hitting a floor.

训练DCCN模型需要250到1300集，如图9所示。训练过程从快速适应开始，然后是一个长时间的微调阶段：交叉熵在前10-50集急剧下降，然后缓慢但稳定地下降，直到触底。

A. Additive Gaussian White Noise Channel

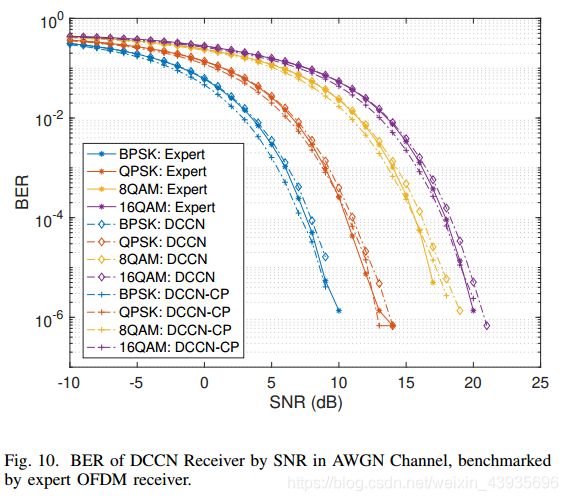
The BER performance of basic DCCN receivers in AWGN channel over the full range of testing SNR is presented in Figs. 10. The benchmark is Matlab-based expert OFDM receiver without equalizer [29]. The basic DCCN receiver with CP outperforms the benchmark, while DCCN without CP slightly underperforms in high SNRs.

加性高斯白噪声信道
图中给出了在AWGN信道中基本DCCN接收机在整个测试信噪比范围内的误码率性能。10基准是基于Matlab的无均衡器的专家OFDM接收机[29]。具有CP的基本DCCN接收器的性能优于基准，而不带CP的DCCN接收器在高SNR中的表现稍差。

For DCCN receiver without CP, denoted as DCCN, the BER performance is 0.3 to 0.8dB worse than the benchmark at high SNRs. Note that when BER is very small, e.g ≤ 10⁻⁵, it is more subjected to randomness due to limited test data size. For DCCN receiver with CP, denoted as DCCNCP, the BER performance is 0.4 to 0.8 dB better than the benchmark, but the improvement diminishes in high SNRs (EbNo ≥ 5dB). As a redundancy of time-domain OFDM waveform, CP carries some information for all subcarriers while experience independent random noise. Theoretically, CP could improve the signal power by CP=N, translated into 0.97dB of improvement in AWGN with our configuration. The test BER of DCCN-CP receiver is about 0.7-0.97 dB better than the DCCN receiver. It can be observed that DCCN of 8-QAM is slightly worse than other modulations in high SNRs. This is probably because 8-QAM constellation is less symmetric than the other 3 modulations.

对于没有CP的DCCN接收机，表示为DCCN，在高信噪比下，误码率性能比基准差0.3～0.8dB。注意，当误码率很小时，例如≤10⁻⁵，由于测试数据大小有限，它更容易受到随机性的影响。对于具有CP的DCCN接收机，表示为DCCNCP，其误码率性能比基准提高了0.4～0.8db，但在高信噪比（EbNo≥5dB）时，性能改善有所减弱。作为时域OFDM波形的一种冗余，CP在经历独立的随机噪声的同时，携带了所有子载波的一些信息。理论上，CP可以通过CP=N提高信号功率，转化为AWGN中0.97dB的改善。DCCN-CP接收机的测试误码率比DCCN接收机高0.7-0.97分贝。与其它调制方式相比，snqars的调制效果稍差。这可能是因为8-QAM星座比其他3种调制方式对称性差。

B. Rayleigh Fading Channels

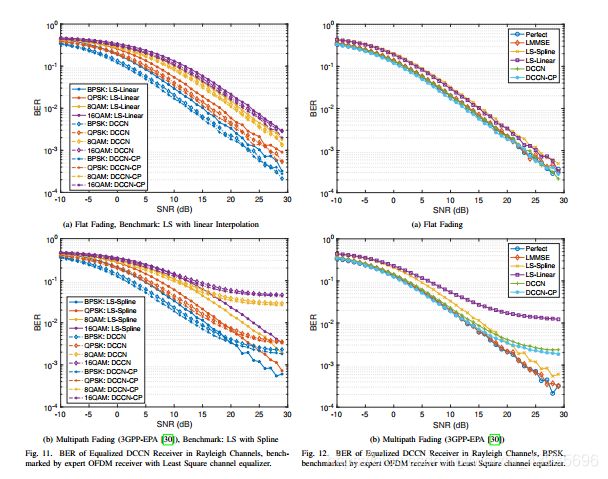
The equalized DCCN receivers are benchmarked by expert OFDM receiver with LS estimators, with 2D linear (flat fading) and 2D Spline (EPA) interpolations, as shown in Figs. 11. In multi-path fading, Spline outperforms linear interpolation, and vise versa in flat fading, as shown in Figs. 12. The BER of equalized DCCN receivers by SNR in flat fading channel is presented in Fig. 11(a). The equalized DCCN receiver significantly outperforms benchmark in BPSK modulation by 2 to 2.5 dB w/o CP and 2.5 to 3 dB w/ CP. For QPSK, the improvement is 1 to 2 dB w/o CP and 2 to 2.8 dB with CP. For 8QAM and 16QAM, equalized DCCN outperforms benchmark by 0.5 to 1 dB w/o CP and 0.8 to 1.5 dB w/ CP. The improvement also varies by SNR: the DCCN outperforms benchmark by 3 to 5dB in the negative SNR regime, while the advantage slightly reduced in high SNR regime (≥ 24dB). The performance deterioration of DCCN in high SNR regime is contributed by both basic receiver and the equalizer. Generally, the DCCN performs consistently in simple flat fading channel and has advantages in low SNRs

瑞利衰落信道
均衡DCCN接收机由具有LS估计的专家OFDM接收机进行基准测试，采用2D线性（平坦衰落）和2D样条（EPA）插值，如图所示。11在多径衰落中，样条函数的性能优于线性插值，而在平坦衰落中，样条曲线的性能则相反。12图11（a）给出了在平坦衰落信道中，通过SNR均衡DCCN接收机的误码率。均衡DCCN接收机在BPSK调制方面的性能明显优于基准，分别为2~2.5dB w/o CP和2.5~3dB w/CP。QPSK在8QAM和16QAM下的性能分别提高了1_2dB和22.8dB，均衡DCCN的性能优于基准，分别为0.5到1 dB w/o CP和0.8到1.5 dB w/CP。这种改善也因信噪比而异：DCCN在负信噪比条件下比基准高3-5dB，而在高信噪比条件下（≥24dB）优势略有下降。DCCN在高信噪比下的性能恶化是由基本接收机和均衡器共同造成的。一般来说，DCCN在简单平坦衰落信道中性能稳定，在低信噪比下具有优势。

The BER of equalized DCCN receivers by SNR in frequency selective channel (3GPP EPA model [30]) is presented in Fig. 11(b). For BPSK and QPSK in middle to low SNR regimes (≤ 15dB), equalized DCCN receivers still significantly outperform LS Spline by mostly 1.8 to 2.3 dB w/o CP, and 2 to 3 dB w/ CP. However, when SNR ≥ 18dB, the BER of equalized DCCN gradually reach a floor and underperforms the benchmark. For 8QAM and 16 QAM, however, the equalized DCCN only slightly outperforms the benchmark in low SNRs (≤ 9dB), while significantly underperform the benchmark in middle to high SNRs (≥ 9dB). Further examination shows there is systematic error in DCCN that causes the BER floor. It shows that in complex fading, the DCCN performs worse in high SNRs and higher modulation orders.

图11（b）给出了频率选择性信道（3GPP-EPA模型[30]）中通过SNR均衡的DCCN接收机的误码率。对于中低信噪比（≤15dB）的BPSK和QPSK，均衡DCCN接收机的性能仍明显优于LS样条，分别为1.8～2.3db和2～3db，但当信噪比≥18dB时，均衡DCCN的误码率逐渐达到一个下限，并低于基准。然而，对于8QAM和16qam，均衡DCCN在低信噪比（≤9dB）中仅略优于基准，而在中高信噪比（≥9dB）中则明显低于基准。进一步的检查表明DCCN中存在系统误差，导致误码率下限。结果表明，在复衰落中，DCCN在高信噪比和高调制阶数下表现较差。

In Figs. 12, the BER of equalized DCCN receivers with BPSK is further compared to equalizers with perfect channel state information, as well as LMMSE, LS-Linear, and LSSpline estimators. In flat fading (Fig. 12(a)), for SNR ≤ 13dB, equalized DCCN receivers w/o CP only slightly underperforms perfect equalizer by around 0.3 dB for DCCN (slightly outperform LMMSE based on perfect SNR by ignorable margin), while DCCN w/ CP slightly outperform perfect equalizer by about 0.5 dB. In EPA channel (Fig. 12(b)), for SNR ≤ 13dB, the equalized DCCN receivers w/o CP under-performs the perfect equalizer (which is almost the same as LMMSE based on perfect SNR) by 0.5 to 1 dB, and DCCN w/ CP slightly outperforms perfect equalizer by up to 0.3 dB. It shows that DCCN is very close to perfect equalizer for BPSK without prior channel knowledge from middle to very low SNRs. On the other hand, both DCCN and LS-Linear equalizer exhibits BER floors, which implies that DCCN may belong to the
family of linear but cubic interpolation.

在图12中进一步比较了带BPSK的DCCN均衡接收机的误码率与具有完全信道状态信息的均衡器以及LMMSE、LS线性和LSSpline估计量。在平坦衰落（图12（a））中，对于SNR≤13dB，对于DCCN，不带CP的均衡DCCN接收机的性能仅略低于完美均衡器约0.3db（在可忽略裕度上略优于基于完美SNR的LMMSE），而带CP的DCCN接收机略优于完美均衡器约0.5db。在EPA信道（图12（b））中，对于SNR≤13dB，不带CP的均衡DCCN接收机执行完美均衡器（几乎与基于完美SNR的LMMSE几乎相同）0.5到1db，并且DCCN w/CP稍微优于完美均衡器高达0.3db。结果表明，在没有先验信道知识的情况下，DCCN在中、低信噪比的情况下，接近于BPSK的理想均衡器。另一方面，DCCN和LS线性均衡器都具有误码率下限，这意味着DCCN可能属于线性三次插值族。

C. Alternative Structures of Basic DCCN Receiver

To understand the contribution of layer(s) in the basic DCCN receiver, 7 alternative structures of the original model, (a–g), are explored by replacing and/or removing certain layer(s), as listed in Table V (– means the same as original). The BER performance of the 7 alternative basic DCCN receivers for 16QAM are presented in Fig. 13. Similar results are found in 8QAM, while all alternatives perform identically well in BPSK and QPSK. Except c and d, rest of the alternatives performs almost identically to the original basic DCCN receiver. In alternatives a and g, the DFT-Like C-Conv layer in original model is replaced by a FC layer, the fact that a and g achieve the same performance of original DCCN implies that FC layer is able to perform DFT transformation as a C-Conv
layer. In alternatives b and g, the R-Conv layers are removed, such that a combination of IQ data and LRelu-activated IQ data are fed into the last demodulation FC layer. They show that the R Conv layers do not contribute to demodulation. However, R-Conv layers could accelerate the training. Alternatives e shows that the last LRelu activation can be replaced by linear activation without harming performance. In alternatives c and d, the R-Conv and the skip connection are removed so that either the IQ data © or LRelu-activated IQ data (d) are fed into the demodulation FC layer. The result shows that a FC layer could not perform demodulation based only on either IQ data or non-linear activated IQ data for higher modulationorder. Alternative f also removes the skip connection, but, R-Conv layers with 2m filters are in-place to pick out each constellation point. Alternative f shows that the R-Conv layers with non-linear activation could replace the skip connection.

基本DCCN接收机的替代结构
为了了解基本DCCN接收器中各层的贡献，我们通过替换和/或移除某些层来探索原始模型（a–g）的7种替代结构，如表V所列（–表示与原始层相同）。图13给出了用于16QAM的7个可选基本DCCN接收机的误码率性能。在8QAM中也发现了类似的结果，而所有的替代方案在BPSK和QPSK中的性能相同。除了c和d外，其他替代方案的性能几乎与原始的基本DCCN接收器相同。在方案a和方案g中，将原模型中类似DFT的C-Conv层替换为FC层，a和g达到与原DCCN相同的性能意味着FC层可以像C-Conv一样进行DFT转换层。在备选方案b和g中，移除R-Conv层，使得IQ数据和LRelu激活的IQ数据的组合被馈送到最后的解调FC层。它们表明R-Conv层对解调没有贡献。然而，R-Conv层可以加快训练速度。备选方案e表明，最后的LRelu活化可以用线性活化代替，而不会损害性能。在备选方案c和d中，移除R-Conv和跳过连接，以便IQ数据（c）或LRelu激活的IQ数据（d）被馈送到解调FC层。结果表明，对于较高的调制阶数，FC层不能仅基于IQ数据或非线性激活IQ数据进行解调。备选方案f也删除了跳过连接，但是，R-Conv层和2m滤波器在适当的地方挑选每个星座点。备选方案f表明，非线性激活的R-Conv层可以代替跳跃连接。

D. Cross Validation

In wireless communication, simulated channel model is often preferred over real channel in a limited environment since the former is considered more representative of environmental dynamics. Simulated channel model implemented by deep learning platforms, such as Tensorflow, brings training efficiency and convenience, especially with regards to back-propagation for autoencoders with both transmitter and receiver [6], [9]. However, in this paper, we found this practice may inflate the performance of trained model, which might be due to limited pseudo-random window of Tensorflow random generator, of which the random seeds could not be reset once flow graph is built. For example, in Fig. 14, our DCCN receivers without CP even outperform the Matlab benchmark, that tightly follows the theoretical limits. To avoid the risk of inflated performance, in [29], we provide a cross-validation platform, in which the received OFDM signal generated in Matlab is fed to the DCCN receiver implemented in Python, to get more trustable performance of our trained models

交叉验证
在无线通信中，由于模拟信道模型更能代表环境动力学，因此在有限的环境中，模拟信道模型往往比真实信道更具代表性。由深度学习平台（如Tensorflow）实现的模拟信道模型为训练带来了效率和方便，特别是对于同时具有发射机和接收机的自动编码器[6]，[9]。然而，在本文中，我们发现这种做法可能会提高训练模型的性能，这可能是由于张量流随机发生器的伪随机窗口有限，一旦建立流图，随机种子就无法重置。例如，在图14中，没有CP的DCCN接收机的性能甚至超过了严格遵循理论极限的Matlab基准测试。为了避免性能膨胀的风险，在[29]中，我们提供了一个交叉验证平台，将Matlab生成的OFDM信号输入到用Python实现的DCCN接收机中，以获得更可靠的训练模型性能

VI. CONCLUSION

In this paper, an OFDM receiver entirely based on Deep Complex Convolutional Networks (DCCN) is developed under the guidance of signal processing structures of expert OFDM receiver. Compared to existing works, the Deep Neuron Networks developed in this paper contains not just dense layers followed by non-linear activations, but also several new components: complex convolutional layers, residual blocks, and skip connections. Moreover, the developed model is mostly linear and only contains a few non-linear activations necessary for demodulation, therefore, it does not contradict with well-established signal processing techniques. On the other hand, several sophisticated training techniques are employed to improve the training efficiency, including the logarithmic biterror-rate in the loss function, exponential decay of learning rate, transfer learning for perpended module. Without using explicit (Inverse) Discrete Fourier Transformations, the DCCN receiver achieves performance that is comparable to expert OFDM receiver in AWGN channel, and outperforms it in lower to middle SNR regimes of Rayleigh channels. Moreover, the DCCN learns to exploit the cyclic prefix in OFDM symbol to enhance its performance in AWGN, flat and multi-path fading channels. However, the developed DCCN model still under-performs the expert receivers in high SNR regime and higher modulation orders. Furthermore, the DCCN model is fairly general: its hyper-parameters especially with alternative structures b and g, are basically independent from the modulation order.
This work demonstrates that Deep Learning is able to learn complex transformations in base-band signal processing,and therefore could learn (and potentially create) advanced waveforms in wireless communications. It also shows that Deep Learning could potentially improve the performance of wireless system in low SNRs. However, more work is required to achieve better performance in high SNR regime, as well as for higher order modulations, such as structures for learning higher-order interpolations

本文在专家OFDM接收机信号处理结构的指导下，开发了一种完全基于深复卷积网络（DCCN）的OFDM接收机。与已有的研究相比，本文提出的深部神经元网络不仅包含致密层，然后是非线性激活，还包含了几个新的组成部分：复数卷积层、残差块和跳跃连接。此外，所建立的模型大多是线性的，只包含一些解调所需的非线性激活，因此，它与成熟的信号处理技术并不矛盾。另一方面，为了提高训练效率，采用了一些先进的训练技术，包括损失函数中的对数误码率、学习率的指数衰减、独立模块的转移学习等。在AWGN信道中，DCCN接收机在不使用显式（逆）离散Fourier变换的情况下，获得了与专家OFDM接收机相当的性能，并且在Rayleigh信道的中低信噪比条件下优于专家OFDM接收机。此外，DCCN学习利用OFDM符号中的循环前缀来提高其在AWGN、平坦和多径衰落信道中的性能。然而，所建立的DCCN模型在高信噪比和更高的调制阶数下仍不能很好地满足专家接收机的要求。此外，DCCN模型是相当普遍的：它的超参数，特别是交替结构b和g，基本上与调制阶数无关。

这项工作表明，深度学习能够学习基带信号处理中的复数变换，因此可以学习（并可能创建）无线通信中的高级波形。研究还表明，在低信噪比下，深度学习有可能改善无线系统的性能。然而，为了在高信噪比下获得更好的性能，以及对于高阶调制，例如用于学习高阶插值的结构，还需要做更多的工作

ACKNOWLEDGMENT

This work is supported by US National Science Foundation grant NSF CNS 1731833.v

这项工作得到了美国国家科学基金会资助，NSF CNS 1731833.v