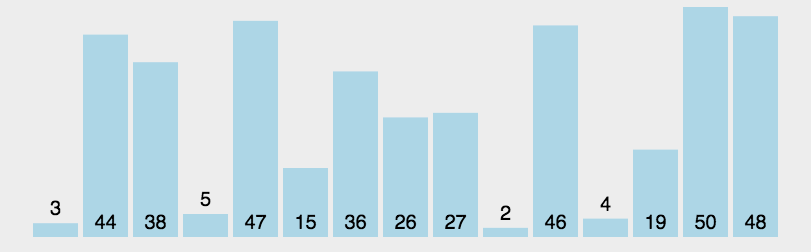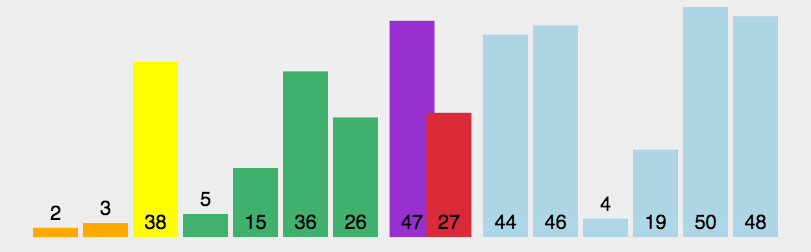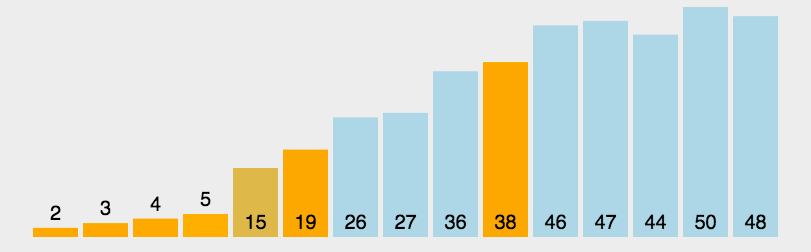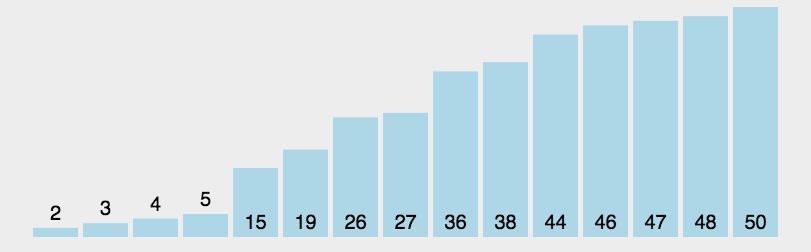
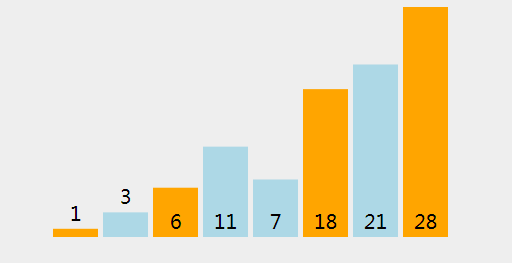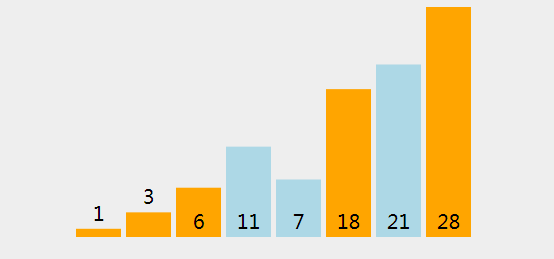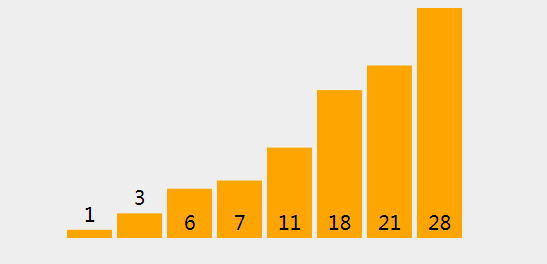【十大排序算法】(二)快速排序算法
一、基本思想
通过一趟排序将待排记录分隔成独立的两部分,其中一部分记录的关键字均比另一部分的关键字小,则可分别对这两部分记录继续进行排序,以达到整个序列有序。
二、算法分析
1、算法描述
快速排序使用分治法来把一个串(list)分为两个子串(sub-lists)。具体算法描述如下:
- 从数列中挑出一个元素,称为 “基准”(pivot);
- 重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面(相同的数可以到任一边)。在这个分区退出之后,该基准就处于数列的中间位置。这个称为分区(partition)操作;
- 递归地(recursive)把小于基准值元素的子数列和大于基准值元素的子数列排序。
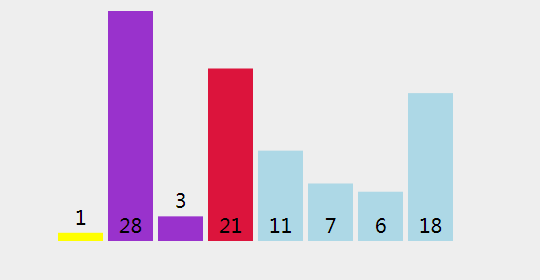
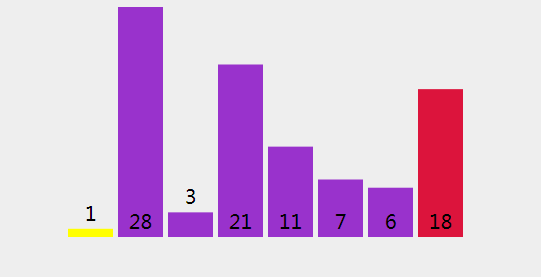
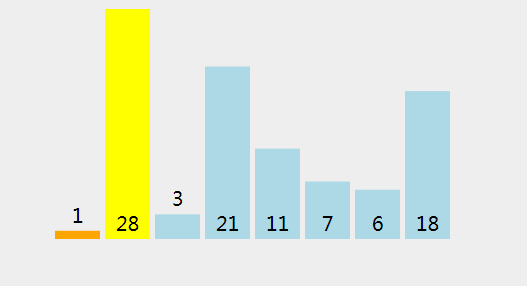
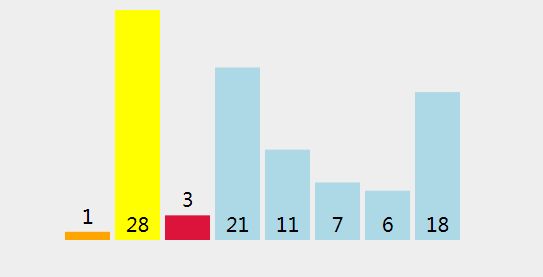
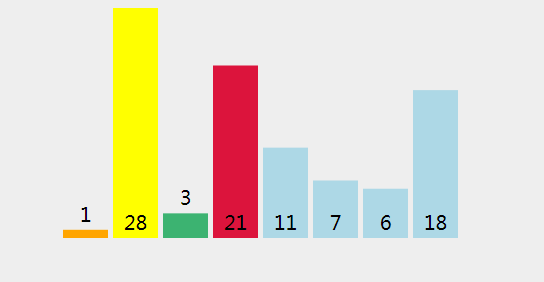
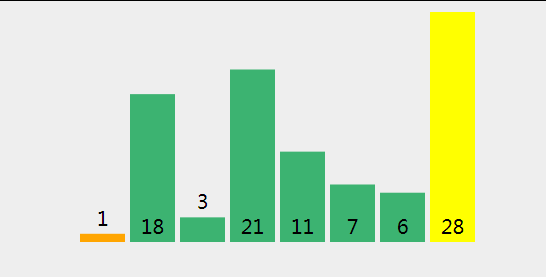
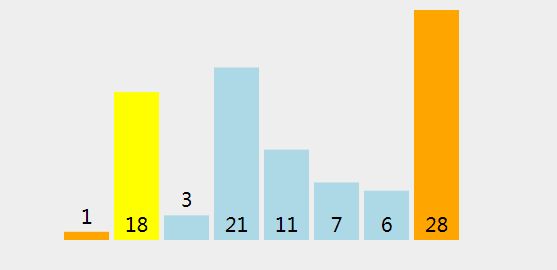
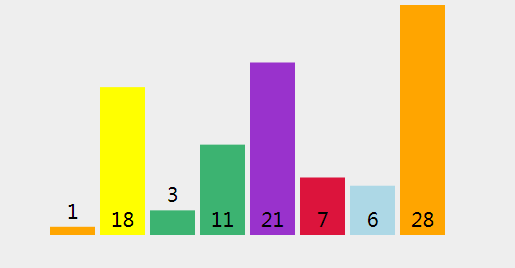
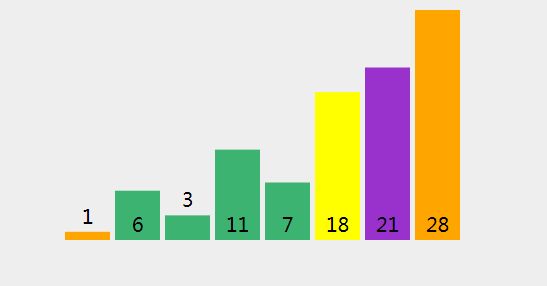
首先我们给定一个数组 int[] arr = {1,28,3,21,11,7,6,18};
下面我们来直观的描述下冒泡排序算法的过程:
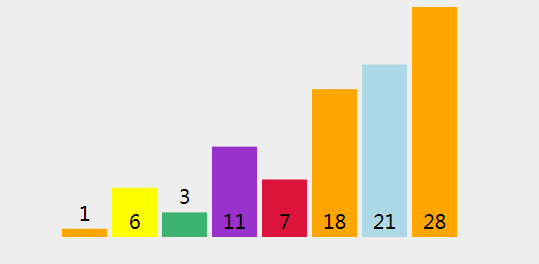
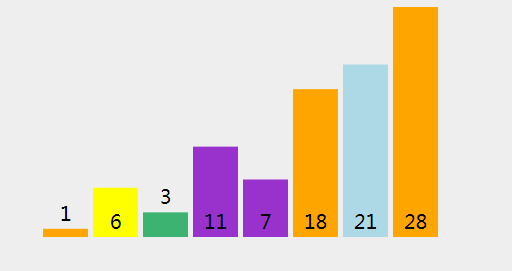
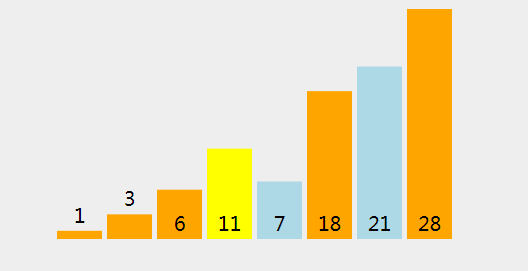
2、过程分析
(1)、检查是否 28 < 1 (轴心点).
(6)、遍历完成。
(8)、进行拆分 [28,3,21,11,7,6,18] (指数从 1 到 7 ,两边皆包括). 选择 28 作为轴心点. (存储指数 = 2.)
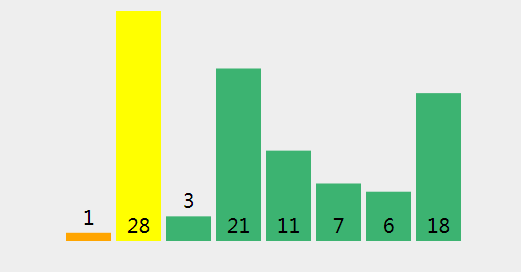
(13)、将轴心点(指数= 1, 值 = 28) 和在存储指数-1 的元素 (指数 = 7, 值 = 18) 进行交换)

(15)、进行拆分 [18,3,21,11,7,6] (指数从 1 到 6 ,两边皆包括). 选择 18 作为轴心点. (存储指数 = 2.)
(16)、检查是否 3 < 18 (轴心点).
(19)、11 < 18 (轴心点) 是真(True). 将指数为 4 (值 = {val}) 和在存储指数的元素 (指数 = 3, 值 = 21) 进行交换. (交换过后在存储指数上的值 = {4}).
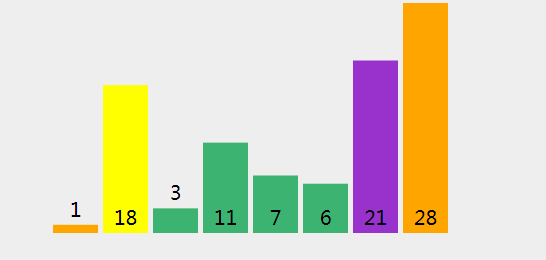
(22)、将轴心点(指数= 1, 值 = 18) 和在存储指数-1 的元素 (指数 = 5, 值 = 6) 进行交换)
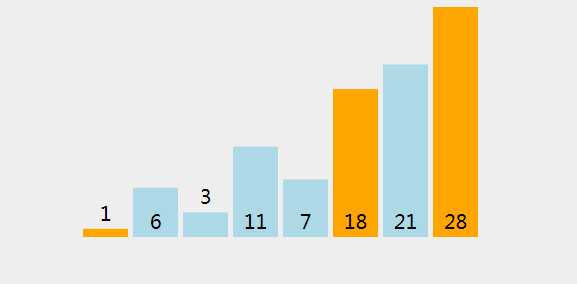
(24)、进行拆分 [6,3,11,7] (指数从 1 到 4 ,两边皆包括). 选择 6 作为轴心点. (存储指数 = 2.)
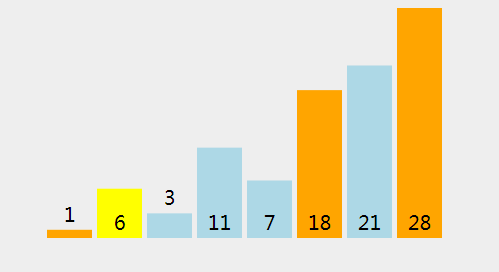
(25)、以此类推,检查是否 7 < 6 (轴心点).
(27)、将轴心点(指数= 1, 值 = 6) 和在存储指数-1 的元素 (指数 = 2, 值 = 3) 进行交换)
(28)、现在轴心点已经在排序过后的位置
(29)、进行拆分 [3] (指数从 1 到 1 ,两边皆包括). 因为拆分大小 == 1,在拆分项中的元素一定会在排序过后的位置。
(30)、进行拆分 [11,7] (指数从 3 到 4 ,两边皆包括). 选择 11 作为轴心点. (存储指数 = 4.)
(31)、检查是否 7 < 11 (轴心点).
(32)、遍历完成。
(33)、将轴心点(指数= 3, 值 = 11) 和在存储指数-1 的元素 (指数 = 4, 值 = 7) 进行交换)
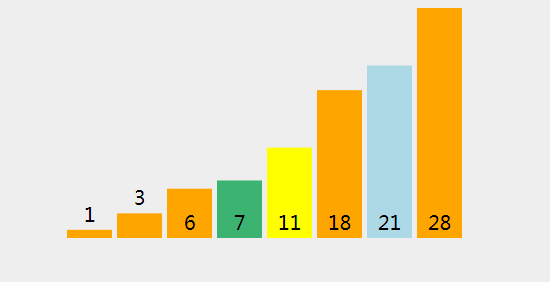
(34)、现在轴心点已经在排序过后的位置
(35)、进行拆分 [7] (指数从 3 到 3 ,两边皆包括). 因为拆分大小 == 1,在拆分项中的元素一定会在排序过后的位置。
(36)、进行拆分 [21] (指数从 6 到 6 ,两边皆包括). 因为拆分大小 == 1,在拆分项中的元素一定会在排序过后的位置。
3、动画演示
三、算法实现
package com.algorithm.tenSortingAlgorithm;
import java.util.Arrays;
public class QuickSort {
private static void quickSort(int[] arr, int low, int high) {
if (low < high) {
// 分区操作,将一个数组分成两个分区,返回分区界限索引
int index = partition(arr, low, high);
// 对左分区进行快排
quickSort(arr, low, index - 1);
// 对右分区进行快排
quickSort(arr, index + 1, high);
}
}
private static int partition(int[] arr, int low, int high) {
int pivot = arr[low];
while (low < high) {
// 1、先看右边,依次往左递减
while (pivot <= arr[high] && low < high) {
high--;
}
// 2、将右侧找到小于基准数的值加入到左边的(坑)位置, 左指针想中间移动一个位置
if (low < high) {
arr[low] = arr[high];
low++;
}
// 3、再看左边,依次往右递增
while (pivot > arr[low] && low < high) {
low++;
}
// 4、将左侧找到的打印等于基准值的值加入到右边的坑中,右指针向中间移动一个位置 high--
if (low < high) {
arr[high] = arr[low];
high--;
}
}
// 最后将基准为与low和high相等位置的数字交换
arr[low] = pivot;
// 返回基准值的位置索引
return low;
}
public static void main(String[] args) {
int[] arr = {1,28,3,21,11,7,6,18};
quickSort(arr, 0, arr.length - 1);
System.out.println(Arrays.toString(arr));
}
}
最佳情况:T(n) = O(nlogn)
最差情况:T(n) = O(n2)
平均情况:T(n) = O(nlogn)
四、十大排序算法总结
【十大排序算法】(一)冒泡排序算法
【十大排序算法】(一)冒泡排序算法(优化)
【十大排序算法】(二)快速排序算法
【十大排序算法】(三)选择排序算法
【十大排序算法】(四)堆排序算法
【十大排序算法】(五)插入排序算法
【十大排序算法】(六)希尔排序算法
【十大排序算法】(七)归并排序算法
【十大排序算法】(八)计数排序算法
【十大排序算法】(九)桶排序算法
【十大排序算法】(十)基数排序算法