一.学习红黑树前的准备:
- 熟悉基础数据结构
- 了解二叉树概念
二.红黑树的规则和规则分析:
- 根节点是黑色的
- 所有叶子节点(Null)是黑色的,一般会认定节点下空节点全部为黑色
- 如果节点为红色,那么子节点全部为黑色
- 从某一节点出发,到达叶子节点的所有分支上,黑色节点的数量相同
由规则4引出的一个定义,从根节点到叶子节点的黑色节点数量成为 树的黑色高度。我们会发现由于红色节点下全部为黑色节点,那么最极端的情况就是,根节点出发,左子树全部为黑色节点,右子树为红色-黑色轮换,这样设想下不难发现,树的最长路径<=最短路径 * 2,使树能够高度平衡,这也就代表着 查询红黑树 不会因为数据失衡 导致查询时间间隔相差巨大。另外,因为树到叶子的高度大致相等,这样根的值自然比较靠近于树的一个中位数。
红黑树 插入,删除,查询的最差的效率是 O(log n)
三.红黑树的插入操作
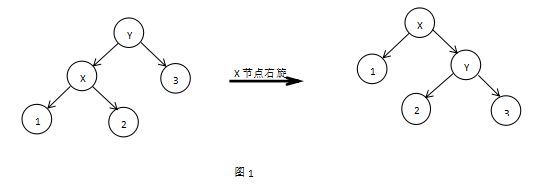
- 执行插入操作前,先完成两个操作,节点的左旋,右旋(旋转方法中不做颜色调整) (注意:在github中的代码方法 传入的参数 并非x 而是传入y作为参数)
节点左旋: 图中 x节点 , y节点 ,执行 x 的左旋右边的树,也就是 x 和 y 交换了位置,并且 x的左子节点 成了 y的 右子节点。

void leftRotate(Node x){ //满足条件才能进行左旋 assert y = x.parent == null || y.rightNode != x; x.parent = y.parent; y.parent = x; y.rightNode = x.leftNode; x.leftNode = y; }
节点右旋:右旋是左旋的逆向操作,如图所示,x节点,y节点,旋转后 x,y的位置交互,y的左子节点为x的右子节点。
void rightRotate(Node x){ //满足条件才能进行右旋 assert y = x.parent == null || y.leftNode != x; x.parent = y.parent; y.parent = x; y.leftNode = x.rightNode; x.leftNode = y; }
- 对于红黑树的插入操作,总体分为两步,1.执行插入,将插入的值放入相应的节点; 2.对插入的节点执行树的修复操作。(注意,对于新增的节点,默认节点是红色节点)
1.插入节点
这一步比较简单,基本上就是递归或者while循环都能解决,将传递的节点信息,按照vlaue大小比较,找到需要插入的位置,然后直接插入即可。
Node insertPosition(Node node ,int value){ Node newNode; if (value < node.value) { //小于放左边 if (node.leftNode == null) { newNode = new Node(); newNode.parentNode = node; newNode.value = value; node.leftNode = newNode; return newNode; } else { return insertPosition(node.leftNode, value); } } else { //大于等于放右边 if (node.rightNode == null) { newNode = new Node(); newNode.parentNode = node; newNode.value = value; node.rightNode = newNode; return newNode; } else { return insertPosition(node.rightNode, value); } } }
2.红黑树修复(下面N为待修复节点)
红黑树的修复总体能分为3种情况,1、修复的节点为根节点,2、修复的节点的父节点为黑色,3、修复的节点父节点为红色。
对于第一种情况,如果节点是根节点 ,那么将节点的颜色变更黑色。
对于第二种情况,如果父节点是黑色,那么直接结束修复,不做变更。
下面我们详细讨论第三种情况,即父节点为红色的情况。
1、父节点红色,叔父节点也为红色,进行如图所示变化,将父节点P和叔父节点U置为黑色,祖父节点G置为红色,然后祖父节点P代替 N节点 ,重新进行修复操作。
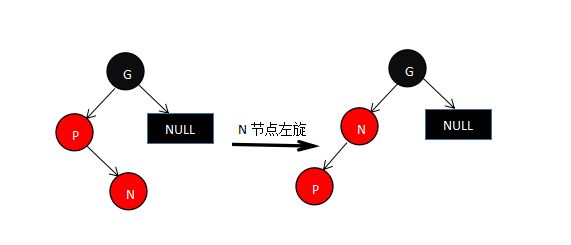
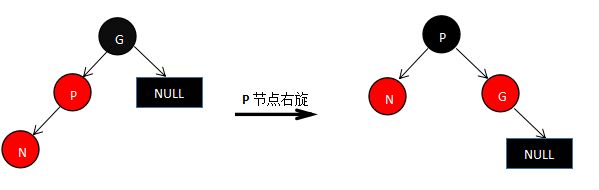
2、父节点为红色,叔节点为黑色 ,分为二种类型下四种情况,我们通过旋转,将类型进行转化。(一般这种情况,叔父节点均为黑色NUll叶子节点)
-
-
- 父节点和N节点在同一方向(1.同处于祖父节点的左边方向,2同处于祖父节点的右边方向)
- 父节点和N节点不在同一个方向(1.父节点在左,N节点在右 ,2.父节点在右,子节点在左),这种类型通过旋转,转化成第一种类型来进行修复
-
第二种类型:
如果是第二种类型,转变成第一种类型(如果父节点P在N节点的左边,执行N节点的左旋,父节点在N节点的右边,执行N节点的右旋),然后调用第一种类型的方法,但是调用方法时 节点变量应该传递父节点P
第一种类型:
如果方向为左,将父节点P右旋(方向为右,进行左旋),然后父节点P变为黑色,祖父节点G置为红色。
void repairNode(Node node) { //第一种情况 节点为根节点 if (node.parentNode == null) { node.color = Color.Black; return; } Node p = node.parentNode; //第二种情况 父节点为黑色 if (p.color == Color.Black) { return; } //第三种情况 父节点 为红色 if (p.color == Color.Red) { //获取node的叔父节点 Node u = getUncle(node); Color uncleColor = u == null ? Color.Black : u.color; Node g = getGrand(node); if (uncleColor == Color.Red) { //如果叔父节点也为红色 ,叔父节点和父节点全部置为黑色,祖父节点置为红色,然后继续执行祖父节点的修复 g.color = Color.Red; p.color = Color.Black; u.color = Color.Black; repairNode(g); }else{ //如果叔父节点 为黑色 //1.节点和父节点方向不同 if(g.leftNode == p && p.rightNode = node){ //父节点是左子节点,n节点在右子节点, 这时候 父节点 在 n 节点 的左边 执行 n节点的左旋 leftRotate(node); //将变量node 改为 node之前的父节点,进入第一种类型的修复 node = node.leftNode; }else if(g.rightNode == p && p.leftNode = node){ rightRotate(node); node = node.rightNode; } //经过之前的判断之后,这里就不做赘余的判断的 repairType1(node); } } } void repairType1(Node node){ Node p = node.parentNode; Node g = node.getGrand(node); p.color = Color.Black; g.color = Color.Red; if(p.leftNode == node){ rightRotate(p); }else{ leftRotate(p); } }
四.红黑树的删除操作
删除节点呢比插入操作更麻烦一点,不过基本上将情形梳理清楚即可。从总体上,删除节点可以分为以下几点(去除不可能发生的情况),
注:执行删除的节点为 节点N,节点N的子节点分为(左 SL, 右SR),如果图形中节点没有颜色,那么代表这个节点可能为红色或者黑色:
- 节点N有两个子节点
- 节点N只有一个子节点
- 节点N没有子节点
- 节点N有两个子节点,第一种情况下,将N替换,找出左子树中取最大值,或者右子树中的最小值 ,直接将节点N替换即可。
- 节点N只有一个子节点,对于这种情况,节点N的子节点S必定为红色,那么直接将子节点S进行旋转,子节点S占据节点N的位置,子节点S的颜色改为黑色,然后删除节点N即可。(SL进行右旋,SR进行左旋 )
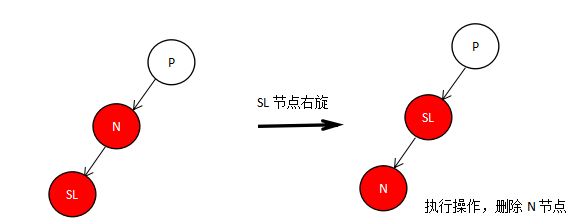
- 节点N没有子节点,这中情况下,如果N节点是红色,那么直接删除即可,我们主要考虑N节点为黑色的情况
3.1、N节点为红色(直接删除)
3.2、N节点为黑色(如果节点为黑色,那么兄弟节点必定不为空,否则路径上的黑色节点会多一个)
-
-
- N节点的兄弟节点为红色(转化为兄弟节点为黑色的情况)
将兄弟节点U旋转(U是左节点U右旋,右节点U左旋),并把P置为红色,U置为黑色,然后node再次执行3.2这个步骤,这时候会进入兄弟节点为黑色的情况
- N节点的兄弟节点为黑色
- N节点的兄弟节点U有红色子节点,判断红色子节点S方向是否与N节点的方向相反(相反的节点也就是离N最远的节点)
如果兄弟节点U的红色子节点S与N节点方向相同,那么进行 子节点S旋转(左节点右旋,右子节点左旋)并且和U交换颜色 ,转化到 方向相反的情况,如图: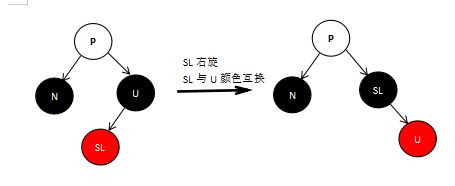
如果红色子节点S与N节点方向相反,兄弟节点U进行旋转,并且和P的颜色进行交换,然后将SR的颜色置为黑色,最后删除N节点即可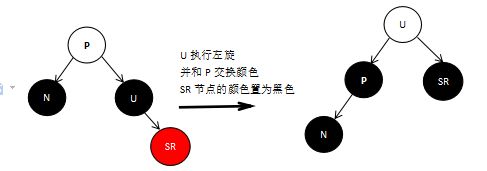
- N节点 兄弟节点U没有红色子节点(这种情况只能是 兄弟节点没有子节点)
判断父节点的颜色,如果父节点P颜色为红色,那么将父节点P的颜色置为黑色,兄弟节点U的颜色置为红色,然后删除N节点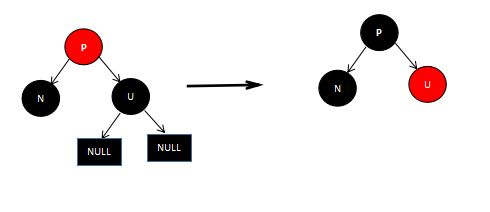
如果父节点P颜色为黑色,将兄弟节点U改为红色,删除N节点,然后以父节点P为参数重新执行 3.2 这个删除过程 进行树的修复,但是注意的是,修复时不再执行删除操作(因为这时候分支上少了一个黑色节点,而删除操作的流程会补充一个黑色节点,所以 以P节点为参数重新执行3.2过程,会自动补全少的黑色节点)。
- N节点的兄弟节点U有红色子节点,判断红色子节点S方向是否与N节点的方向相反(相反的节点也就是离N最远的节点)
- N节点的兄弟节点为红色(转化为兄弟节点为黑色的情况)
-
void deleteNode(Node node) { //1.判断node子节点数量 int sNum = (node.rightNode != null ? 1 : 0) + (node.leftNode != null ? 1 : 0); if (sNum == 2) { //情况1 如果有两个子节点 取左子树最大值 或者 右子树最小值的节点替换 Node maxNode = getNodeLeftMaxNode(node); //进行替换即可 node.value = maxNode.value; } if (sNum == 1) { //只有一个子节点 必定是节点为黑色,并且子节点为红色,直接用子节点替换该节点即可 Node newNode; if (node.leftNode != null) { newNode = node.leftNode; } else { newNode = node.rightNode; } newNode.parentNode = node.parentNode; if (node.parentNode.leftNode == node) { node.parentNode.rightNode = newNode; } else { node.parentNode.rightNode = newNode; } } if (sNum == 0) { if (node.color == Color.Red) { removeNode(node); } else { condition3_2(node, 1); } } } void condition3_2(Node node, int operator) { //operator 1 为执行删除 2.为进行修复 if (node.parentNode != null) { //这里brother必定不为null Node u = getBrother(node); Node p = node.parentNode; if (u.color == Color.Red) { p.color = Color.Red; u.color = Color.Black; if (p.leftNode == u) { rigthRotate(u); } else { leftRotate(u); } condition3_2(node, 1); } else { //检查兄弟节点下和node方向相反的子节点是不是红色 if (p.leftNode == node && getColor(u.rightNode) == Color.Red) { u.rightNode.color = Color.black; Color color = u.color; u.color = p.color; p.color = color; leftRotate(u); if(operator == 1){ removeNode(n); } return; }else if(p.rightNode == node && getColor(u.leftNode) == Color.Red){ u.rightNode.color = Color.black; Color color = u.color; u.color = p.color; p.color = color; rightRotate(u); if(operator == 1){ removeNode(n); } return; } //如果方向相反不是子节点,那么检查方向相同的子节点是不是红色 if(p.leftNode == node && getColor(u.leftNode) == Color.Red ){ Color color = u.color; u.color = u.leftNode.color; u.leftNode.color = u.color; rightRotate(u.leftNode); condition3_2(node,1); return; }else if(p.leftNode == node && getColor(u.leftNode) == Color.Red ){ Color color = u.color; u.color = u.leftNode.color; u.leftNode.color = u.color; leftRotate(u.leftNode); condition3_2(node,1); return; } //如果上面两种情况都不满足 ,说明兄弟节点没有红色子节点 if(p.color == Color.red){ p.color == Color.black; u.color = Color.red; if(operator == 1){ removeNode(node); } return; }else{ //这时候 只剩下父节点为黑色的情况 u.color = Color.red; if(operator == 1){ removeNode(node); } //执行修复 condition3_2(p,2); return; } } } else { if (operator == 1) { removeNode(node); } } } Color getColor(Node node) { return node == null ? Color.Black : node.color; }
以上就是红黑树的一些基础操作了,具体可以参考以前写的一个demo,不过为了方便,代码中旋转方法中传入的参数是 文中所说 N节点的父节点,所以需要注意这一点。仅供参考,如果不对,还请指正。
github路径: https://github.com/conquener/java-base/tree/master/src/main/com.hp.learn.base/redblacktree.