分门别类刷leetcode——难题
leetcode 315 计算右侧小于当前元素的个数——线段树+离散化
给定一个整数数组 nums,按要求返回一个新数组 counts。数组 counts 有该性质: counts[i] 的值是 nums[i] 右侧小于 nums[i] 的元素的数量。
示例:
输入: [5,2,6,1]
输出:[2,1,1,0]
解释:
5 的右侧有 2 个更小的元素 (2 和 1).
2 的右侧仅有 1 个更小的元素 (1).
6 的右侧有 1 个更小的元素 (1).
1 的右侧有 0 个更小的元素.思路:
思路与二叉查找树的类型(二叉查找树实现的思路及代码见:分门别类刷leetcode——二叉查找树)。利用线段树记录各个数字区间的数字个数。
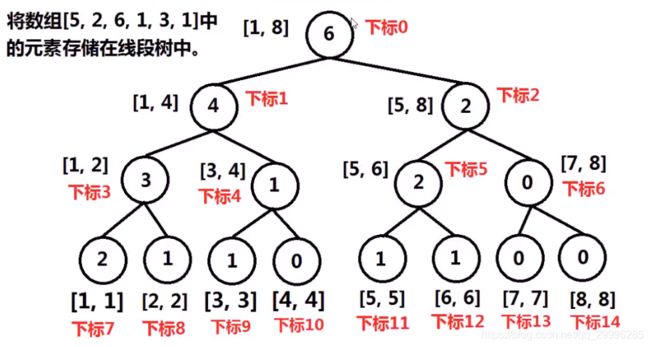
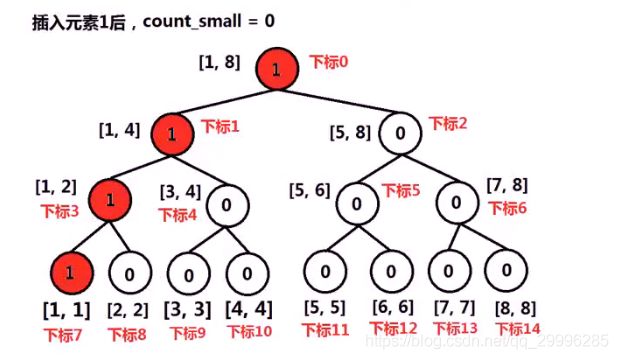
线段树是一颗完全二叉树,使用数组实现数据结构,线段树的根节点下标为0.
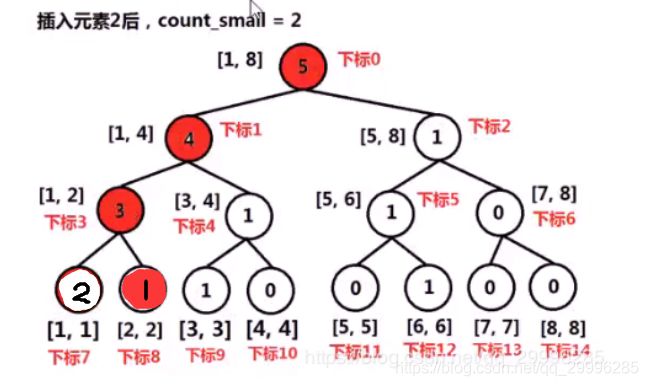
设某节点下标为 i ,则他左孩子下标为 2*i+1 , 右孩子下标为 2*i+2。线段树的节点中保存该节点对应区间范围内的数字个数。例如,区间[1, 4]中包含4个元素。
线段树的插入
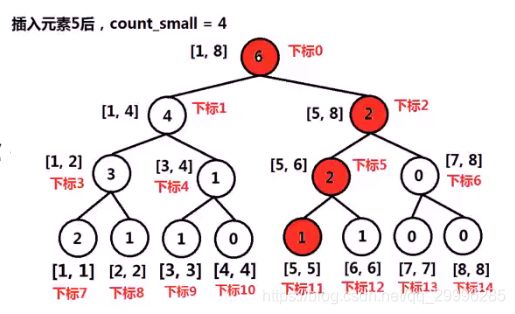
插入数据时,将元素按照原数组逆置后的顺序插入到线段树中,利用线段树表示的区间,记录在该区间中的数据个数。
递归的对数字进行插入,算法如下:
对于当前的线段树节点区间【left, right】的累加个数
- 如果当前未线段树的叶节点,则返回
- 计算区间的中段mid,将区间划分为【left, mid】和【mid+1, right】。计算左右孩子的下标。
- 如果num<=mid,递归的将num插入到节点的左区间中;
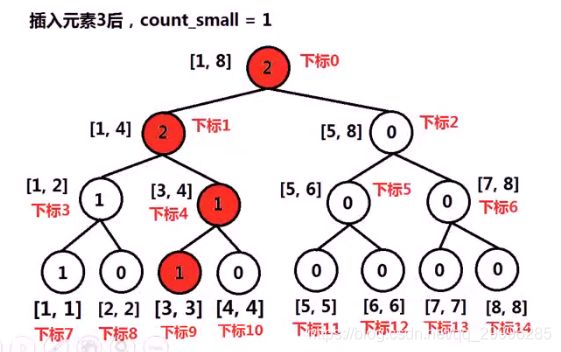
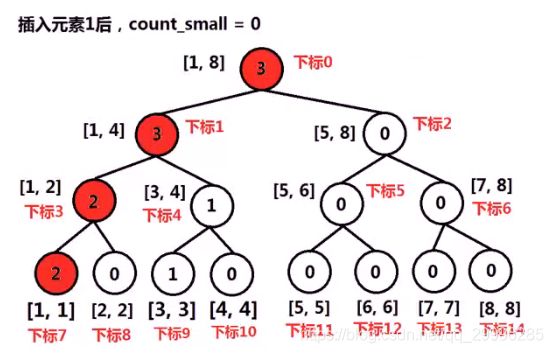
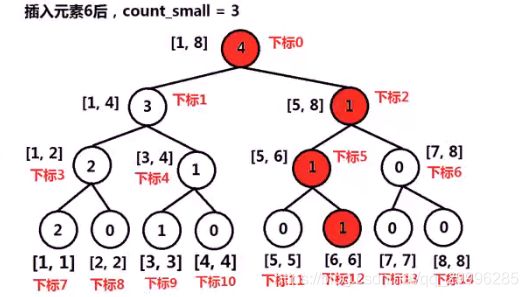
- 否则,使用count_small变量累加左区间的数据个数,递归的将num插入到该节点的右区间中。
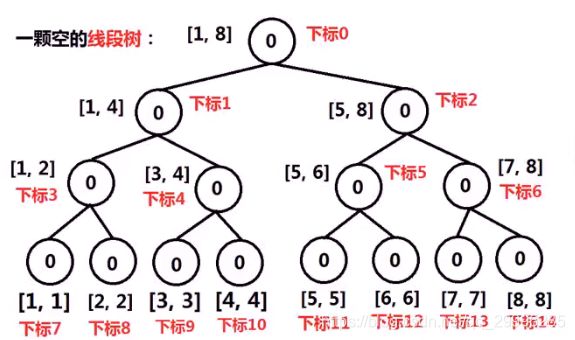
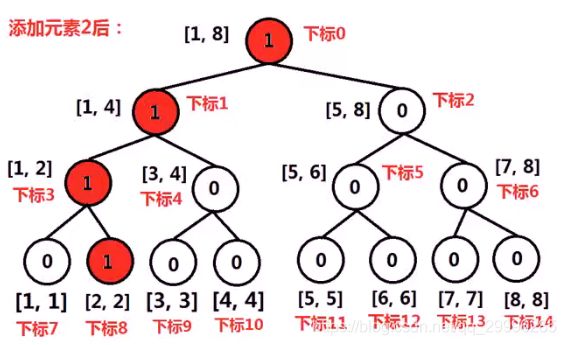
例如,将数组【5,2, 6,1,3,1】逆序后插入线段树的过程
实现代码:
void segment_tree_search(vector&tree, int num, int pos,
int left, int right, iint &count_small){
tree[pos]++;
//叶节点
if(left==right && num==left) return;
int mid=(left+right)/2;
int left_child=pos*2+1;
int right_child=pos*2+2;
if(num<=mid){
segment_tree_search(tree, num, left_child, left, mid, count_small);
}else{
count_small+=tree[left_child];
segment_tree_search(tree, num, right_child, mid+1, right, count_small);
}
} 但是,如果插入的数字之间的距离非常大,比如-9999999和+9999999.如果用线段树存储,则会耗费很大的空间,因此我们需要对输入的数据进行离散化。
离散化——一种不改变输入数据的大小,但是将数据的范围缩小的一种算法。
- 绑定,将源数字、新数字、源数字的围着绑定微一个结构体
- 按照源数字从小到大的顺序对结构体进行排序
- 离散化,按照排序后的顺序,从1开始设置源数字的离散化后的新数字
- 恢复顺序,按照原数字所在位置对结构体数字进行复原排序
struct discrete{
int num;
int dis_num;
int id;
discrete(int _num, int _dis_num, int _id):
num(_num),dis_num(_dis_num),id(_id){}
};
bool cmp1(const discrete &a, const discrete &b){
return a.num < b.num;
}
bool cmp2(const discrete &a, const discrete &b){
return a.id < b.id;
} void discrete_number(vector&nums, vector&dis_num){
vectortemp;
for(int i=0; i 整体实现代码:
struct discrete{
int num;
int dis_num;
int id;
discrete(int _num, int _dis_num, int _id):
num(_num),dis_num(_dis_num),id(_id){}
};
bool cmp1(const discrete &a, const discrete &b){
return a.num < b.num;
}
bool cmp2(const discrete &a, const discrete &b){
return a.id < b.id;
}
class Solution {
public:
void segment_tree_search(vector&tree, int num, int pos,
int left, int right, int &count_small){
tree[pos]++;
//叶节点
if(left==right && num==left) return;
int mid=(left+right)/2;
int left_child=pos*2+1;
int right_child=pos*2+2;
if(num<=mid){
segment_tree_search(tree, num, left_child, left, mid, count_small);
}else{
count_small+=tree[left_child];
segment_tree_search(tree, num, right_child, mid+1, right, count_small);
}
}
void discrete_number(vector&nums, vector&dis_num){
vectortemp;
for(int i=0; i countSmaller(vector& nums) {
vectortree;
vectorresult;
vectorcount;
vectordis_num;
if(nums.size()==0){
return result;
}
discrete_number(nums, dis_num);
for(int i=0; i<4*dis_num.size(); i++){
tree.push_back(0);
}
for(int i=dis_num.size()-1; i>=0; i--){
int count_small=0;
segment_tree_search(tree, dis_num[i], 0, 1, dis_num.size(), count_small);
count.push_back(count_small);
}
for(int i=count.size()-1; i>=0; i--){
result.push_back(count[i]);
}
return result;
}
}; 本题的另外两种解法见:分门别类刷leetcode——二叉查找树 和 分门别类刷leetcode——二分查找与分治算法
leetcode 224 基本计算器——秋招有公司考过,我忘了是哪个公司了
实现一个基本的计算器来计算一个简单的字符串表达式的值。
字符串表达式可以包含左括号 ( ,右括号 ),加号 + ,减号 -,非负整数和空格 。
示例 1:
输入: "1 + 1"
输出: 2
示例 2:
输入: " 2-1 + 2 "
输出: 3示例 3:
输入: "(1+(4+5+2)-3)+(6+8)"
输出: 23说明:
- 你可以假设所给定的表达式都是有效的。
- 请不要使用内置的库函数
eval。
思路:
利用栈,把表达式拆分
使用数字栈存储数组,操作符栈表示操作符(不包括括号)
算法设计:
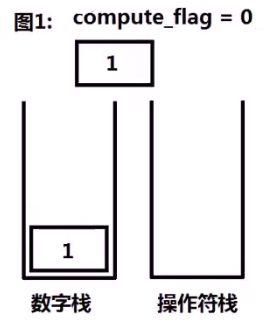
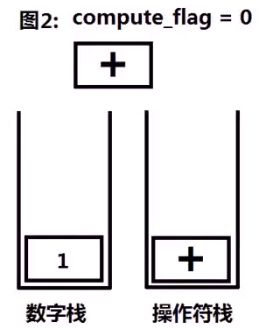
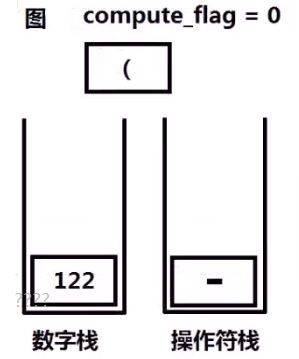
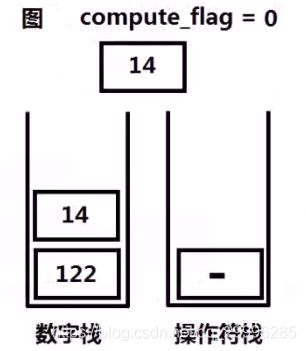
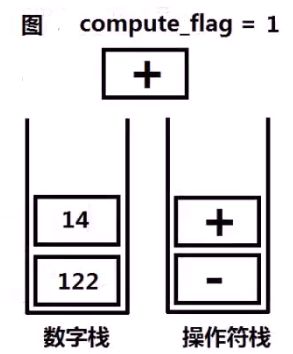
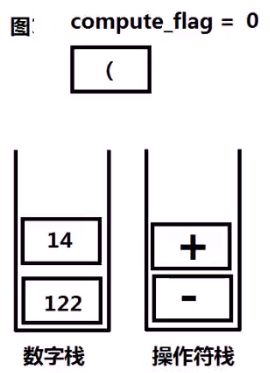
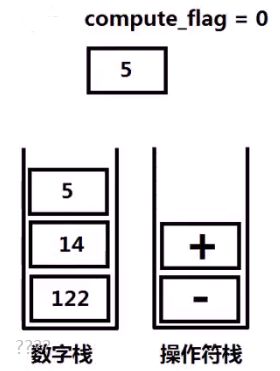
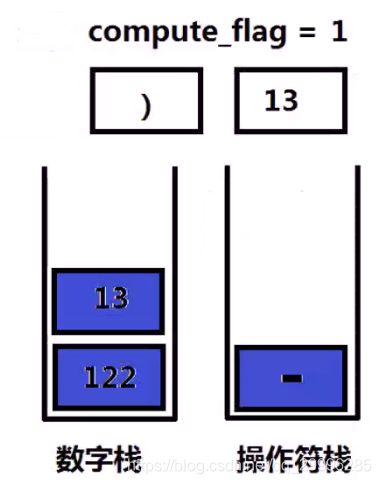
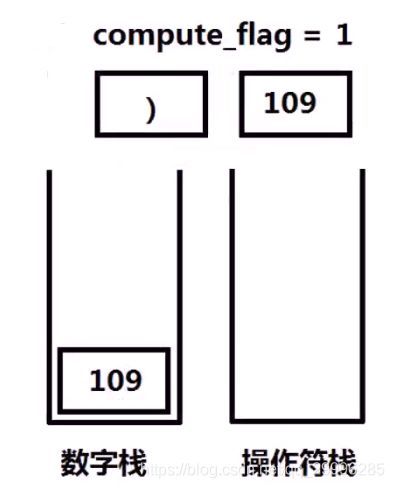
1、设置一个变量compute_flag=0用以标记是否进行计算,(0时不进行计算,1时进行计算)与两个栈,数字栈和操作符栈。
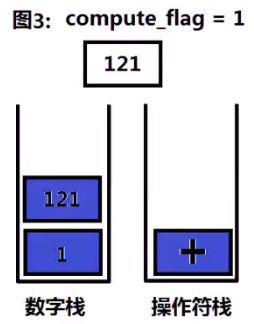
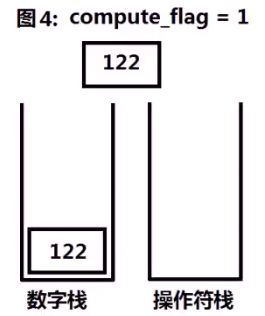
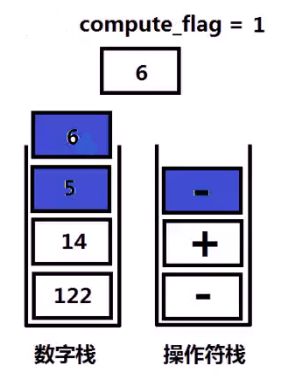
2、如果遇到操作数,且此时compute_flag=0,则数字入栈,否则,操作数入栈后进行计算。
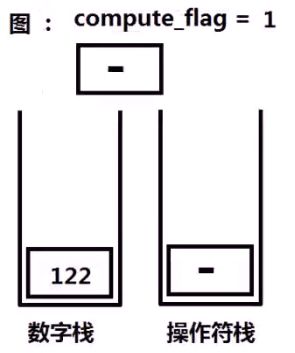
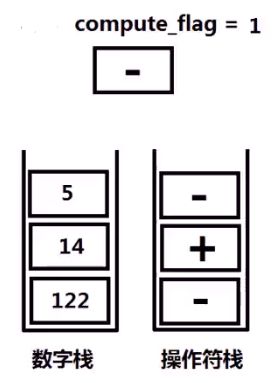
3、如果遇到操作符:
- 若操作符为 + - ,操作符入栈,compute_flag=1;
- 若操作符为 ( ,compute_flag=0
- 若操作符为 ),在进行计算。
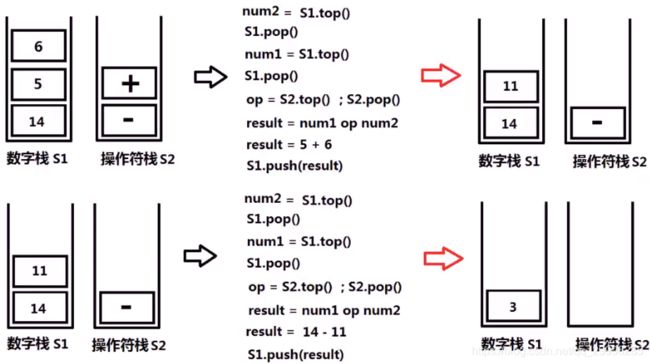
例如:
对于字符串处理:
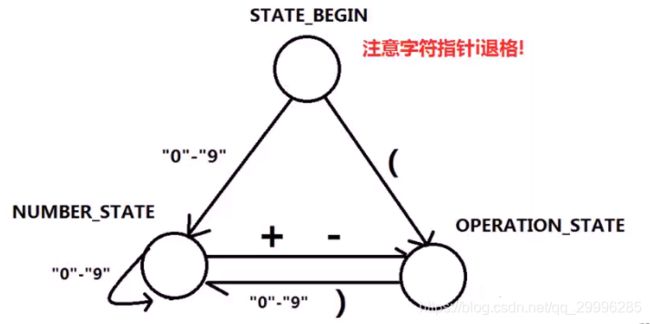
使用有限状态自动机(分门别类刷leetcode——贪心算法里面的leetcode 376也使用了自动机来解决)。
状态用圆圈表示,状态转换用箭头表示。
- 在state_begin状态时,下一个字符可能是数字,也可能是 ( 。如果遇到是在则转为number_state,遇到 ( 则转为operation_state状态。
- 在number_state状态,如果遇到数字则状态不变,如果遇到 + -,则转为operation_state
- 在operation_state状态时,如果遇到数字则转化为number_state状态
由此可得用于计算的函数compute:
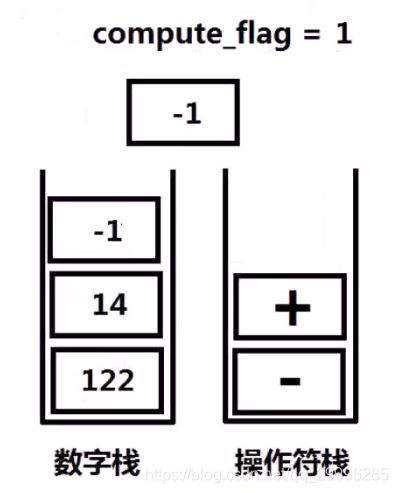
void compute(stack&number_stack, stack&operation_stack){
//数字栈的容量小于2
if(number_stack.size()<2) return;
//从数字栈中取出两个数字
int num2=number_stack.top();
number_stack.pop();
int num1=number_stack.top();
number_stack.pop();
if(operation_stack.top()=='+'){
number_stack.push(num1+num2);
}
else if(operation_stack.top()=='-'){
number_stack.push(num1-num2);
}
operation_stack.pop();
} 整体实现代码:
class Solution {
public:
void compute(stack&number_stack, stack&operation_stack){
//数字栈的容量小于2
if(number_stack.size()<2) return;
//从数字栈中取出两个数字
int num2=number_stack.top();
number_stack.pop();
int num1=number_stack.top();
number_stack.pop();
if(operation_stack.top()=='+'){
number_stack.push(num1+num2);
}
else if(operation_stack.top()=='-'){
number_stack.push(num1-num2);
}
operation_stack.pop();
}
int calculate(string s) {
static const int STATE_BEGIN=0;
static const int NUMBER_STATE=1;
static const int OPERATION_STATE=2;
stacknumber_stack;
stackoperation_stack;
int number=0;
int STATE=STATE_BEGIN;
int compuate_flag=0;
for(int i=0; i='0' &&s[i]<='9'){
STATE=NUMBER_STATE;
}else{
STATE=OPERATION_STATE;
}
//每次状态转换时,都需要做一次退格
i--;
break;
case NUMBER_STATE:
if(s[i]>='0' &&s[i]<='9'){
number=number*10+s[i]-'0';
}else{
number_stack.push(number);
if(compuate_flag==1){
compute(number_stack, operation_stack);
}
number=0;
i--;
STATE=OPERATION_STATE;
}
break;
case OPERATION_STATE:
if(s[i]=='+' || s[i]=='-'){
operation_stack.push(s[i]);
compuate_flag=1;
}else if(s[i]=='('){
STATE=NUMBER_STATE;
compuate_flag=0;
}else if(s[i]>='0' &&s[i]<='9'){
STATE=NUMBER_STATE;
i--;
}else if(s[i]==')'){
compute(number_stack, operation_stack);
}
break;
}
}
if(number !=0){
number_stack.push(number);
compute(number_stack, operation_stack);
}
if(number ==0 && number_stack.empty()){
return 0;
}
return number_stack.top();
}
};