CNN网络详细讲解,可视化图例解读
写在前面
想了解CNN详细网络工作过程的,可以直接找到第二部分,如果大家觉得有什么不对的地方,非常感谢留言指教~感激不尽
1. CNN网络应用场景
- 对二维图像进行特征提取。可以和多种网络进行拼接,比如可以在一个网络的前端使用CNN网络,然后再网络的后半部分接入其他的网络来共同实现较为复杂的功能
2. CNN的详细网络构成
2.1 CNN网络总览(VGG-16为例)
2.2 CNN网络内部所有参数(VGG-16为例)
2.3 CNN网络内部结构分析(VGG-16为例)
- 原图:大小尺寸为224×224×3(这里的3指的是RGB三个通道)
- 1~2层(灰色):卷积层,每一层有64个尺寸都是3×3的卷积核,所以原图做一次卷积之后得到的图的个数为64个不同的特征图,尺寸都是224×224,这就是“224×224×64”的来源。
【可能出现的疑问】:
//上面提到:卷积核的尺寸是3×3,权重的个数中的(3×3×3)×64中的 “3×3×3” 是怎么来的呢?//
答:由于是RGB三个通道,所以一共有3×3×3个参数,再加上有64个这样的卷积核,所以最后生成的参数为(3×3×3)×64。
//为什么做完卷积之后的特征图尺寸依然和原图一样都224×224呢,按照常理应该变小呀。难道不应该按照卷积的运算规律:卷积后的特征图尺寸=原图大小-卷积核尺寸+1变成 224-3+1=222么?//
答:按照常理来说,CNN在做卷积的时候会将边缘的那一圈的信息忽略,表现为特征图随着层数的加深而变小。但是,这里采用了padding的方式将边缘的损失给补偿了,大家可以去了解一下什么是CNN卷积过程中的padding方法(可以参考https://blog.csdn.net/program_developer/article/details/80369565)。总之,经过padding之后,卷积过后的原图就不会变小了~~,也就是保持卷积之前的原图和卷积之后的图(在进入池化层之前)是一样大的
//为什么在第一个卷积层中,权重个数为(3×3×3)×64,而第二个卷积层中,权重的个数为(3×3×64)×64,而第三个卷积层中,权重的个数变成了(3×3×64)×128?//
这也就解释了,为什么每一层的“权重参数(weight)”总是:
3 × 3 × 上 一 层 输 出 图 的 厚 度 ( 上 一 层 卷 积 核 的 数 量 ) × 本 层 使 用 卷 积 核 的 数 量 3 × 3 ×上一层输出图的厚度(上一层卷积核的数量)× 本层使用卷积核的数量 3×3×上一层输出图的厚度(上一层卷积核的数量)×本层使用卷积核的数量。
-
第3层(红色):池化层,这里采用的池化方法为最大池化。其目的是为了将参数的量进行大规模的缩小、简化,去掉很多重复、冗余的信息。经过池化层过后,特征图的尺寸缩小了1/4(长宽各减少一半)
-
第4-5层(灰色):卷积层,和1-2层一样,只是尺寸与池化层的一致,但是卷积核数目增多为128个,在前面1-2层64个卷积核提取的特征图的基础上再进行更高(深)维度特征的提取,最后得到128个特征图。
【可能疑问】:
// 这个过程到底产生多少个特征图呢?//
答:其实在每一个卷积层结束的时候,这个卷积层所使用的所有 的卷积核,无论是64个还是128个,最后产生的所有特征图叠加在一起,形成一张很厚的(通道数很多的)特征图,看作一个整体作为下一层的输入。
比如,原图在第1层用了64个不同的卷积核,提取了64个特征,产生的64个不同的特征图叠加到一起变成了一个通道为 64 的特征图,这64个特征图每一个的厚度都是1(通道数都是1,因为虽然再卷积的时候卷积核与RGB三个通道都进行运算,但是最终得到特征图的时候把RGB三个通道的数据叠加在一起了作为一个整体的特征图,所以说每个特征图的通道数为1)。
然后再把这64张图作为一个厚厚的整体(厚度为64)输入第二层,作为第二层的“原图”,再用64个不同的、厚度为64的3×3的卷积核进行【立体卷积】提取到64个不同的特征图(厚度为1)特征图,然后你就可以把这64张厚度为1的特征图,再看成厚度为64的一张特征图。然后再进行池化操作削减参数规模,随后后在进入第4层,虽然第4层卷积核个数变成了128个,那也是在前面特征图叠加完的最终特征图上,再提取128个更深层次的特征。原理还是一样,采用【立体卷积的思想】
【立体卷积】
只要厚度(通道数一致),进行卷积运算,最后得到的特征图永远都是厚度为1。比如:
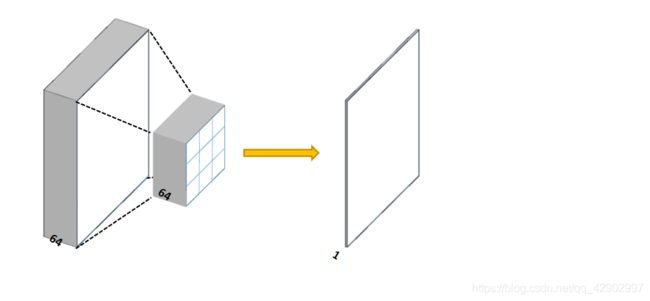
这样的话,是不是容易理解了好多~
【其实只要记住】:
① 只要卷积核的厚度何被卷积的图一致,卷出来的特征图永远都是厚度为1。
② 有多少个不同的卷积核,最后得到的特征图就有多少张。
- 第6层:依然最大池化层
- 第7-9层:依然卷积层,只不过深度再次增加,提取更高维度的特征信息
- 第10-18层:依然重复上面的活动
- 第19-20层:全连接层,从第18层,也就是最后一层池化层出来的特征图已经是高度抽象并且具有非常精炼的特征。在全连接层所进行的工作,就是把一副二维的特征图平铺展开为一个一维的数组,然后进行softmax操作就可以得到相应的类别。
========================================================
下面演示的过程中,为了方便观看,在分析最后一个池化层的时候,不使用7×7×512的尺寸,使用4×4×512的尺寸,因为画图更加方便一些。同样地,全连接层也不使用1×1×4096,转而使用1×1×15,Softmax层也不使用1×1×1000,转而使用1×1×10。
【可能的问题】:
//最后的池化层出来的数据代表什么?他是如何进入全连接层的?//
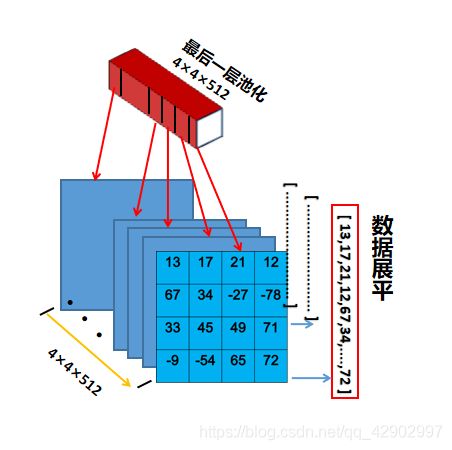
答:假设下图是一个最后池化层出来的512张4×4特征图其中的一张:
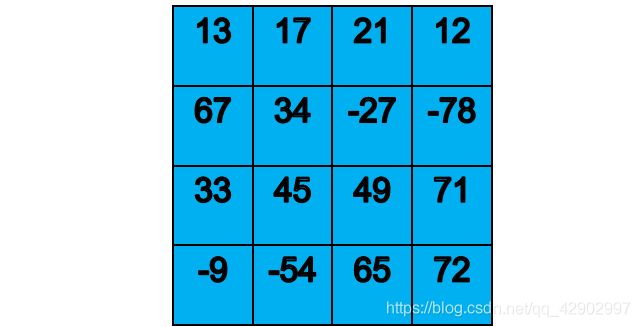
那么,这个特征图就代表了你前面所有过程中提取到的所有的信息的一部分(也就是说,最后一个池化层的厚度512,代表512张特征图,这些所有的图代表了整个原图的全部细节特征)。
然后,在进入全连接层之前,每一张4×4的二维特征图要展开成为一组列向量:[13,17,21,12,67,34,…,72],然后进入全连接层,如下图:
//最后一个池化层的数据维度(16×1)如何与全连接层的隐藏层(15×1)匹配呢?而全连接层内部又是如何进行工作最后输出分类结果的呢?//
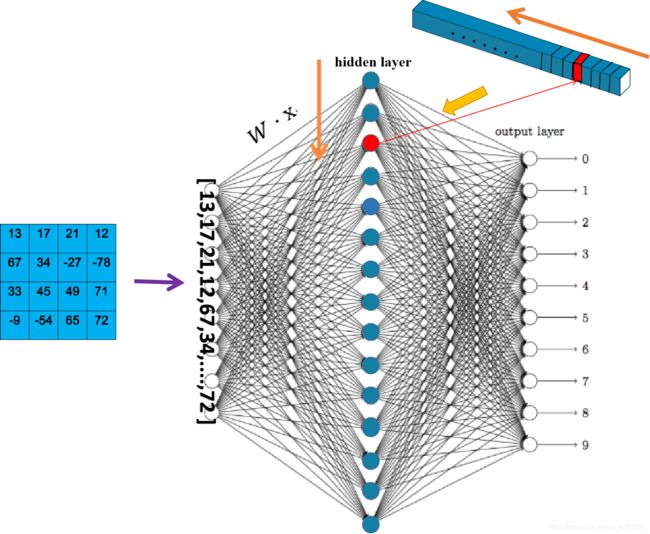
答:其实,只需要将最后一层池化展开的 “16行1列” 的数据与相应的权重矩阵相乘,就可以完成匹配这个步骤。见下图,其中 W 就是权重矩阵:
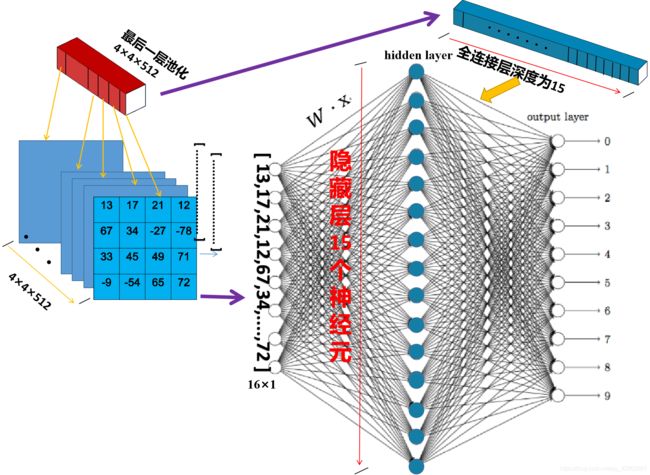
图中可以看的很清楚,“16×1”的矩阵为 x(共有16x的值,x1·····x16)作为input layer,权重矩阵为W,W·x 之后将送入hidden layer。
x 的每一个数据(x1·····x16)可以看作一个神经元节点。
所以 W·x 要符合下一层神经层(hidden layer)的输入,得到一个“15×1”的数据,W 矩阵的尺寸就要为“15×16”。如此以来就可以实现 15×16 × 16×1 = 15×1的目的。
然后,当数据在hidden layer中进行计算的时候,经过神经元中的 “激活函数” 之后,相应的隐藏层神经元数据满足了“激活”的条件,被“点亮”激活,就相当于“匹配到了特定的特征”,最后将所有“点亮”的神经元的数据进行汇总作为神经网络分类的依据。例如:
图中专门拿出了一张特征图(最后一个池化层输出的512个的其中一个)。输入最后的全连接层之后,可以看到在hidden layer中“点亮”了一个神经元。“点亮”的概念是,特征图在经过矩阵运算和激活函数处理之后,得到的那个最大的概率值作为“被点亮”的神经元节点。
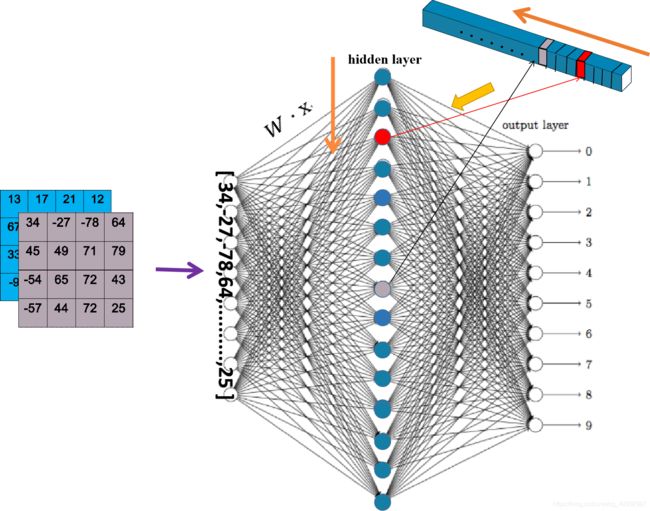
在上一张特征图的基础上,上图中再示范一张特征图(也是512张其中的一张),展示了两张特征图对 hidden layer 的神经元的总和激活情况。
可以看到,又有一个神经元被点亮了。
所以,当512张图全部输入进去的话,每一个特征图经过矩阵的运算和激活函数都会“点亮”隐藏层的一个神经元节点,也就是说所有的特征图可以点亮很多的神经元节点,而这些隐藏层的节点坦白地讲就是每一个神经元代表一个概率值(0~1之间)然后,这些所有的隐藏层的神经元所代表的数据会作为“输出层”的输入数据,再次进行矩阵运算和激活函数,最终输出一个最大的概率值,作为最终的 output 结果。
可以看到图中的Softmax层,绿色的代表被点亮的神经元,所以第2类被判断为最终的输出结果。