冒泡排序、选择排序、快速排序和归并排序（图解+代码）

一、排序的基本概念

1、排序

假设含n个记录的序列为{ R₁, R₂, …， R_n }其相应的关键字序列为 { K₁,K₂, …，K_n }。经过排序确定一种排列{ R_p1≤R_p2≤…≤R_pn}，使得它们的关键码满足如下递增或递减的关系 K_p1≤ K_p2 ≤…≤ K_pn 或 K_p1≤ K_p2 ≤…≤ K_pn 。

2、稳定排序和不稳定排序

• 对于任意的数据元素序列，若排序前后所有相同关键字的相对位置都不变，则称该排序方法称为稳定的排序方法。
• 若存在一组数据序列，在排序前后，相同关键字的相对位置发生了变化，则称该排序方法称为不稳定的排序方法。
• 例如，对于关键字序列3，2，3，4，若某种排序方法排序后
  变为2，3，3，4，则该排序方法是不稳定的。

3、 内部排序和外部排序

内部排序：指代排序记录全部存放在内存中进行排序的过程。
外部排序：指待排序的记录数量很大，以至于内存不能容纳全部全部记录，在排序过程中需要对外存进行访问的排序过程。

4、进行排序的两种基本操作

（1）比较两个关键码的大小
（2）将记录从一个位置移到另一个位置

二、直接插入排序

1、排序过程

整个排序过程为n-1趟插入，即先将序列中第1个记录看成是一个有序子序列，然后从第2个记录开始，逐个进行插入，直至整个序列有序。

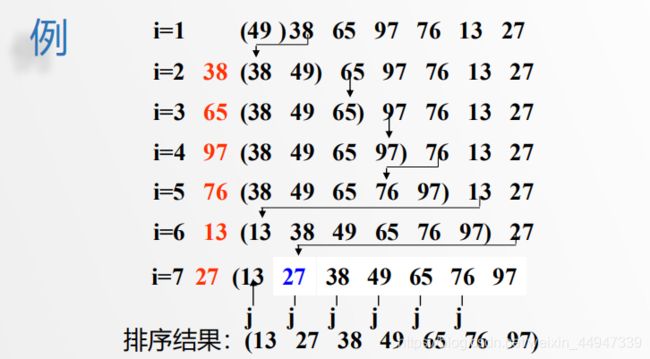
2、图解

3、【函数】用直接插入排序对整数序列进行非递减排序

void insertSort(int data[], int n)
//将data[0] - data[n-1]的n个整数按非递减有有序的方式进行排列
{
	int i, j;
	int temp;
	for (i = 1; i < n; i++) {	
		if (data[i] < data[i - 1]) {
			temp = data[i];
			data[i] = data[i - 1];
			for (j = i - 2; j >= 0 && data[i] > temp; j--) {
				data[j + 1] = data[j];
				data[j + 1] = temp;
			}
		}
	
	}
}

4、算法评价

时间复杂度：T(n)=O(n²)
空间复杂度：S(n)=O(1)

若待排序记录按关键字从小到大排列(正序)
关键字比较次数：n-1
记录移动次数：2(n-1)

若待排序记录按关键字从大到小排列(逆序)
关键字比较次数：(n+2)(n-1)/2
记录移动次数：(n+4)(n-1)/2

若待排序记录是随机的，取平均值
关键字比较次数：n²/4
记录移动次数：n²/4

三、冒泡排序

1、排序过程

（1）将第一个记录的关键字与第二个记录的关键字进行比较，若为逆序 r[1].key > r[2].key ，则交换；然后比较第二个记录与第三个记录；依次类推，直至第n-1个记录和第n个记录比较为止——第一趟冒泡排序，结果关键字最大的记录被安置在最后一个记录上
（2）对前n-1个记录进行第二趟冒泡排序，结果使关键字次大的记录被安置在第n-1个记录位置
（3）重复上述过程，直到“在一趟排序过程中没有进行过交换记录的操作”为止

2、图解：

3、【函数】用冒泡排序对整数序列进行非递减排序

void bubbleSort(int data[], int n)
//将data[0] - data[n-1]的n个整数按非递减有有序的方式进行排列
{
	int i, j, tag = 1;	//用tag表示排序过程中是否交换过元素值
	int temp;
	for (i = 1; tag&&i < n; i++) {	//i用于计算躺输，最多n-1趟
		tag = 0;
		for (j = 0; j < n - i; j++) {
			temp = data[j];
			data[j] = data[j + 1];
			data[j + 1] = temp;
			tag = 1;
		}
	}
}

4、算法评价

时间复杂度：T(n)=O(n²)
空间复杂度：S(n)=O(1)

最好情况（正序）
比较次数：n-1
移动次数：0

最坏情况（逆序）
比较次数：1/2(n²-n)
移动次数：3/2(n²-n)

冒泡排序是一种稳定的排序方法。

四、简单选择排序

1、排序过程

（1）首先通过n-1次关键字比较，从n个记录中找出关键字最小的记录，将它与第一个记录交换
（2）再通过n-2次比较，从剩余的n-1个记录中找出关键字次小的记录，将它与第二个记录交换
（3）重复上述操作，共进行n-1趟排序后，排序结束

2、图解

3、【函数】用简单选择排序对整数序列进行非递减排序

void selectSort(int data[], int n)
//将data[0] - data[n-1]的n个整数按非递减有有序的方式进行排列
{
	int i,j,k;
	int temp;
	for (i = 0; i < n-1; i++) {	
		k = i;
		for (j = i + 1; j < n; j++)	//找出最小元素的下标
			if (data[j] < data[k])
				k = j;
		if (k != j) {
			temp = data[i];
			data[i] = data[k];
			data[k] = temp;
		}
	}
}

4、算法评价

时间复杂度：T(n)=O(n²)
空间复杂度：S(n)=O(1)

记录移动次数
最好情况：0
最坏情况：3(n-1)
比较次数：n(n-1)/2

五、快速排序

1、基本思想

通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列

2、排序过程

• 对r[s……t]中记录进行一趟快速排序，附设两个指针i和j，设划分元记录rp=r[s]，x=rp.key
• 初始时令i=s,j=t
• 首先从j所指位置向前搜索第一个关键字小于x 的记录，并和rp交换
• 再从i所指位置起向后搜索，找到第一个关键字大于x的记录，和rp交换
• 重复上述两步，直至i==j为止
• 再分别对两个子序列进行快速排序，直到每个子序列只含有一个记录为止

3、图解

4、【函数】快速排序过程中的划分

int partition(int data[], int low, int high)
//用data[low]的值作为枢轴元素pivot进行划分
//使得data[low…i-1]均不大于pivot，data[i+1…high]均不小于pivot
{
	int i, j;
	int pivot;
	pivot = data[low];
	i = low;
	j = high;
	while (i < j) {				//从数组的两端交替地向中间扫描
		while (i < j&&data[j] >= pivot)j--;
		data[i] = data[j];		//比枢轴元素小者向前移
		while (i < j&&data[i] <= pivot)i++;
		data[j] = data[i];		//比枢轴元素大者向后移
	}
	data[i] = pivot;
	return i;		//返回枢轴元素的位置
}

5、【函数】用快速排序方法对整型数组进行非递减排序

void quickSort(int data[], int low,int high)
//用快速排序方法对整型数组进行非递减排序
{
	if (low < high) {
		int loc = partition(data, low, high);	//进行划分
		quicksort(data, low, i - 1);		//对前半区进行快速排序
		quicksort(data, i + 1, high);		//对后半区进行快速排序
	}
}

6、算法评价

时间复杂度

• 最好情况（每次总是选到中间值作划分元）
  T(n)=O(nlog2n)
• 最坏情况（每次总是选到最小或最大元素作划分元）
  T(n)=O(n²)

空间复杂度：需栈空间以实现递归

• 最坏情况：S(n)=O(n)
• 一般情况：S(n)=O(log2n)

六、归并排序

1、归并排序

归并——将两个或两个以上的有序表组合成一个新的有序表，叫归并排序。

2、路归并排序

排序过程：设初始序列含有n个记录，则可看成n个有序的子序列，每个子序列长度为1两两合并，得到 n/2 个长度为2或1的有序子序列再两两合并，……如此重复，直至得到一个长度为n的有序序列为止。

3、图解

4、【函数】将分别有序地data[low…mid-1]和ddata[mid…high] 归并为有序的data[low…high]

void merge(int data[], int low, int mid, int high)
//将有序子序列data[low…mid-1]和data[mid…high]归并为有序序列data[low…high】
{
	int i,p , k;
	int *tmp;
	tmp =(int*)malloc((high - low + 1) * sizeof(int));
	if (!tmp)
		exit(0);
	k = 0;
	for (i = low, p = mid; i < mid &&p <= high;)
		if (data[i] < data[p])
			tmp[k++] = data[i++];
		else
			tmp[k++] = data[p++];
	while (i < mid)
		tmp[k++] = data[i++];
	while (p <= high)
		tmp[k++] = data[p++];
	i = low;
	p = 0;
	while (p < k)
		data[i++] = tmp[p++];
}

5、【算法】递归形式的两路归并排序

void mergeSort(int data[], int s, int t) //对data[s…t]进行归并排序
{
	int m;
	if (s < t) {
		m = (s + t) / 2;	//将data[s…t]均分为data[s…m]和data[m+1…t]
		mergeSort(data, s, m);	//递归地对data[s…m]进行归并排序
		mergeSort(data, m + 1, t);	//递归地对data[m+1…t]进行归并排序
		merge(data, s, m + 1, t);	//将data[s…m]和data[m+1…t]归并为data[s…t]
	}
}

6、算法评价

时间复杂度：O(nlog2n)。
空间复杂度： O(n)。
归并排序是一种稳定的排序方法。

七、内部排序方法小节

更多软考的内容：关于软考的博客