CHAPTER 10 Formal Grammars of English
CHAPTER 10 Formal Grammars of English
Speech and Language Processing ed3 读书笔记
This chapter is hard to be condensed. Just read through it.
The word syntax comes from the Greek s y ˊ n t a x i s s\acute{y}ntaxis syˊntaxis, meaning “setting out together or arrangement”, and refers to the way words are arranged together.
10.1 Constituency
The fundamental notion underlying the idea of constituency is that of abstraction — groups of words behaving as a single units, or constituents. A significant part of developing a grammar involves discovering the inventory of constituents present in the language.
10.2 Context-Free Grammars
The most widely used formal system for modeling constituent structure in English and other natural languages is the Context-Free Grammar, or CFG. Context-free grammars are also called Phrase-Structure Grammars, and the formalism is equivalent to Backus-Naur Form, or BNF.
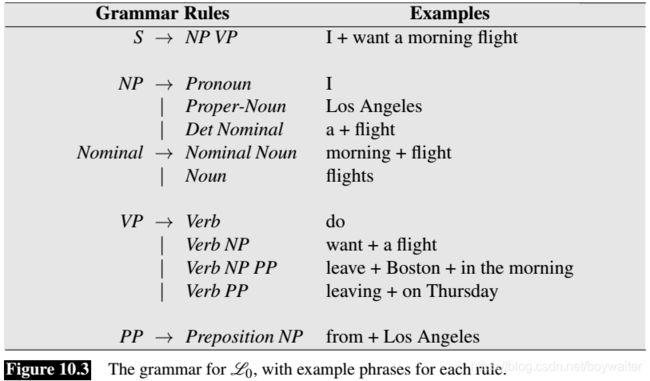
A context-free grammar consists of a set of rules or productions, each of which expresses the ways that symbols of the language can be grouped and ordered together, and a lexicon of words and symbols. For example, the following productions express that an NP (or noun phrase) can be composed of either a ProperNoun or a determiner (Det) followed by a Nominal; a Nominal in turn can consist of one or more Nouns.
N P → D e t N o m i n a l N P → P r o p e r N o u n N o m i n a l → N o u n ∣ N o m i n a l N o u n \begin{aligned} NP &\to Det\ Nominal\\ NP &\to ProperNoun\\ Nominal &\to Noun | Nominal\ Noun\\\end{aligned} NPNPNominal→Det Nominal→ProperNoun→Noun∣Nominal Noun
Context-free rules can be hierarchically embedded, so we can combine the previous rules with others, like the following, that express facts about the lexicon:
D e t → a D e t → t h e N o u n → f l i g h t \begin{aligned} Det &\to a\\ Det &\to the\\ Noun &\to flight\\\end{aligned} DetDetNoun→a→the→flight
The symbols that are used in a CFG are divided into two classes. The symbols that correspond to words in the language (“the”, “nightclub”) are called terminal symbols; the lexicon is the set of rules that introduce these terminal symbols. The symbols that express abstractions over these terminals are called non-terminals. Notice that in the lexicon, the non-terminal associated with each word is its lexical category, or part-of-speech, which we defined in Chapter 8.
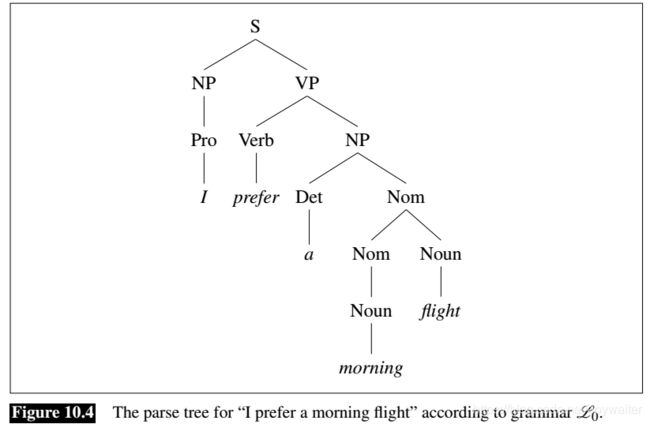
The sequence of rule expansions is called a derivation of the string of words. It is common to represent a derivation by a parse tree (commonly shown inverted with the root at the top). Figure 10.1 shows the tree representation of this derivation.
In the parse tree shown in Fig. 10.1, we can say that the node NP dominates all the nodes in the tree (Det, Nom, Noun, a, flight). We can say further that it immediately dominates the nodes Det and Nom.
The formal language defined by a CFG is the set of strings that are derivable from the designated start symbol. Each grammar must have one designated start symbol, which is often called S.
Figure 10.2 gives a sample lexicon, and Fig. 10.3 summarizes the grammar rules we’ve seen so far, which we’ll call L 0 \mathscr{L}_0 L0.
It is sometimes convenient to represent a parse tree in a more compact format called bracketed notation; here is the bracketed representation of the parse tree of Fig. 10.4:
(10.1) [ S [ N P [ P r o I ] ] [ V P [ V prefer ] [ N P [ D e t a ] [ N o m [ N morning ] [ N o m [ N flight ] ] ] ] ] ] [S [NP [Pro\textrm{ I}]] [VP [V \textrm{ prefer}] [NP [Det \textrm{ a}] [Nom [N \textrm{ morning}] [Nom [N \textrm{ flight}]]]]]] [S[NP[Pro I]][VP[V prefer][NP[Det a][Nom[N morning][Nom[N flight]]]]]]
A CFG like that of L 0 \mathscr{L}_0 L0 defines a formal language. We saw in Chapter 2 that a formal language is a set of strings. Sentences (strings of words) that can be derived by a grammar are in the formal language defined by that grammar, and are called grammatical sentences. Sentences that cannot be derived by a given formal grammar are not in the language defined by that grammar and are referred to as ungrammatical. In linguistics, the use of formal languages to model natural languages is called generative grammar since the language is defined by the set of possible sentences “generated” by the grammar.
10.2.1 Formal Definition of Context-Free Grammar
A context-free grammar G G G is defined by four parameters: N , Σ , R , S N, \Sigma, R, S N,Σ,R,S (technically this is a “4-tuple”).
N N N: a set of non-terminal symbols (or variables)
Σ \Sigma Σ: a set of terminal symbols (disjoint from N N N)
R R R: a set of rules or productions, each of the form A → β A\to \beta A→β , where A A A is a non-terminal, β \beta β is a string of symbols from the infinite set of strings ( Σ ∪ N ) ∗ (\Sigma \cup N)^∗ (Σ∪N)∗
S S S: a designated start symbol and a member of N
For the remainder of the book we adhere to the following conventions when discussing the formal properties of context-free grammars (as opposed to explaining particular facts about English or other languages).
Capital letters like A, B, and S: Non-terminals
S: The start symbol
Lower-case Greek letters like α , β \alpha, \beta α,β, and γ \gamma γ: Strings drawn from ( Σ ∪ N ) ∗ (\Sigma\cup N)∗ (Σ∪N)∗
Lower-case Roman letters like u , v u, v u,v, and w w w: Strings of terminals
A language is defined through the concept of derivation. One string derives another one if it can be rewritten as the second one by some series of rule applications. More formally, following Hopcroft and Ullman (1979),
if A → β A \to \beta A→β is a production of R R R and α \alpha α and γ \gamma γ are any strings in the set ( Σ ∪ N ) ∗ (\Sigma\cup N)∗ (Σ∪N)∗, then we say that α A γ \alpha A\gamma αAγ directly derives α β γ \alpha \beta \gamma αβγ, or α A γ ⇒ α β γ \alpha A\gamma \Rightarrow \alpha \beta \gamma αAγ⇒αβγ.
Derivation is then a generalization of direct derivation:
Let α 1 , α 2 , … , α m \alpha_1,\alpha_2,\ldots, \alpha_m α1,α2,…,αm be strings in ( Σ ∪ N ) ∗ (\Sigma\cup N)∗ (Σ∪N)∗, m ≥ 1 m \ge 1 m≥1, such that
α 1 ⇒ α 2 , α 2 ⇒ α 3 , … , α m − 1 ⇒ α m \alpha_1\Rightarrow \alpha_2,\alpha_2\Rightarrow \alpha_3,\ldots, \alpha_{m-1}\Rightarrow \alpha_m α1⇒α2,α2⇒α3,…,αm−1⇒αm
We say that α 1 \alpha_1 α1 derives α m \alpha_m αm, or α 1 ⇒ α m \alpha_1 \Rightarrow \alpha_m α1⇒αm.
We can then formally define the language L G \mathscr{L}_G LG generated by a grammar G G G as the set of strings composed of terminal symbols that can be derived from the designated start symbol S S S.
L G = { w ∣ w is in Σ ∗ and S ⇒ w } \mathscr{L}_G = \{w|w\textrm{ is in }\Sigma∗ \textrm{ and } S \Rightarrow w\} LG={w∣w is in Σ∗ and S⇒w}
The problem of mapping from a string of words to its parse tree is called syntactic parsing; we define algorithms for parsing in Chapter 11.
10.3 Some Grammar Rules for English
In this section, we introduce a few more aspects of the phrase structure of English; for consistency we will continue to focus on sentences from the ATIS domain. Because of space limitations, our discussion is necessarily limited to highlights. Readers are strongly advised to consult a good reference grammar of English, such as Huddleston and Pullum (2002).
10.3.1 Sentence-Level Constructions
Among the large number of constructions for English sentences, four are particularly common and important: declaratives, imperatives, yes-no questions, and wh-questions.
Sentences with declarative structure have a subject noun phrase followed by a verb phrase, like “I prefer a morning flight”.
Sentences with imperative structure often begin with a verb phrase and have no subject.
S → V P S\to VP S→VP
Sentences with yes-no question structure are often (though not always) used to ask questions; they begin with an auxiliary verb, followed by a subject NP, followed by a VP.
S → A u x N P V P S \to Aux\ NP\ VP S→Aux NP VP
The most complex sentence-level structures we examine here are the various **wh-**structures. These are so named because one of their constituents is a wh-phrase, that is, one that includes a wh-word (who, whose, when, where, what, which, how, why). These may be broadly grouped into two classes of sentence-level structures. The wh-subject-question structure is identical to the declarative structure, except that the first noun phrase contains some wh-word.
S → W h - N P V P S \to Wh\textrm{-}NP\ VP S→Wh-NP VP
In the wh-non-subject-question structure, the wh-phrase is not the subject of the sentence, and so the sentence includes another subject. In these types of sentences the auxiliary appears before the subject NP, just as in the yes-no question structures. Here is an example followed by a sample rule:
What flights do you have from Burbank to Tacoma Washington?
S → W h - N P A u x N P V P S \to Wh\textrm{-}NP\ Aux\ NP\ VP S→Wh-NP Aux NP VP
Constructions like the wh-non-subject-question contain what are called long distance dependencies because the Wh-NP what flights is far away from the predicate that it is semantically related to, the main verb have in the VP. In some models of parsing and understanding compatible with the grammar rule above, long-distance dependencies like the relation between flights and have are thought of as a semantic relation. In such models, the job of figuring out that flights is the argument of have is done during semantic interpretation. In other models of parsing, the relationship between flights and have is considered to be a syntactic relation, and the grammar is modified to insert a small marker called a trace or empty category after the verb. We return to such empty-category models when we introduce the Penn Treebank on page 208.
10.3.2 Clauses and Sentences
Before we move on, we should clarify the status of the S rules in the grammars we just described. S rules are intended to account for entire sentences that stand alone as fundamental units of discourse. However, S can also occur on the right-hand side of grammar rules and hence can be embedded within larger sentences. Clearly then, there’s more to being an S than just standing alone as a unit of discourse.
What differentiates sentence constructions (i.e., the S rules) from the rest of the grammar is the notion that they are in some sense complete. In this way they correspond to the notion of a clause, which traditional grammars often describe as forming a complete thought. One way of making this notion of “complete thought” more precise is to say an S is a node of the parse tree below which the main verb of the S has all of its arguments. We define verbal arguments later, but for now let’s just see an illustration from the tree for I prefer a morning flight in Fig. 10.4 on page 199. The verb prefer has two arguments: the subject I and the object a morning flight. One of the arguments appears below the VP node, but the other one, the subject NP, appears only below the S node (a counter example of complete thought).
10.3.3 The Noun Phrase
Our L 0 \mathscr{L}_0 L0 grammar introduced three of the most frequent types of noun phrases that occur in English: pronouns, proper nouns and the N P → D e t N o m i n a l NP \to\ Det\ Nominal NP→ Det Nominal construction. The central focus of this section is on the last type since that is where the bulk of the syntactic complexity resides. These noun phrases consist of a head, the central noun in the noun phrase, along with various modifiers that can occur before or after the head noun. Let’s take a close look at the various parts.
The Determiner
Noun phrases can begin with simple lexical determiners, as in the following examples:
a stop the flights this flight
those flights any flights some flights
The role of the determiner in English noun phrases can also be filled by more complex expressions, as follows:
United’s flight
United’s pilot’s union
Denver’s mayor’s mother’s canceled flight
In these examples, the role of the determiner is filled by a possessive expression consisting of a noun phrase followed by an ’s as a possessive marker, as in the following rule.
D e t → N P ′ s Det \to\ NP\ 's Det→ NP ′s
The fact that this rule is recursive (since an NP can start with a Det) helps us model the last two examples above, in which a sequence of possessive expressions serves as a determiner.
Under some circumstances determiners are optional in English. For example, determiners may be omitted if the noun they modify is plural:
(10.2) Show me flights from San Francisco to Denver on weekdays
As we saw in Chapter 8, mass nouns also don’t require determination. Recall that mass nouns often (not always) involve something that is treated like a substance (including e.g., water and snow), don’t take the indefinite article “a”, and don’t tend to pluralize. Many abstract nouns are mass nouns (music, homework). Mass nouns in the ATIS domain include breakfast, lunch, and dinner:
(10.3) Does this flight serve dinner?
The Nominal
The nominal construction follows the determiner and contains any pre- and post-head noun modifiers. As indicated in grammar L 0 \mathscr{L}0 L0, in its simplest form a nominal can consist of a single noun.
N o m i n a l → N o u n Nominal \to Noun Nominal→Noun
As we’ll see, this rule also provides the basis for the bottom of various recursive rules used to capture more complex nominal constructions.
Before the Head Noun
A number of different kinds of word classes can appear before the head noun (the “postdeterminers”) in a nominal. These include cardinal numbers (one, two), ordinal numbers (first, second, third, and so on), quantifiers (many, (a) few, several ), and adjectives.
Adjectives can also be grouped into a phrase called an adjective phrase or AP. APs can have an adverb before the adjective (see Chapter 8 for definitions of adjectives and adverbs):
the least expensive fare
After the Head Noun
A head noun can be followed by postmodifiers. Three kinds of nominal postmodifiers are common in English:
prepositional phrases all flights from Cleveland
non-finite clauses any flights arriving after eleven a.m.
relative clauses a flight that serves breakfast
Here are some examples of prepositional phrase postmodifiers, with brackets inserted to show the boundaries of each PP; note that two or more PPs can be strung together within a single NP:
all flights [from Cleveland] [to Newark]
arrival [in San Jose] [before seven p.m.]
a reservation [on flight six oh six] [from Tampa] [to Montreal]
Here’s a new nominal rule to account for postnominal PPs:
N o m i n a l → N o m i n a l P P Nominal \to Nominal\ PP Nominal→Nominal PP
The three most common kinds of non-finite postmodifiers are the gerundive (- ing), -ed, and infinitive forms.
Gerundive postmodifiers are so called because they consist of a verb phrase that begins with the gerundive (-ing) form of the verb. Here are some examples:
any of those [leaving on Thursday]
any flights [arriving after eleven a.m.]
flights [arriving within thirty minutes of each other]
We can define the Nominals with gerundive modifiers as follows, making use of a new non-terminal GerundVP:
N o m i n a l → N o m i n a l G e r u n d V P Nominal \to Nominal\ GerundVP Nominal→Nominal GerundVP
We can make rules for GerundVP constituents by duplicating all of our VP productions, substituting GerundV for V.
G e r u n d V P → G e r u n d V N P ∣ G e r u n d V P P ∣ G e r u n d V ∣ G e r u n d V N P P P GerundVP \to GerundV\ NP |GerundV\ PP |GerundV |GerundV\ NP\ PP GerundVP→GerundV NP∣GerundV PP∣GerundV∣GerundV NP PP
GerundV can then be defined as
G e r u n d V → b e i n g ∣ a r r i v i n g ∣ l e a v i n g ∣ … GerundV \to being |arriving |leaving |\ldots GerundV→being∣arriving∣leaving∣…
The phrases in italics below are examples of the two other common kinds of non-finite clauses, infinitives and -ed forms:
the last flight to arrive in Boston
I need to have dinner served
Which is the aircraft used by this flight?
A postnominal relative clause (more correctly a restrictive relative clause), is a clause that often begins with a relative pronoun (that and who are the most common). The relative pronoun functions as the subject of the embedded verb in the following examples:
a flight that serves breakfast
flights that leave in the morning
the one that leaves at ten thirty five
We might add rules like the following to deal with these:
N o m i n a l → N o m i n a l R e l C l a u s e R e l C l a u s e → ( w h o ∣ t h a t ) V P Nominal \to Nominal\ RelClause\\ RelClause \to (who\ |\ that)\ VP Nominal→Nominal RelClauseRelClause→(who ∣ that) VP
The relative pronoun may also function as the object of the embedded verb, as in the following example.
the earliest American Airlines flight that I can get
Various postnominal modifiers can be combined, as the following examples show:
a flight [from Phoenix to Detroit] [leaving Monday evening]
evening flights [from Nashville to Houston] [that serve dinner]
a friend [living in Denver] [that would like to visit me here in Washington DC]
Before the Noun Phrase
Word classes that modify and appear before NPs are called predeterminers. Many of these have to do with number or amount; a common predeterminer is all:
all the flights all flights all non-stop flights
The example noun phrase given in Fig. 10.5 illustrates some of the complexity that arises when these rules are combined.
10.3.4 The Verb Phrase
The verb phrase consists of the verb and a number of other constituents. In the simple rules we have built so far, these other constituents include NPs and PPs and combinations of the two:
VP → \to → Verb disappear
VP → \to → Verb NP prefer a morning flight
VP → \to → Verb NP PP leave Boston in the morning
VP → \to → Verb PP leaving on Thursday
Verb phrases can be significantly more complicated than this. Many other kinds of constituents, such as an entire embedded sentence, can follow the verb. These are called sentential complements:
You [VP[V said [S you had a two hundred sixty six dollar fare]]
[VP [V Tell] [NP me] [S how to get from the airport in Philadelphia to downtown]]
I [VP [V think [S I would like to take the nine thirty flight]]
Here’s a rule for these:
V P → V e r b S VP\to Verb\ S VP→Verb S
Similarly, another potential constituent of the VP is another VP. This is often the case for verbs like want, would like, try, intend, need:
I want [VP to fly from Milwaukee to Orlando]
Hi, I want [VP to arrange three flights]
While a verb phrase can have many possible kinds of constituents, not every verb is compatible with every verb phrase. For example, the verb want can be used either with an NP complement (I want a flight . . . ) or with an infinitive VP complement (I want to fly to . . . ). By contrast, a verb like find cannot take this sort of VP complement (* I found to fly to Dallas).
This idea that verbs are compatible with different kinds of complements is a very old one; traditional grammar distinguishes between transitive verbs like find, which take a direct object NP (I found a flight), and intransitive verbs like disappear, which do not (*I disappeared a flight).
Where traditional grammars subcategorize verbs into these two categories (transitive and intransitive), modern grammars distinguish as many as 100 subcategories. We say that a verb like find subcategorizes for an NP, and a verb like want subcategorizes for either an NP or a non-finite VP. We also call these constituents the complements of the verb (hence our use of the term sentential complement above). So we say that want can take a VP complement. These possible sets of complements are called the subcategorization frame for the verb. Another way of talking about the relation between the verb and these other constituents is to think of the verb as a logical predicate and the constituents as logical arguments of the predicate. So we can think of such predicate-argument relations as FIND(I, A FLIGHT)} or WANT(I, TO FLY). We talk more about this view of verbs and arguments in Chapter 14 when we talk about predicate calculus representations of verb semantics. Subcategorization frames for a set of example verbs are given in Fig. 10.6.
We can capture the association between verbs and their complements by making separate subtypes of the class Verb (e.g., Verb-with-NP-complement, Verb-with-InfVP-complement, Verb-with-S-complement, and so on):
V e r b - w i t h - N P - c o m p l e m e n t → f i n d ∣ l e a v e ∣ r e p e a t ∣ … V e r b - w i t h - S - c o m p l e m e n t → t h i n k ∣ b e l i e v e ∣ s a y ∣ … V e r b - w i t h - I n f - V P - c o m p l e m e n t → w a n t ∣ t r y ∣ n e e d ∣ … Verb\textrm-with\textrm-NP\textrm-complement \to\ find\ |\ leave\ |\ repeat\ | \ldots \\Verb\textrm-with\textrm-S\textrm-complement \to\ think\ |\ believe\ |\ say\ | \ldots\\ Verb\textrm-with\textrm-Inf\textrm-VP\textrm-complement \to\ want\ |\ try\ |\ need\ | \ldots Verb-with-NP-complement→ find ∣ leave ∣ repeat ∣…Verb-with-S-complement→ think ∣ believe ∣ say ∣…Verb-with-Inf-VP-complement→ want ∣ try ∣ need ∣…
Each VP rule could then be modified to require the appropriate verb subtype:
VP → \to → Verb-with-no-complement disappear
VP → \to → Verb-with-NP-comp NP prefer a morning flight
VP → \to → Verb-with-S-comp S said there were two flights
A problem with this approach is the significant increase in the number of rules and the associated loss of generality.
10.3.5 Coordination
The major phrase types discussed here can be conjoined with conjunctions like and, or, and but to form larger constructions of the same type. For example, a coordinate noun phrase can consist of two other noun phrases separated by a conjunction:
Please repeat [NP [NP the flights] and [NP the costs]]
I need to know [NP [NP the aircraft] and [NP the flight number]]
Here’s a rule that allows these structures:
N P → N P a n d N P NP \to NP\ and\ NP NP→NP and NP
Note that the ability to form coordinate phrases through conjunctions is often used as a test for constituency. Consider the following examples, which differ from the ones given above in that they lack the second determiner.
Please repeat the [Nom [Nom flights] and [Nom costs]]
I need to know the [Nom [Nom aircraft] and [Nom flight number]]
The fact that these phrases can be conjoined is evidence for the presence of the underlying Nominal constituent we have been making use of. Here’s a new rule for this:
N o m i n a l → N o m i n a l a n d N o m i n a l Nominal \to Nominal\ and\ Nominal Nominal→Nominal and Nominal
The following examples illustrate conjunctions involving VPs and Ss.
What flights do you have [VP [VP leaving Denver] and [VP arriving in San Francisco]]
[S [S I’m interested in a flight from Dallas to Washington] and [S I’m also interested in going to Baltimore]]
The rules for VP and S conjunctions mirror the NP one given above.
V P → V P a n d V P S → S a n d S VP \to VP\ and\ VP \\S \to S\ and\ S VP→VP and VPS→S and S
Since all the major phrase types can be conjoined in this fashion, it is also possible to represent this conjunction fact more generally; a number of grammar formalisms such as GPSG ((Gazdar et al., 1985)) do this using metarules such as the following:
X → X a n d X X \to X\ and\ X X→X and X
This metarule simply states that any non-terminal can be conjoined with the same non-terminal to yield a constituent of the same type. Of course, the variable X must be designated as a variable that stands for any non-terminal rather than a nonterminal itself.
10.4 Treebanks
Sufficiently robust grammars consisting of context-free grammar rules can be used to assign a parse tree to any sentence. This means that it is possible to build a corpus where every sentence in the collection is paired with a corresponding parse tree. Such a syntactically annotated corpus is called a treebank.
The Penn Treebank project has produced treebanks from the Brown, Switchboard, ATIS, and Wall Street Journal corpora of English, as well as treebanks in Arabic and Chinese. A number of treebanks use the dependency representation we will introduce in Chapter 13, including many that are part of the Universal Dependencies project (Nivre et al., 2016b).
10.4.1 Example: The Penn Treebank Project
Figure 10.7 shows sentences from the Brown and ATIS portions of the Penn Treebank. Note the formatting differences for the part-of-speech tags; such small differences are common and must be dealt with in processing treebanks. The Penn Treebank part-of-speech tagset was defined in Chapter 8. The use of LISP-style parenthesized notation for trees is extremely common and resembles the bracketed notation we saw earlier in (10.1). For those who are not familiar with it we show a standard node-and-line tree representation in Fig. 10.8.


Figure 10.9 shows a tree from the Wall Street Journal. This tree shows another feature of the Penn Treebanks: the use of traces ( -NONE- \verb|-NONE-| -NONE- nodes) to mark long-distance dependencies or syntactic movement. For example, quotations often follow a quotative verb like say. But in this example, the quotation “We would have to wait until we have collected on those assets” precedes the words he said. An empty S containing only the node -NONE- \verb|-NONE-| -NONE-- marks the position after said where the quotation sentence often occurs. This empty node is marked (in Treebanks II and III) with the index 2, as is the quotation S at the beginning of the sentence. Such co-indexing may make it easier for some parsers to recover the fact that this fronted or topicalized quotation is the complement of the verb said. A similar -NONE- \verb|-NONE-| -NONE- node marks the fact that there is no syntactic subject right before the verb to wait; instead, the subject is the earlier NP We. Again, they are both co-indexed with the index 1.
The Penn Treebank II and Treebank III releases added further information to make it easier to recover the relationships between predicates and arguments. Cer tain phrases were marked with tags indicating the grammatical function of the phrase (as surface subject, logical topic, cleft, non-VP predicates) its presence in particular text categories (headlines, titles), and its semantic function (temporal phrases, locations) (Marcus et al. 1994, Bies et al. 1995). Figure 10.9 shows examples of the -SBJ (surface subject) and -TMP (temporal phrase) tags. Figure 10.8 shows in addition the -PRD tag, which is used for predicates that are not VPs (the one in Fig. 10.8 is an ADJP). We’ll return to the topic of grammatical function when we consider dependency grammars and parsing in Chapter 13.
10.4.2 Treebanks as Grammars
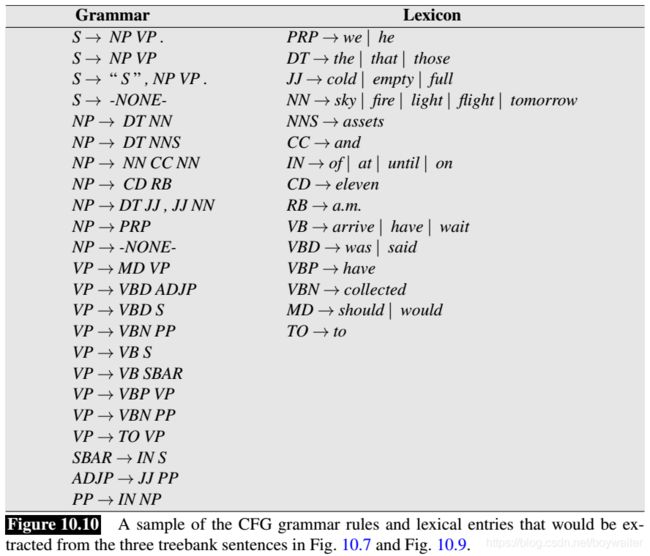
The sentences in a treebank implicitly constitute a grammar of the language represented by the corpus being annotated. For example, from the three parsed sentences in Fig. 10.7 and Fig. 10.9, we can extract each of the CFG rules in them. For simplicity, let’s strip off the rule suffixes (-SBJ and so on). The resulting grammar is shown in Fig. 10.10.
The grammar used to parse the Penn Treebank is relatively flat, resulting in very many and very long rules. For example, among the approximately 4,500 different rules for expanding VPs are separate rules for PP sequences of any length and every possible arrangement of verb arguments:
V P → V B D P P V P → V B D P P P P V P → V B D P P P P P P V P → V B D P P P P P P P P V P → V B A D V P P P V P → V B P P A D V P V P → A D V P V B P P VP \to VBD\ PP \\ VP \to VBD\ PP\ PP \\ VP \to VBD\ PP\ PP\ PP\\ VP \to VBD\ PP\ PP\ PP\ PP\\ VP \to VB\ ADVP\ PP\\ VP \to VB\ PP\ ADVP\\ VP \to ADVP\ VB\ PP\\ VP→VBD PPVP→VBD PP PPVP→VBD PP PP PPVP→VBD PP PP PP PPVP→VB ADVP PPVP→VB PP ADVPVP→ADVP VB PP
as well as even longer rules, such as
V P → V B P P P P P P P P P P P A D V P P P VP \to VBP\ PP\ PP\ PP\ PP\ PP\ ADVP\ PP VP→VBP PP PP PP PP PP ADVP PP
which comes from the VP marked in italics:
This mostly happens because we go from football in the fall to lifting in the winter to football again in the spring.
Some of the many thousands of NP rules include
N P → D T J J N N N P → D T J J N N S N P → D T J J N N N N N P → D T J J J J N N N P → D T J J C D N N S N P → R B D T J J N N N N N P → R B D T J J J J N N S N P → D T J J J J N N P N N S N P → D T N N P N N P N N P N N P J J N N N P → D T J J N N P C C J J J J N N N N S N P → R B D T J J S N N N N S B A R N P → D T V B G J J N N P N N P C C N N P N P → D T J J N N S , N N S C C N N N N S N N N P → D T J J J J V B G N N N N P N N P F W N N P N P → N P J J , J J ‘ ‘ S B A R ’ ’ N N S \begin{aligned} NP &\to\ DT\ JJ\ NN\\ NP &\to\ DT\ JJ\ NNS\\ NP &\to\ DT\ JJ\ NN\ NN\\ NP &\to\ DT\ JJ\ JJ\ NN\\ NP &\to\ DT\ JJ\ CD\ NNS\\ NP &\to\ RB\ DT\ JJ\ NN\ NN\\ NP &\to\ RB\ DT\ JJ\ JJ\ NNS\\ NP &\to\ DT\ JJ\ JJ\ NNP\ NNS\\ NP &\to\ DT\ NNP\ NNP\ NNP\ NNP\ JJ\ NN\\ NP &\to\ DT\ JJ\ NNP\ CC\ JJ\ JJ\ NN\ NNS\\ NP &\to\ RB\ DT\ JJS\ NN\ NN\ SBAR\\ NP &\to\ DT\ VBG\ JJ\ NNP\ NNP\ CC\ NNP\\ NP &\to\ DT\ JJ\ NNS\ ,\ NNS\ CC\ NN\ NNS\ NN\\ NP &\to\ DT\ JJ\ JJ\ VBG\ NN\ NNP\ NNP\ FW\ NNP\\ NP &\to\ NP\ JJ\ ,\ JJ\ ‘‘\ SBAR\ ’ ’\ NNS\\ \end{aligned} NPNPNPNPNPNPNPNPNPNPNPNPNPNPNP→ DT JJ NN→ DT JJ NNS→ DT JJ NN NN→ DT JJ JJ NN→ DT JJ CD NNS→ RB DT JJ NN NN→ RB DT JJ JJ NNS→ DT JJ JJ NNP NNS→ DT NNP NNP NNP NNP JJ NN→ DT JJ NNP CC JJ JJ NN NNS→ RB DT JJS NN NN SBAR→ DT VBG JJ NNP NNP CC NNP→ DT JJ NNS , NNS CC NN NNS NN→ DT JJ JJ VBG NN NNP NNP FW NNP→ NP JJ , JJ ‘‘ SBAR ’’ NNS
The last two of those rules, for example, come from the following two noun phrases:
[DT The] [JJ state-owned] [JJ industrial] [VBG holding] [NN company] [NNP Instituto]
[NNP Nacional] [FW de] [NNP Industria]
[NP Shearson’s] [JJ easy-to-film], [JJ black-and-white] “[SBAR Where We Stand]”
[NNS commercials]
Viewed as a large grammar in this way, the Penn Treebank III Wall Street Journal corpus, which contains about 1 million words, also has about 1 million non-lexical rule tokens, consisting of about 17,500 distinct rule types.
Various facts about the treebank grammars, such as their large numbers of flat rules, pose problems for probabilistic parsing algorithms. For this reason, it is common to make various modifications to a grammar extracted from a treebank. We discuss these further in Chapter 12.
10.4.3 Heads and Head Finding
We suggested informally earlier that syntactic constituents could be associated with a lexical head; N is the head of an NP, V is the head of a VP. The head is the word in the phrase that is grammatically the most important. Heads are passed up the parse tree; thus, each non-terminal in a parse tree is annotated with a single word, which is its lexical head.
Figure 10.11 shows an example of such a tree from Collins (1999), in which each non-terminal is annotated with its head.
For the generation of such a tree, each CFG rule must be augmented to identify one right-side constituent to be the head daughter. The headword for a node is then set to the headword of its head daughter. Choosing these head daughters is simple for textbook examples (NN is the head of NP) but is complicated and indeed controversial for most phrases. (Should the complementizer to or the verb be the head of an infinite verb-phrase?) Modern linguistic theories of syntax generally include a component that defines heads (see, e.g., (Pollard and Sag, 1994)).
An alternative approach to finding a head is used in most practical computational systems. Instead of specifying head rules in the grammar itself, heads are identified dynamically in the context of trees for specific sentences. In other words, once a sentence is parsed, the resulting tree is walked to decorate each node with the appropriate head. Most current systems rely on a simple set of hand-written rules, such as a practical one for Penn Treebank grammars given in Collins (1999) but developed originally by Magerman (1995). For example, the rule for finding the head of an NP is as follows (Collins, 1999, p. 238):
- If the last word is tagged POS, return last-word.
- Else search from right to left for the first child which is an NN, NNP, NNPS, NX, POS, or JJR.
- Else search from left to right for the first child which is an NP.
- Else search from right to left for the first child which is a $, ADJP, or PRN.
- Else search from right to left for the first child which is a CD.
- Else search from right to left for the first child which is a JJ, JJS, RB or QP.
- Else return the last word
Selected other rules from this set are shown in Fig. 10.12. For example, for VP rules of the form V P → Y 1 ⋯ Y n VP \to Y_1 \cdots Y_n VP→Y1⋯Yn, the algorithm would start from the left of Y 1 ⋯ Y n Y_1 \cdots Y_n Y1⋯Yn looking for the first Y i Y_i Yi of type TO; if no TOs are found, it would search for the first Y i Y_i Yi of type VBD; if no VBDs are found, it would search for a VBN, and so on. See Collins (1999) for more details.
10.5 Grammar Equivalence and Normal Form
A formal language is defined as a (possibly infinite) set of strings of words. This suggests that we could ask if two grammars are equivalent by asking if they generate the same set of strings. In fact, it is possible to have two distinct context-free grammars generate the same language.
We usually distinguish two kinds of grammar equivalence: weak equivalence and strong equivalence. Two grammars are strongly equivalent if they generate the same set of strings and if they assign the same phrase structure to each sentence (allowing merely for renaming of the non-terminal symbols). Two grammars are weakly equivalent if they generate the same set of strings but do not assign the same phrase structure to each sentence.
It is sometimes useful to have a normal form for grammars, in which each of the productions takes a particular form. For example, a context-free grammar is in Chomsky normal form (CNF) (Chomsky, 1963) if it is ϵ \epsilon ϵ-free and if in addition each production is either of the form A → B C A \to B\ C A→B C or A → a A \to a A→a. That is, the right-hand side of each rule either has two non-terminal symbols or one terminal symbol. Chomsky normal form grammars are binary branching, that is they have binary trees (down to the prelexical nodes). We make use of this binary branching property in the CKY parsing algorithm in Chapter 11.
Any context-free grammar can be converted into a weakly equivalent Chomsky normal form grammar. For example, a rule of the form
A → B C D A \to B\ C\ D A→B C D
can be converted into the following two CNF rules:
A → B X X → C D A \to B\ X\\ X \to C\ D A→B XX→C D
Sometimes using binary branching can actually produce smaller grammars. For example, the sentences that might be characterized as
VP -> VBD NP PP* \verb|VP -> VBD NP PP*| VP -> VBD NP PP*
are represented in the Penn Treebank by this series of rules:
VP -> VBD NP PP \verb|VP -> VBD NP PP| VP -> VBD NP PP
VP -> VBD NP PP PP \verb|VP -> VBD NP PP PP| VP -> VBD NP PP PP
VP -> VBD NP PP PP PP \verb|VP -> VBD NP PP PP PP| VP -> VBD NP PP PP PP
VP -> VBD NP PP PP PP PP \verb|VP -> VBD NP PP PP PP PP| VP -> VBD NP PP PP PP PP
⋯ \cdots ⋯
but could also be generated by the following two-rule grammar:
VP -> VBD NP PP \verb|VP -> VBD NP PP| VP -> VBD NP PP
VP -> VP PP \verb|VP -> VP PP| VP -> VP PP
The generation of a symbol A with a potentially infinite sequence of symbols B with a rule of the form A → A B A \to A\ B A→A B is known as Chomsky-adjunction.
10.6 Lexicalized Grammars
The approach to grammar presented thus far emphasizes phrase-structure rules while minimizing the role of the lexicon. However, as we saw in the discussions of agreement, subcategorization, and long distance dependencies, this approach leads to solutions that are cumbersome at best, yielding grammars that are redundant, hard to manage, and brittle. To overcome these issues, numerous alternative approaches have been developed that all share the common theme of making better use of the lexicon. Among the more computationally relevant approaches are Lexical-Functional Grammar (LFG) (Bresnan, 1982), Head-Driven Phrase Structure Grammar (HPSG) (Pollard and Sag, 1994), Tree-Adjoining Grammar (TAG) (Joshi, 1985), and Combinatory Categorial Grammar (CCG). These approaches differ with respect to how lexicalized they are — the degree to which they rely on the lexicon as opposed to phrase structure rules to capture facts about the language.
10.6.1 Combinatory Categorial Grammar
In this section, we provide an overview of categorial grammar (Ajdukiewicz 1935, Bar-Hillel 1953), an early lexicalized grammar model, as well as an important modern extension, combinatory categorial grammar, or CCG (Steedman 1996, Steed man 1989, Steedman 2000).
The categorial approach consists of three major elements: a set of categories, a lexicon that associates words with categories, and a set of rules that govern how categories combine in context.
Categories
Categories are either atomic elements or single-argument functions that return a category as a value when provided with a desired category as argument. More formally, we can define C \mathscr{C} C , a set of categories for a grammar as follows:
- A ⊆ C \mathscr{A\subseteq C} A⊆C , where A \mathscr{A} A is a given set of atomic elements
- ( X / Y ) , ( X \ Y ) ∈ C (X/Y), (X\backslash Y) \in \mathscr{C} (X/Y),(X\Y)∈C , if X , Y ∈ C X, Y \in \mathscr{C} X,Y∈C
The slash notation shown here is used to define the functions in the grammar. It specifies the type of the expected argument, the direction it is expected be found, and the type of the result. Thus, ( X / Y ) (X/Y) (X/Y) is a function that seeks a constituent of type Y to its right and returns a value of X; ( X \ Y ) (X\backslash Y) (X\Y) is the same except it seeks its argument to the left.
The set of atomic categories is typically very small and includes familiar elements such as sentences and noun phrases. Functional categories include verb phrases and complex noun phrases among others.
The Lexicon
The lexicon in a categorial approach consists of assignments of categories to words. These assignments can either be to atomic or functional categories, and due to lexical ambiguity words can be assigned to multiple categories. Consider the following sample lexical entries.
flight : N
Miami : NP
cancel : (S\NP)/NP
Nouns and proper nouns like flight and Miami are assigned to atomic categories, reflecting their typical role as arguments to functions. On the other hand, a transitive verb like cancel is assigned the category (S\NP)/NP : a function that seeks an NP on its right and returns as its value a function with the type (S\NP). This function can, in turn, combine with an NP on the left, yielding an S as the result. This captures the kind of subcategorization information discussed in Section 10.3.4, however here the information has a rich, computationally useful, internal structure.
Ditransitive verbs like give, which expect two arguments after the verb, would have the category ((S\NP)/NP)/NP: a function that combines with an NP on its right to yield yet another function corresponding to the transitive verb (S\NP)/NP category such as the one given above for cancel.
Rules
The rules of a categorial grammar specify how functions and their arguments combine. The following two rule templates constitute the basis for all categorial grammars.
X / Y Y ⇒ X X/Y\ Y\Rightarrow X X/Y Y⇒X
Y X \ Y ⇒ X Y\ X\backslash Y \Rightarrow X Y X\Y⇒X
The first rule applies a function to its argument on the right, while the second looks to the left for its argument. We’ll refer to the first as forward function application, and the second as backward function application. The result of applying either of these rules is the category specified as the value of the function being applied.
Given these rules and a simple lexicon, let’s consider an analysis of the sentence United serves Miami. Assume that serves is a transitive verb with the category (S\NP)/NP and that United and Miami are both simple NPs. Using both forward and backward function application, the derivation would proceed as follows:
U n i t e d s e r v e s M i a m ‾ ‾ ‾ N P ( S \ N P ) / N P N P ‾ > S \ N P ‾ < S United\verb| | serves\verb| | Miam\\ \overline{\verb| |}\verb| | \overline{\verb| |}\verb| |\ \overline{\verb| |}\\ NP\verb| |(S\backslash NP)/NP\verb| | NP\\ \verb| |\overline{ \verb| |}>\\ \verb| |S\backslash NP\\ \overline{ \verb| |}<\\S\\ %\rule{100mm}{0.1mm} United serves Miam NP (S\NP)/NP NP > S\NP <S
Categorial grammar derivations are illustrated growing down from the words, rule applications are illustrated with a horizontal line that spans the elements involved, with the type of the operation indicated at the right end of the line. In this example, there are two function applications: one forward function application indicated by the > that applies the verb serves to the NP on its right, and one backward function application indicated by the < that applies the result of the first to the NP United on its left.
With the addition of another rule, the categorial approach provides a straightforward way to implement the coordination metarule described earlier on page 207. Recall that English permits the coordination of two constituents of the same type, resulting in a new constituent of the same type. The following rule provides the mechanism to handle such examples.
X C O N J X ⇒ X X\ CONJ\ X\Rightarrow X X CONJ X⇒X
This rule states that when two constituents of the same category are separated by a constituent of type CONJ they can be combined into a single larger constituent of the same type. The following derivation illustrates the use of this rule.
W e f l e w t o G e n e v a a n d d r o v e t o C h a m o n i x ‾ ‾ ‾ ‾ ‾ ‾ ‾ ‾ N P ( S \ N P ) / P P P P / N P N P C O N J ( S \ N P ) / P P P P / N P N P ‾ > ‾ > P P P P ‾ > ‾ > S \ N P S \ N P ‾ < Φ > S \ N P ‾ < S \verb| |We\verb| | flew\verb| | to\verb| | Geneva\verb| | and\verb| | drove\verb| | to\verb| | Chamonix\\ \verb| |\overline{\verb| |}\verb| |\overline{\verb| |}\verb| |\overline{\verb| |}\verb| |\overline{\verb| |}\verb| |\overline{\verb| |}\verb| |\overline{\verb| |}\verb| |\overline{\verb| |}\verb| |\overline{\verb| |}\\ NP\verb| |(S\backslash NP)/PP\verb| |PP/NP\verb| | NP\verb| | CONJ\verb| | (S\backslash NP)/PP\verb| |PP/NP\verb| |NP\\ \verb| |\overline{\verb| |}>\verb| |\overline{\verb| |}>\\ \verb| |PP\verb| |PP\\ \verb| |\overline{\verb| |}>\verb| |\overline{\verb| |}>\\ \verb| |S\backslash NP\verb| |S\backslash NP\\ \verb| |\overline{\verb| |}<\Phi>\\ S\backslash NP\\ \verb| |\overline{\verb| |}<\\ S\\ We flew to Geneva and drove to Chamonix NP (S\NP)/PP PP/NP NP CONJ (S\NP)/PP PP/NP NP > > PP PP > > S\NP S\NP <Φ>S\NP <S
Here the two S\NP constituents are combined via the conjunction operator < Φ > <\Phi> <Φ> to form a larger constituent of the same type, which can then be combined with the subject NP via backward function application.
These examples illustrate the lexical nature of the categorial grammar approach. The grammatical facts about a language are largely encoded in the lexicon, while the rules of the grammar are boiled down to a set of three rules. Unfortunately, the basic categorial approach does not give us any more expressive power than we had with traditional CFG rules; it just moves information from the grammar to the lexicon. To move beyond these limitations CCG includes operations that operate over functions.
The first pair of operators permit us to compose adjacent functions.
X / Y Y / Z ⇒ X / Z X/Y\ Y/Z\Rightarrow X/Z X/Y Y/Z⇒X/Z
Y \ Z X \ Y ⇒ X \ Z Y\backslash Z\ X\backslash Y \Rightarrow X\backslash Z Y\Z X\Y⇒X\Z
The first rule, called forward composition, can be applied to adjacent constituents where the first is a function seeking an argument of type Y to its right, and the second is a function that provides Y as a result. This rule allows us to compose these two functions into a single one with the type of the first constituent and the argument of the second. Although the notation is a little awkward, the second rule, backward composition is the same, except that we’re looking to the left instead of to the right for the relevant arguments. Both kinds of composition are signaled by a B in CCG diagrams, accompanied by a < or > to indicate the direction.
The next operator is type raising. Type raising elevates simple categories to the status of functions. More specifically, type raising takes a category and converts it to function that seeks as an argument a function that takes the original category as its argument. The following schema show two versions of type raising: one for arguments to the right, and one for the left.
X ⇒ T / ( T \ X ) X \Rightarrow T/(T\backslash X) X⇒T/(T\X)
X ⇒ T \ ( T / X ) X \Rightarrow T\backslash(T/ X) X⇒T\(T/X)
The category T in these rules can correspond to any of the atomic or functional categories already present in the grammar.
A particularly useful example of type raising transforms a simple NP argument in subject position to a function that can compose with a following VP. To see how this works, let’s revisit our earlier example of United serves Miami. Instead of classifying United as an NP which can serve as an argument to the function attached to serve, we can use type raising to reinvent it as a function in its own right as follows.
N P ⇒ S / ( S \ N P ) NP \Rightarrow S/(S\backslash NP) NP⇒S/(S\NP)
Combining this type-raised constituent with the forward composition rule permits the following alternative to our previous derivation. *
U n i t e d s e r v e s M i a m ‾ ‾ ‾ N P ( S \ N P ) / N P N P ‾ > T S / ( S \ N P ) ‾ > B S / N P ‾ > S \verb| |United\verb| | serves\verb| | Miam\\ \overline{\verb| |}\verb| | \overline{\verb| |}\verb| |\ \overline{\verb| |}\\ \verb| |NP\verb| |(S\backslash NP)/NP\verb| | NP\\ \overline{\verb| |}>\textbf{T}\verb| |\\ S/(S\backslash NP)\verb| |\\ \overline{ \verb| |}>\textbf{B}\verb| |\\ S/NP\verb| |\\ \overline{ \verb| |}>\verb| |\\ S\verb| |\\ United serves Miam NP (S\NP)/NP NP >T S/(S\NP) >B S/NP > S
where T \textbf{T} T stands for type raising, and B \textbf{B} B for backward composition.
By type raising United to S / ( S \ N P ) S/(S\backslash NP) S/(S\NP), we can compose it with the transitive verb serves to yield the ( S / N P ) (S/NP) (S/NP) function needed to complete the derivation.
There are several interesting things to note about this derivation. First, is it provides a left-to-right, word-by-word derivation that more closely mirrors the way humans process language. This makes CCG a particularly apt framework for psycholinguistic studies. Second, this derivation involves the use of an intermediate unit of analysis, United serves, that does not correspond to a traditional constituent in English. This ability to make use of such non-constituent elements provides CCG with the ability to handle the coordination of phrases that are not proper constituents, as in the following example.
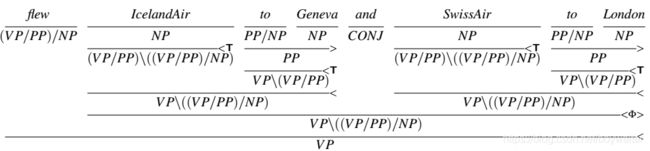
(10.11) We flew IcelandAir to Geneva and SwissAir to London.
Here, the segments that are being coordinated are IcelandAir to Geneva and SwissAir to London, phrases that would not normally be considered constituents, as can be seen in the following standard derivation for the verb phrase flew IcelandAir to Geneva.
f l e w I c e l a n d A i r t o G e n e v a ‾ ‾ ‾ ‾ ( V P / P P ) / N P N P P P / N P N P ‾ > ‾ > V P / N P P P ‾ > V P \verb| |flew\verb| | IcelandAir\verb| | to\verb| | Geneva\\ \overline{\verb| |}\verb| | \overline{\verb| |}\verb| |\ \overline{\verb| |}\verb| | \overline{\verb| |}\\ \verb||(VP/PP)/NP\verb| |NP\verb| | PP/NP\verb| |NP\verb| | \\ \overline{ \verb| |}>\overline{ \verb| |}>\verb| |\\ \verb| |VP/NP\verb| |PP\verb| |\\ \overline{ \verb| |}>\verb| |\\ VP\verb| |\\ flew IcelandAir to Geneva (VP/PP)/NP NP PP/NP NP > > VP/NP PP > VP
In this derivation, there is no single constituent that corresponds to IcelandAir to Geneva, and hence no opportunity to make use of the < Φ > <\Phi> <Φ> operator. Note that complex CCG categories can get a little cumbersome, so we’ll use VP as a shorthand for ( S \ N P ) (S\backslash NP) (S\NP) in this and the following derivations.
The following alternative derivation provides the required element through the use of both backward type raising and backward function composition.
Applying the same analysis to SwissAir to London satisfies the requirements for the < Φ > <\Phi> <Φ> operator, yielding the following derivation for our original example.
Finally, let’s examine how these advanced operators can be used to handle long-distance dependencies (also referred to as syntactic movement or extraction). As mentioned in Section 10.3.1, long-distance dependencies arise from many English constructions including wh-questions, relative clauses, and topicalization. What these constructions have in common is a constituent that appears somewhere distant from its usual, or expected, location. Consider the following relative clause as an example.
the flight that United diverted
Here, divert is a transitive verb that expects two NP arguments, a subject NP to its left and a direct object NP to its right; its category is therefore ( S \ N P ) / N P (S\backslash NP)/NP (S\NP)/NP. However, in this example the direct object the flight has been “moved” to the beginning of the clause, while the subject United remains in its normal position. What is needed is a way to incorporate the subject argument, while dealing with the fact that the flight is not in its expected location.
The following derivation accomplishes this, again through the combined use of type raising and function composition.
As we saw with our earlier examples, the first step of this derivation is type raising United to the category S / ( S \ N P ) S/(S\backslash NP) S/(S\NP) allowing it to combine with diverted via forward composition. The result of this composition is S/NP which preserves the fact that we are still looking for an NP to fill the missing direct object. The second critical piece is the lexical category assigned to the word that: ( N P \ N P ) / ( S / N P ) (NP\backslash NP)/(S/NP) (NP\NP)/(S/NP). This function seeks a verb phrase missing an argument to its right, and transforms it into an NP seeking a missing element to its left, precisely where we find the flight.
CCGBank
As with phrase-structure approaches, treebanks play an important role in CCG-based approaches to parsing. CCGBank (Hockenmaier and Steedman, 2007) is the largest and most widely used CCG treebank. It was created by automatically translating phrase-structure trees from the Penn Treebank via a rule-based approach. The method produced successful translations of over 99% of the trees in the Penn Treebank resulting in 48,934 sentences paired with CCG derivations. It also provides a lexicon of 44,000 words with over 1200 categories. Chapter 12 will discuss how these resources can be used to train CCG parsers.
10.7 Summary
This chapter has introduced a number of fundamental concepts in syntax through the use of context-free grammars.
- In many languages, groups of consecutive words act as a group or a constituent, which can be modeled by context-free grammars (which are also known as phrase-structure grammars).
- A context-free grammar consists of a set of rules or productions, expressed over a set of non-terminal symbols and a set of terminal symbols. Formally, a particular context-free language is the set of strings that can be derived from a particular context-free grammar.
- A generative grammar is a traditional name in linguistics for a formal language that is used to model the grammar of a natural language.
- There are many sentence-level grammatical constructions in English; declarative, imperative, yes-no question, and wh-question are four common types; these can be modeled with context-free rules.
- An English noun phrase can have determiners, numbers, quantifiers, and adjective phrases preceding the head noun, which can be followed by a number of postmodifiers; gerundive VPs, infinitives VPs, and past participial VPs are common possibilities.
- Subjects in English agree with the main verb in person and number.
- Verbs can be subcategorized by the types of complements they expect. Simple subcategories are transitive and intransitive; most grammars include many more categories than these.
- Treebanks of parsed sentences exist for many genres of English and for many languages. Treebanks can be searched with tree-search tools.
- Any context-free grammar can be converted to Chomsky normal form, in which the right-hand side of each rule has either two non-terminals or a single terminal.
- Lexicalized grammars place more emphasis on the structure of the lexicon, lessening the burden on pure phrase-structure rules.
- Combinatorial categorial grammar (CCG) is an important computationally relevant lexicalized approach.